Множественная регрессия и корреляция.Спецификация модели множественной регрессии

Тема 4. Множественная регрессия и корреляция

4.1. Спецификация модели множественной регрессии 4.2. Оценка параметров уравнения множествен-ной регрессии 4.3. Множественная корреляция 4.4. Оценка надежности результатов множествен-ной регрессии и корреляции 4.5. Предпосылки метода наименьших квадратов и обобщенный МНК

4.1. Спецификация модели множественной регрессии

Спецификация модели – обоснованный с позиций экономической теории выбор вида и структуры модели, отбор факторов и математическое описание характера их влияния на результирующий признак

Множественная регрессия

Если при построении эконометрической модели не удается выявить единственный фактор, оказывающий доминирующее влияние на исследуемый результативный признак, то вместо парной регрессии применяют множественную регрессию. Множественная регрессия – это уравнение связи зависимой переменной с несколькими независимыми переменными: y = f ( x1, x2, … , xm, e ), где y - зависимая переменная (результативный признак); x1, x2, … , xm - независимые переменные (факторы); e - случайная величина (остаток). Спецификация модели множественной регрессии включает выбор вида функции регрессии и отбор факторов.

Функции множественной регрессии

Для построения модели множественной регрессии чаще используются следующие функции: ·  линейная y = a + b1 * x1 + b2 * x2 + … + bm * xm + e ;   ·  степенная   ·  экспонента   ·  гипербола   ·  полином y = a + b1* x1 + b2* x2 + b3* x12 + b4 * x22 + b5*x1*x2 + e Можно использовать и другие функции, приводимые к линейному виду. Однако, при этом число наблюдений должно не менее, чем в 6 – 8 раз превышать число факторов и модель должна быть экономически интерпретируемой.

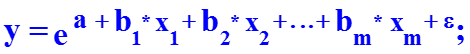
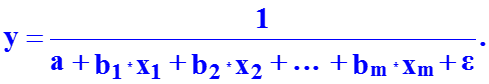
Производственная функция

Степенная модель множественной регрессии применяется в производственных функциях вида : где P – количество продукта, изготавливаемого с помощью m производственных факторов объемом F1, F2, …, Fm; bi – эластичность количества продукции по отношению к объему i-го производственного фактора. Коэффициенты bi показывают, на сколько процентов изменяется результат с изменением соответствующего фактора на 1 процент. Сумма bi характеризует общую эластичность выпуска продукции, т.е. процент увеличения выпуска продукции при возрастании объема каждого фактора на 1 процент.

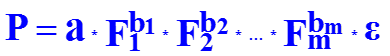
Стандартизованное уравнение линейной регрессии

В ряде случаев применяют линейное уравнение регрессии в стандартизованном масштабе: где - стандартизованные переменные; bi – стандартизованные коэффициенты регрессии. Коэффициенты bi позволяют ранжировать факторы по силе их влияния на результативный признак. Связь коэффи-циентов множественной регрессии bi со стандартизованными коэффициентами bi описывается соотношением Параметр a определяется как

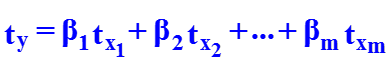
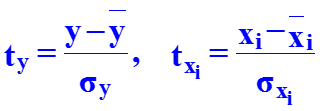
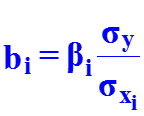
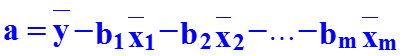
Примеры множественной линейной регрессии

Расходы семьи на продукты питания y в зависимости от дохода на одного члена семьи x1 и размера семьи x2: y = a + b1 * x1 + b2 * x2 + e Уровень потребления в текущем периоде Ct в зависимости от дохода того же периода Rt и от дохода предшествующего периода Rt-1 : Ct = a + b0 * Rt + b1 * Rt-1 + e , b0 - краткосрочная предельная склонность к потреблению, b = b0 + b1 - долгосрочная склонность к потреблению. Функция потребления может рассматриваться также в зависимости от предыдущего уровня потребления Ct-1: Ct = a + b0 * Rt + b1 * Ct-1 + e , долгосрочная склонность к потреблению здесь равна:

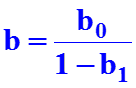
8

Фиктивные переменные для качественных факторов

Факторы должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, то каждому его уровню следует тем или иным способом придать количественную определенность. С этой целью применяются фиктивные переменные. Если качественный фактор имеет два различимых уровня, то вводится одна фиктивная переменная Z, значения которой устанавливаются равными:

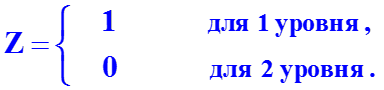
Если качественный фактор имеет три уровня, то вводятся две фиктивные переменные Z1 и Z2, значения которых устанавливаются равными:

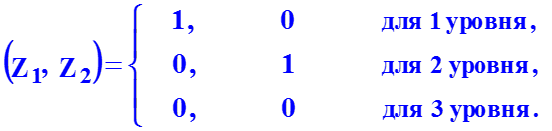
Фиктивная переменная для качественного фактора с 2 уровнями

Факторы должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, то каждому его уровню следует тем или иным способом придать количественную определенность. С этой целью применяются фиктивные переменные. Если качественный фактор имеет два различимых уровня с n1 и n2 наблю-дениями, то вводится одна фиктивная переменная

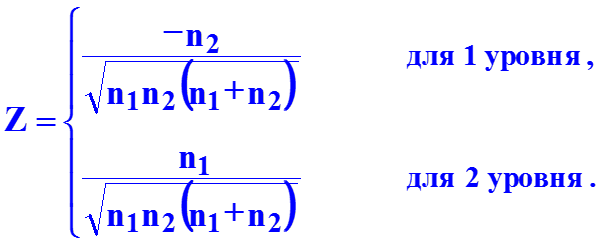
Можно использовать значение 0 для первого уровня и 1 для второго уровня (или, наоборот).

Фиктивные переменные для качественного фактора с 3 уровнями