Многомерные процессы. Коинтеграция.Векторная авторегрессия

факторизуется в произведение прямоугольных матриц, и вторая из них дает коинтегрирующий вектор.

Наконец, при равенстве собственных чисел может тем не менее существовать два линейно независимых собственных вектора, соответствующих этому собственному числу. В этом случае матрицы  и П приводятся к диагональной форме, и система уравнении для вектора  принимает вид: , . Обе компоненты относятся к типу I(1) , поэтому обе компоненты вектора  также относятся к типу I(1) , а коинтегрирующей комбинации нет. Заметим, что матрица П в этом случае состоит из одних нулей, и ее ранг равен 0.

Теперь рассмотрим случай модели VAR(1) для трехмерного случайного вектора, матрица  имеет 3 собственных числа, и набор возможностей несколько расщиряется. Начнем со случая, когда , ,  и . Тогда матрица с из собственных векторов существует, и система уравнений для компонент вектора  распадается на отдельные уравнения:

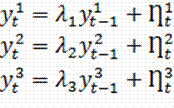
Очевидно, что третья компонента будет типа I(1) , а две остальные — типа I(0). Поэтому все компоненты вектора , будут типа I(1) , в то же время две их линейные комбинации, соответствующие переменным  и  будут стационарными. Это означает, что переменные , ,  коинтегрированы, и существует два линейно независимых коинтегрирующих вектора. Эти два вектора определяют линейное подпространство, каждый элемент которого будет коинтегрирующим вектором. Эта ситуация препятствует непосредственной интерпретации коинтегрирующих векторов как долгосрочных зависимостей между переменными, ведь теперь таких соотношений бесконечно много.

Ранг матрицы П равен 2 и вновь совпадает с числом линеино независимых коинтегрирующих векторов. Ничего принципиально не меняет случай, когда . В этом случае  по-прежнему процесс типа I(1),  — типа I(0) , а  определяется моделью ADL(1,1) и также является стационарным, т.е. Типа I(0). Все компоненты вектора  являются процессами типа I(1) , а переменные  и  являются стационарными линейно независимыми комбинациями компонент вектора , т.е. существует два линейно независимых коинтегрирующих вектора.

Матрица П легко приводится либо к диагональному виду:

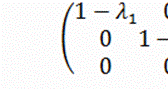, либо к виду 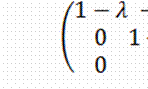, что дает соответственно

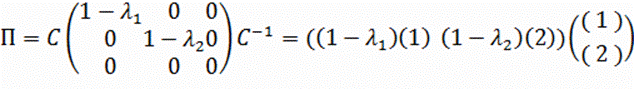
либо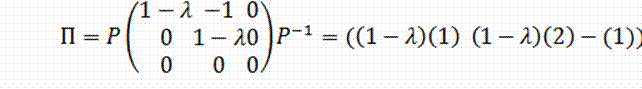

Через (1) и (2) - обозначены первый и второй столбцы матрицы  или , а через ( 1 ) и ( 2 ) — соответствующие строки матрицы  или . В обоих случаях матрица П разложена в произведение прямоугольных матриц размерностью (n х r) и (r x n) соответственно, где n — размерность вектора , а r — ранг матрицы П. При этом строки второй из матриц являются коинтегрирующими векторами. В литературе почему-то принято обозначать эти матрицы строчными греческими буквами α и , и факторизация записывается в виде .

Теперь рассмотрим случай, когда , а . Если при этом кратному собственному числу  соответствует только один собственный вектор, то система уравнений для вектора  принимает вид:

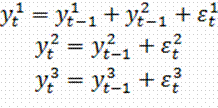
Очевидно, что , , . Все компоненты вектора  относятся тогда к типу I(2) , и существуют две коинтегрирующие линейные комбинации. Одна из них, соответствующая ‚ понижает порядок интеграции до 1, а вторая, соответствующая , понижает порядок до 0. Ранг матрицы П равен 2, ее факторизация в виде  опять имеет место.

Если же кратному единичному собственному значению соответствует два линейно независимых собственных вектора, то VAR-модель для вектора  распадается на уравнения для отдельных компонент.

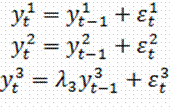
Тогда , ,. Компоненты вектора  будут процессами типа I(1), и существует лищь одна коинтегрирующая комбинация, соответствующая . Ранг матрицы П равен 1, и она может быть представлена в виде произведения вектора-столбца на вектор-строку, которая и является коинтегрирующим вектором.

Осталось рассмотреть случай, когда . Этому трехкратному собственному числу может соответствовать один, два или три линейно независимых собственных вектора. Если такой вектор один, то для вектора  получается следующая система:

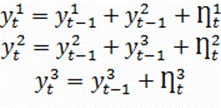
Компонента , компонента , и компонента . Все компоненты вектора  будут типа I(З), и существует две коинтегрирующие комбинации, имеющие порядок интеграции 2 (соответствует ) и 1 (соответствует ). Ранг матрицы П вновь равен числу линейно независимых коинтегрирующих