Анализ временных рядов. Модели временного ряда. Структура временного ряда. Альтернативные формулы для коэффициента автокорреляции

Формула для расчета коэффициента автокорреляции первого порядка:

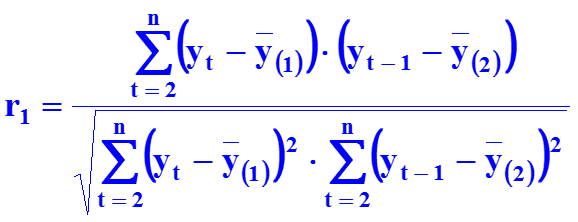
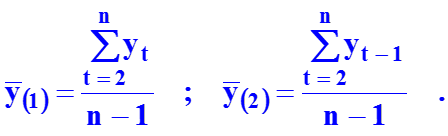
где

18

Коэффициент автокорреляции второго порядка

Аналогично можно определить коэффициенты второго (k=2) и более высоких порядков. Так, коэффициент авто-корреляции второго порядка характеризует тесноту связи между уровнями yt и yt-2 и определяется по формуле:

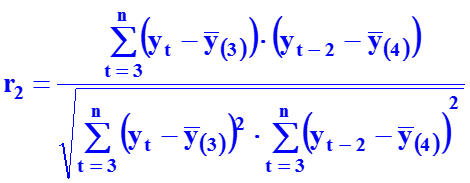
где

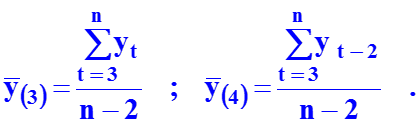
18

Альтернативные формулы для коэффициента автокорреляции

Альтернативная (приближенная) формула для расчета коэффициентов автокорреляции k-го порядка

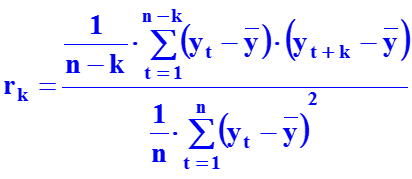
Пакет Statistica производит вычисления по формуле

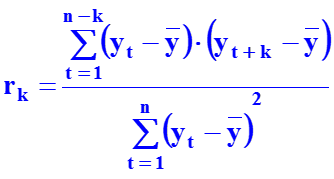
18

Частные коэффициенты автокорреляции

Частные коэффициенты автокорреляции более рельефно отражают структуру временного ряда. Они вычисляются при устранении влияния промежуточных уровней ряда. Например, частный коэффициент первого порядка (ему соответствует величина лага k=2) вычисляется по формуле:

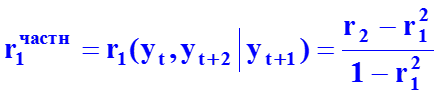
где r1 и r2 – исходные коэффициенты автокорреляции 1-го и 2-го порядка. Частные коэффициенты автокорреляции более высоких порядков могут быть подсчитаны по формулам, которые применялись ранее при вычислении частных коэффициентов корреляции.

18

Автокорреляционная функция

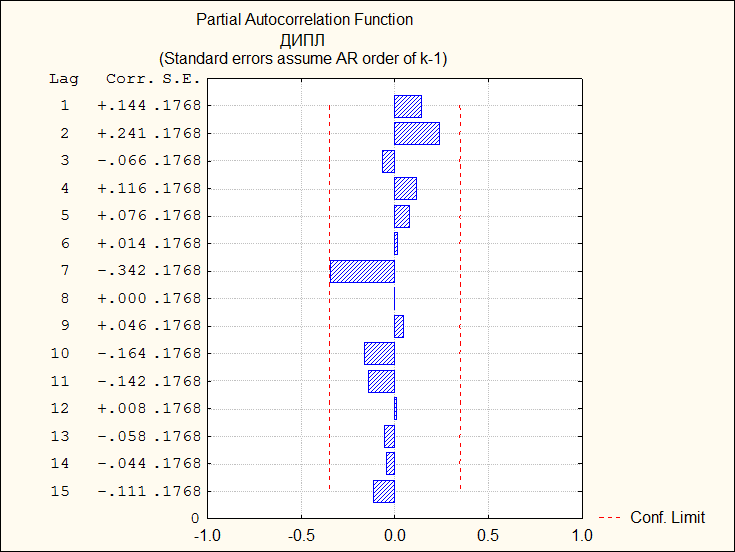
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага (порядка коэффициента автокорреляции) называют коррелограммой. Если наиболее высоким оказался коэффициент авто-корреляции первого порядка, то исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка , ряд содержит циклические колебания с периодичностью  моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, то ряд не содержит тенденции и циклических колебаний (содержит лишь случайную компоненту) либо ряд содержит сильную нелинейную тенденцию, которую следует учесть при выборе модели.

Пример временного ряда

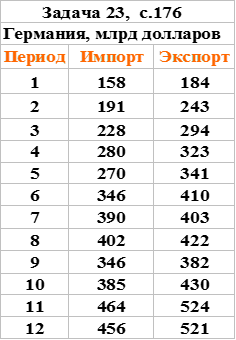
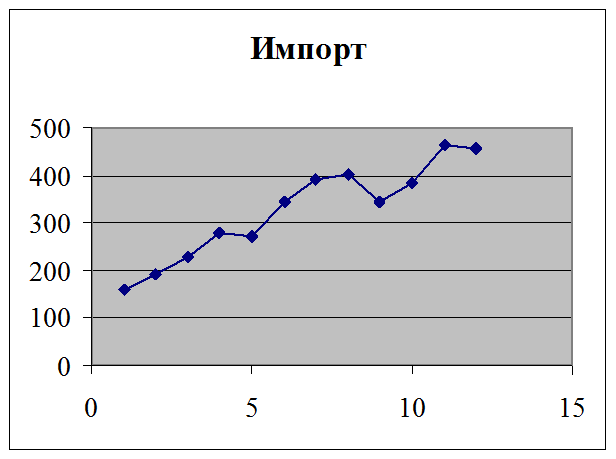
Построение коррелограммы временного ряда

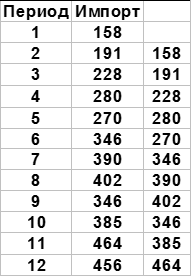
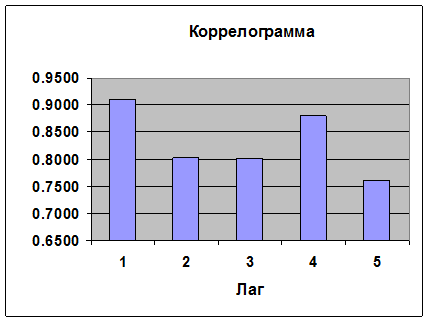
Коррелограмма при наличии тренда временного ряда

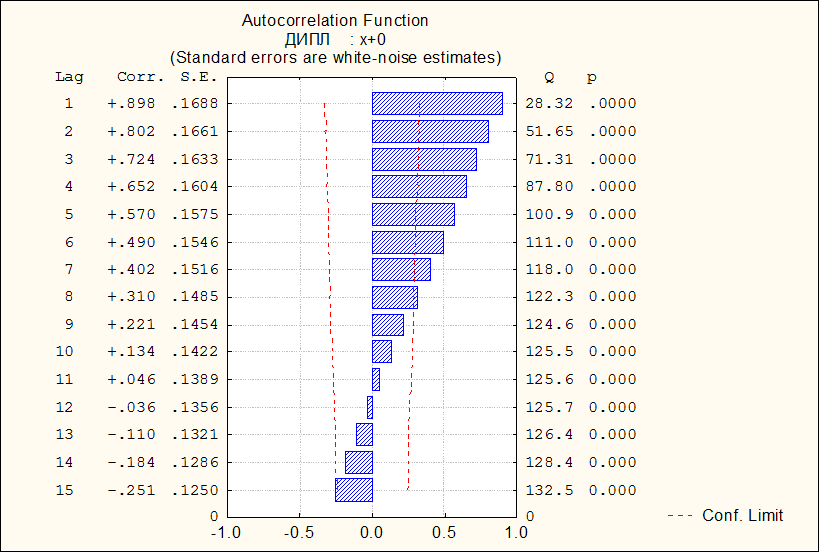
Частная автокорреляционная функция при наличии тренда временного ряда

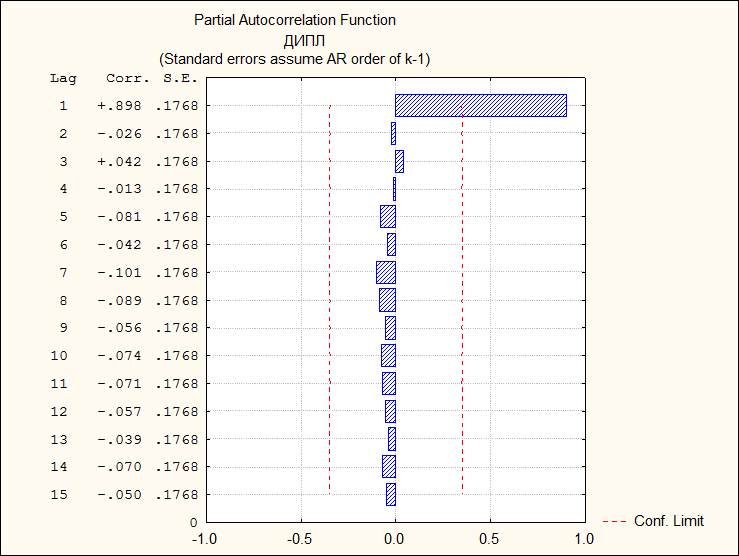
Автокорреляционная функция для стационарного случайного процесса

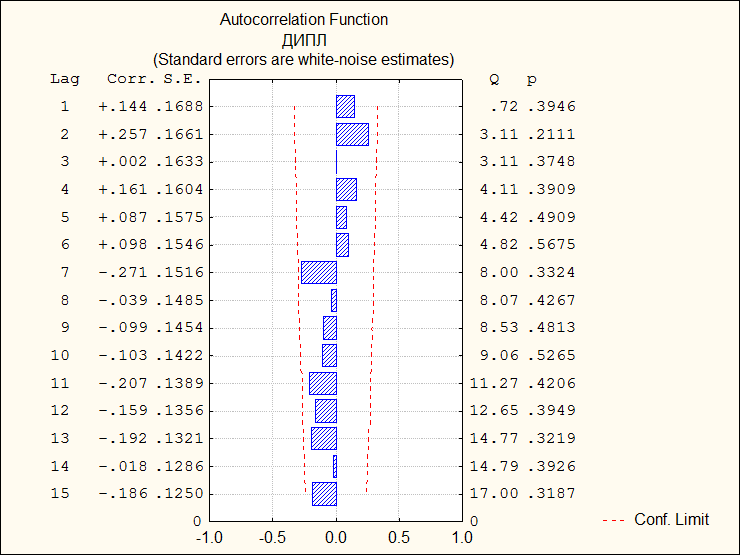
Частная автокорреляционная функция для стационарного случайного процесса

4.2. Моделирование временного ряда

Моделирование временного ряда состоит в построении аналитической или алгоритмически заданной функции, характеризующей зависимость уровней ряда от времени

19

Функции для описания тенденции (тренда) временного ряда

Построение аналитической функции для описания тенденции (тренда) временного ряда называют выравниванием (сглаживанием) временного ряда. Для этого применяются следующие функции: ·        линейная ·        логарифмическая ·        степенная ·        экспонента ·        парабола второго и более высоких порядков ·        гипербола Параметры трендов определяются обычным МНК, в качестве независимой переменной выступает время t = 1, 2, … , n, а в качестве зависимой переменной – фактические уровни ряда yt, t = 1, 2, … , n. Критерием отбора наилучшей формы тренда является наибольшее значение коэффициента детерминации R2, а при близких значениях R2 для разных моделей учитывается возможность наглядной экономиче-ской интерпретации параметров модели.

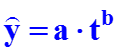
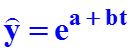
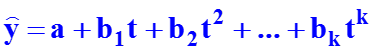
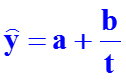
19

Функции тренда для тестового временного ряда

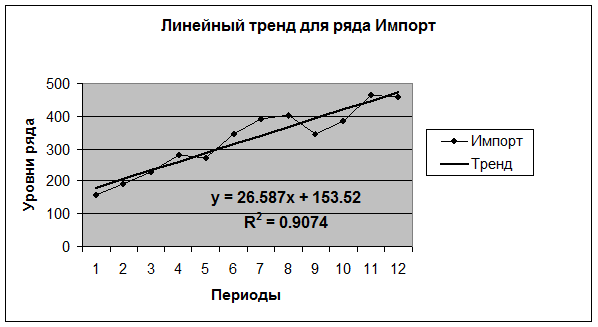
Моделирование структурных изменений

Структурные изменения в экономической системе, связанной с исследуемым временным рядом, могут вызвать резкое изменение характера тренда, начиная с момента t*, когда произошли эти структурные изменения.

yt

*

*

*

*

Общ.

*

*

*

*

1

*

*

*

*

*

*

*

*

*

*

*

*

2

t

t*

При структурных изменениях для аналитического описания тренда следует применить кусочно-линейную функцию, рассматривая раздельно два ряда с аргументами 1, ..., t* и t*+1, ..., n.

Тест Чоу

Целесообразность применения кусочно-линейной функции вместо общей (линейной) модели оценивается тестом Чоу. Проверяется гипотеза H0 о структурной стабильности тенденции изучаемого ряда на основе сравнения остаточных сумм квадратов для общей и кусочно-линейной моделей. Остаточную сумму квадратов по кусочно-линейной модели находят как   где - остаточная сумма квадратов по кусочно-линейной модели; - остаточная сумма квадратов для ряда y1, y2, ... , yt*;  - остаточная сумма квадратов для ряда yt*+1,... , yn.   Число степеней свободы, соответствующее , равно (n1 - k1) + (n2 - k2) = n - k1 - k2 где k1 и k2 - число параметров в 1-й и 2-й моделях соответственно.

21

Применение F-критерия в тесте Чоу

Сокращение остаточной суммы квадратов отклонений при переходе