Многомерные процессы. Эндогенные и экзогенные переменные. Вектор математических ожиданий

Идея доказательства заключается в стандартном сведении системы разностных уравнений порядка р для n переменных к системе разностных уравнений первого порядка, но для pn переменных. Матрица преобразованной системы обладает блочной структурой, а характеристические уравнения исходной и преобразованной систем совпадают. Эта часть доказательства и является наиболее сложной технически. Для исходного уравнения, как мы уже упоминали, характеристическое уравнение имеет вид: . Следовательно, существование единичного корня у исходного уравнения эквивалентно существованию нулевого корня у вышеприведенной матрицы П. С помощью рассуждений, аналогичных проведенным выше, мы приходим к следующему заключению. Ранг матрицы  равен числу линейно независимых коинтегрирующих векторов. Этот показатель принято называть коинтегрирующим рангом.

Итак, если между компонентами вектора  существуют коинтегрирующие соотношения, то их количество равно количеству нулевых собственных чисел матрицы П, причем не все коинтегрирующие соотнощения дают стационарные линейные комбинации.

Лекций 15

Коинтеграционная регрессия и тестирование коинтеграции

До сих пор мы рассматривали коинтеграцию как некоторое сугубо теоретическое свойство. Посмотрим, что меняет наличие этого свойства для оценивания регрессий с нестационарными переменными. Вернемся к рассмотренному в предыдущей лекции примеру Грэнжера и Энгла: случайные процессы  и  определены следующими соотношениями ,  где , и  ( и  — некоррелированные белые щумы). Мы уже установили, что  и  коинтегрированы. Пусть у нас есть выборка объема Т из обеих переменных. Попробуем построить обычную регрессию  на методом наименьших квадратов. Как мы помним, в этом случае существует опасность получить в результате кажущуюся регрессию. Удивительная вещь заключается в следующем. Несмотря на то, что  и  являются процессами типа I(1) , оказывается, что в случае, если процессы коинтегрированы, оценка МНК коэффициентов регрессии становится состоятельной. И можно, несмотря на нестационарность переменных, применять обычные регрессионные методы.

Давайте посмотрим, почему это так. Оценка коэффициента наклона в регрессии  будет выражена известным выражением 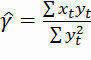. Поскольку математические ожидания обеих переменных равны нулю, можно заменить в этом выражении строчные буквы прописными. Используем приведенную форму нашей системы:

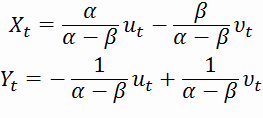
Используя теорему Слуцкого и тот факт, что дисперсия стационарного процесса постоянна, а дисперсия процесса  случайного блуждания и, стремится к  бесконечности, получим:

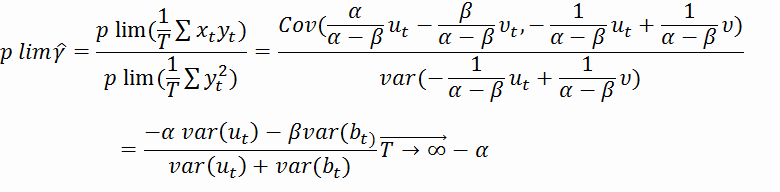
Следовательно, оценка МНК коэффициента наклона является состоятельной оценкой нормированного коинтегрирующего соотношения. Более того, можно показать, что скорость сходимости оценки выше, чем в случае оценки МНК для стационарных регрессий. Поскольку дисперсия случайного блуждания растет пропорционально Т , скорость сходимости при наличии коинтеграции пропорциональна  в то время как для стационарных регрессоров скорость сходимости пропорциональна только это свойство оценок МНК при наличии коинтеграции называют суперсостоятелъностъю.

Однако регрессия  на  использует не всю информацию, содержащуюся в исходной модели. Умножим второе из уравнений приведенной формы на α и сложим с первым уравнением. Получим . Стандартным образом получаем:

или

Полученное выражение представляет собой уже знакомую нам модель коррекции ошибками, в котором коинтегрирующее соотношение играет роль долгосрочного соотношения между переменными. Эта модель соответствует модели ADL(1,1) с нестационарными регрессорами, а именно: . Понятно, что ЕСМ и ADL(1,1) являются различными параметризациями одной и той же модели. При этом, если оценивать модель в виде ЕСМ методом наименьших квадратов, то как объясняемая переменная , так и регрессоры  и  являются стационарными. Поэтому оценки коэффициентов ЕСМ-представления заведомо состоятельны. Поскольку оценки ADL-представления однозначно пересчитываются через оценки ЕСМ-представления, они также состоятельны.

Общий результат, полученный Симсом, Стоком и Уотсоном, состоит