Построение графика временных рядов средней цены заданных книг и курса доллара (евро) за заданный период

Начальное сглаженное значение принимается равным начальному значению временного ряда.

Сглаженные значения, полученные с использованием пакетов "Анализ данных" и STATISTICA, совпадают.

Адаптивный метод Брауна

a₀(t) = a₀(t – 1) + a₁(t – 1) + e(t) * (1 – l²),

a₁(t) = a₁(t – 1) + e(t) * (1 – l)²

Оценка начальных параметров модели МНК по первым пяти точкам:

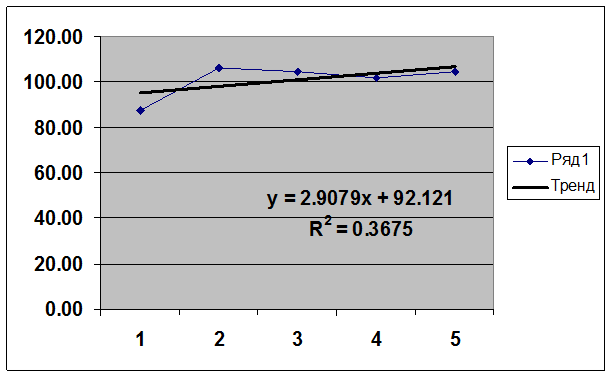
а₁(0)=  2.9079

а₀(0)=  92.121

k = 1    - количество шагов прогнозирования;

l = 0.3 - коэффициент дисконтирования данных.

t	Факт	a0(t)	a1(t)	Расчет	Отклонение
	Y(t)			Yр(t)	e(t)
0	-	92.121	2.9079	-	-
1	87.59	88.26	-0.74	95.03	-7.44
2	106.05	104.38	8.34	87.53	18.52
3	104.64	105.37	4.38	112.72	-8.08
4	101.57	102.31	0.37	109.75	-8.18
5	104.37	104.22	1.20	102.68	1.69
6	93.63	94.69	-4.58	105.42	-11.79
7	106.62	105.14	3.51	90.11	16.51
8	104.78	105.13	1.62	108.65	-3.87
9	111.37	110.95	3.88	106.74	4.62
10	118.80	118.44	5.82	114.83	3.96
11	107.55	109.05	-2.37	124.27	-16.72
12	117.70	116.71	3.03	106.68	11.02
13	112.74	113.37	-0.40	119.74	-7.00
14	100.45	101.58	-6.54	112.98	-12.53
15	111.52	110.04	1.54	95.04	16.48
16	123.91	122.80	7.58	111.57	12.33
17	109.79	111.64	-2.51	130.38	-20.59
18	129.29	127.47	7.37	109.13	20.16
19	109.98	112.22	-4.81	134.84	-24.86
20	111.40	111.04	-2.86	107.40	3.99
21	116.01	115.30	0.98	108.18	7.83
22	113.56	113.80	-0.36	116.28	-2.73
23	121.19	120.50	3.44	113.45	7.75
24	117.71	118.27	0.39	123.94	-6.22
25	116.28	116.49	-0.78	118.66	-2.38
26	117.29	117.15	-0.01	115.72	1.58
27	110.57	111.16	-3.23	117.14	-6.58
28	119.87	118.80	2.62	107.93	11.94
29	144.94	142.82	14.15	121.42	23.52
30	129.97	132.40	0.92	156.97	-27.00
31	124.15	124.98	-3.57	133.32	-9.17
32	132.12	131.16	1.68	121.40	10.72

При прогнозировании используется модель, построенная на последнем шаге:

y(32+k) = 131.16 + 1.68*k

Анализ остатков и прогноз

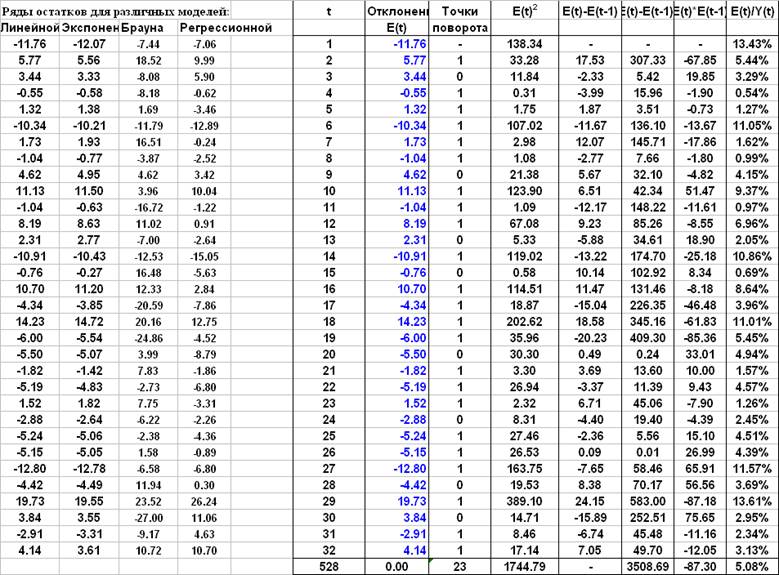
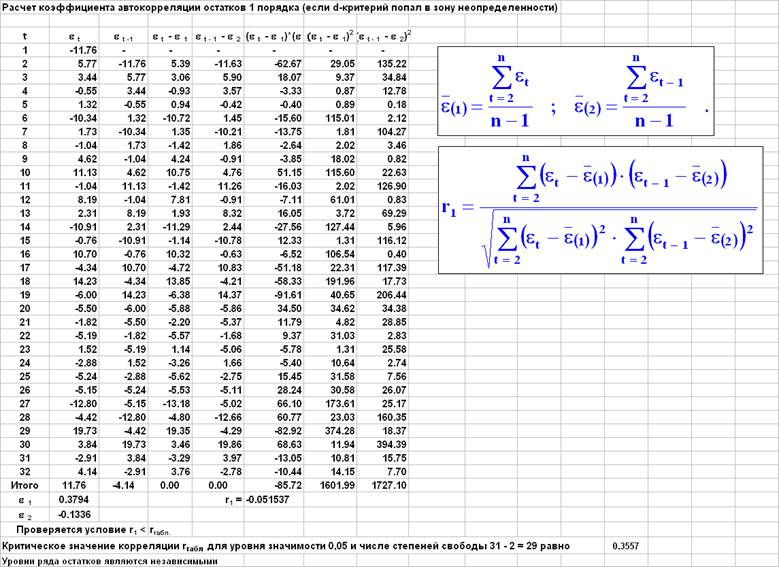
Тесты Колмогорова-Смирнова для проверки гипотезы о нормальном распределении остатков.

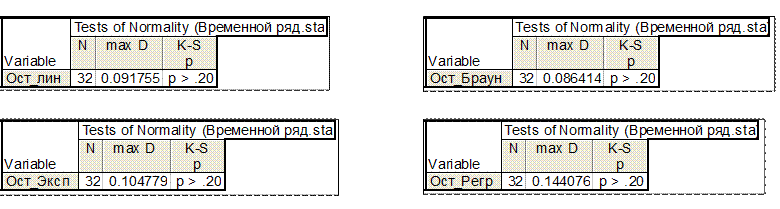
Результаты анализа остатков для различных моделей:

Для линейной, экспоненциальной и регрессионной моделей соблюдаются предпосылки МНК, однако, вследствие низкой величины коэффициентов детерминации они могут использоваться  лишь для предварительного прогноза анализируемого показателя.

Прогноз по линейной модели

          

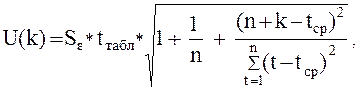
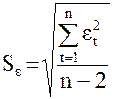
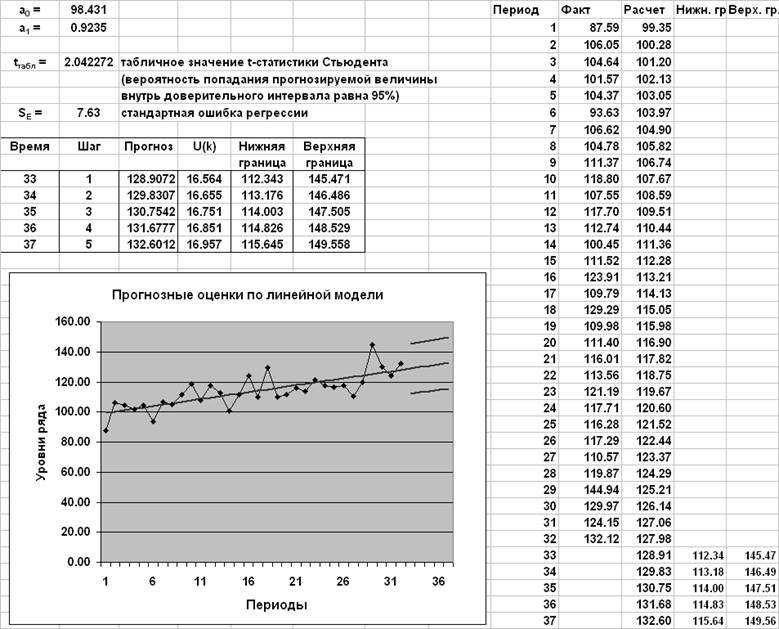
Прогноз по экспоненциальной модели

Прогноз строится для линеаризованной модели (для Ln(y)), затем пересчитывается на исходные значения y.

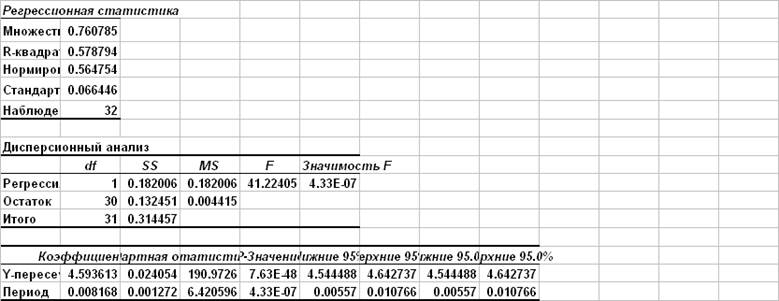
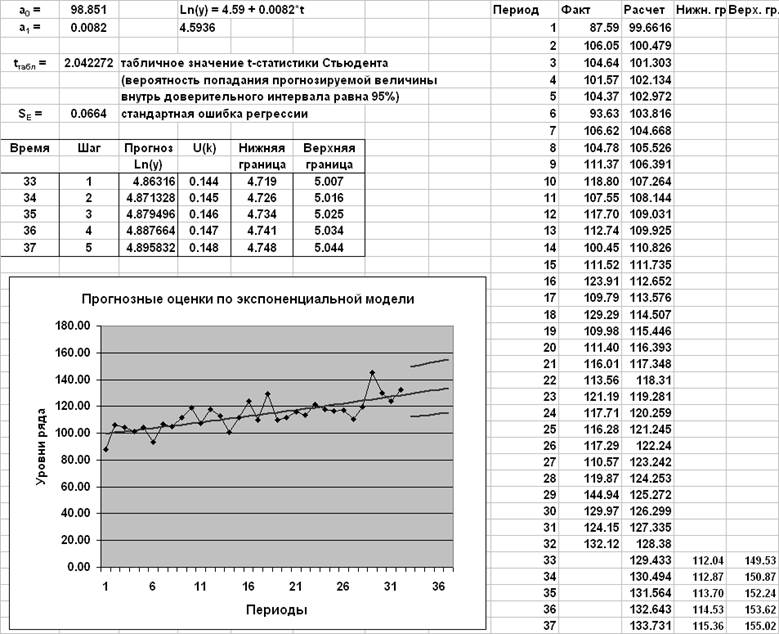
Прогноз по модели Брауна

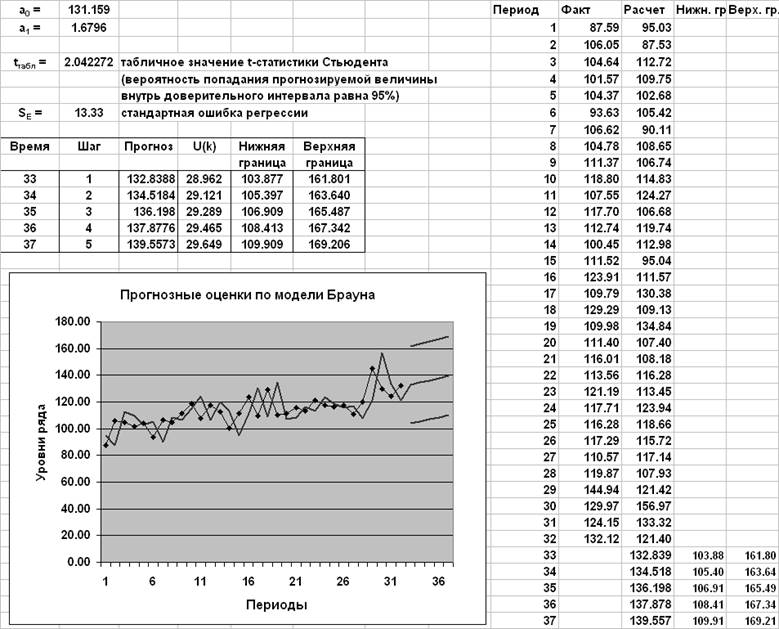
Прогноз по регрессионной модели

Сначала рассчитываются прогнозные значения курса Евро (по степенному тренду):

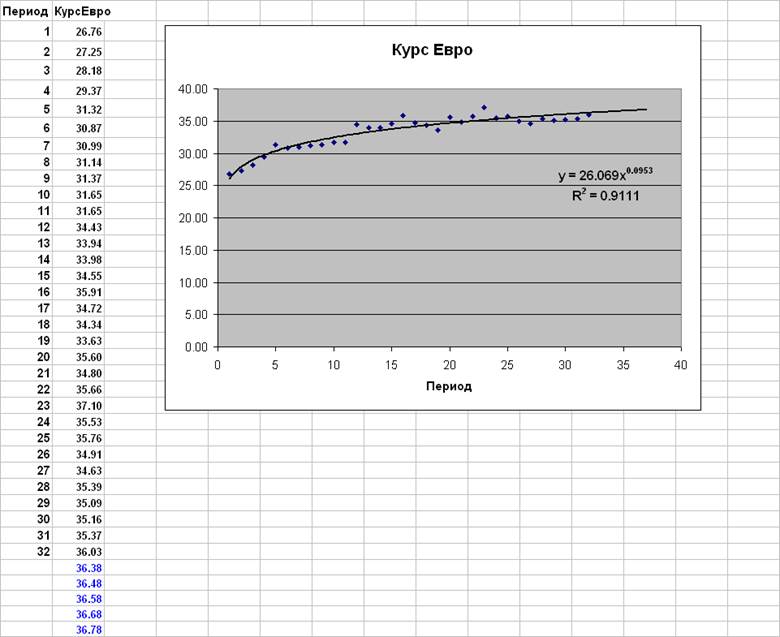
Далее прогнозные значения курса Евро используются для расчета точечного прогноза средних цен книг по разделу Компьютерная литература.

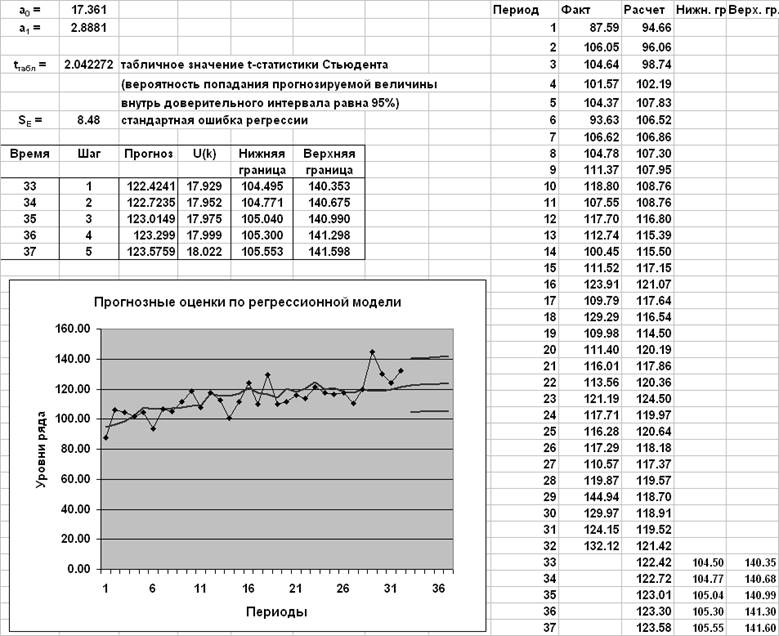
Модели ARIMA

Спецификация моделей ARIMA

Графики и коррелограммы первых и вторых разностей временного ряда Компьютерная литература

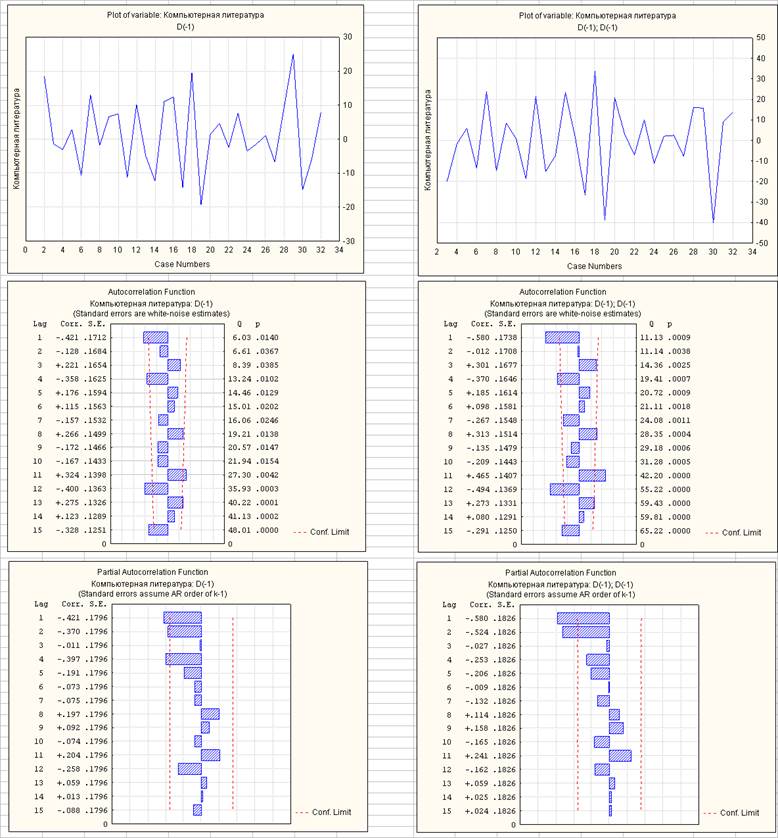
Автокорреляционные и частные автокорреляционные функции первых и вторых разностей рассматриваемого временного ряда имеют некоторое сходство с коррелограммами, полученными при моделировании процесса AR(1) с отрицательным значением коэффициента f₁ и процесса ARMA(1, 1) с отрицательными значениями коэффициентов f₁ и q₁:

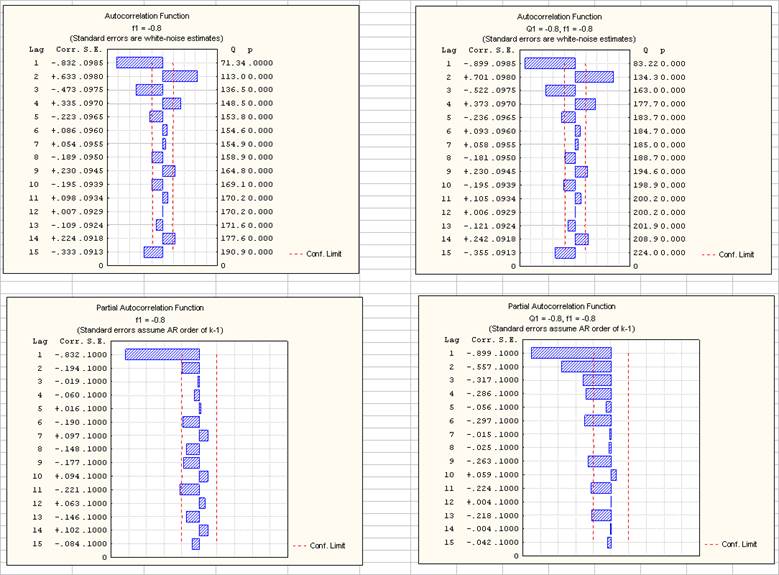
В связи с этим наряду с другими моделями целесообразно рассмотреть модели ARIMA(0 1, 1),  ARIMA(0, 2, 1), ARIMA(1, 1, 1), ARIMA(1, 2, 1).

Построение наиболее популярных моделей ARIMA

p=0, d=1, q=1

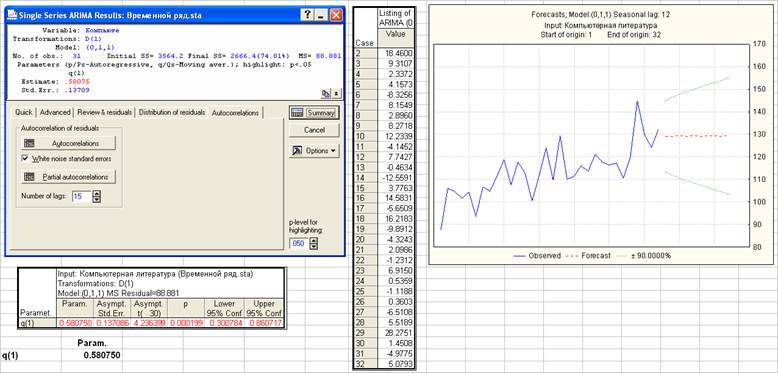
Расчеты по формулам:

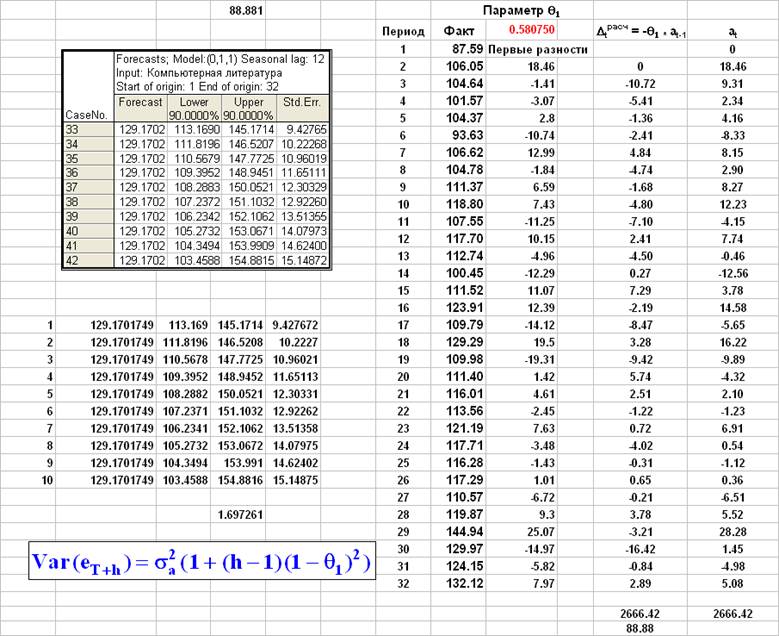
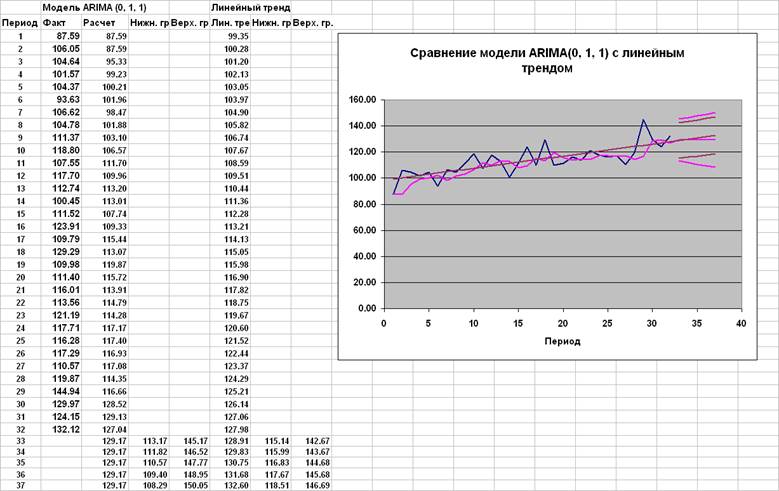
Модель ARIMA(0, 1, 1) не содержит незначимых параметров. Стандартная ошибка прогноза на 1 шаг для модели ARIMA(0, 1, 1) равна 9.43 против 8.11 (с. 20) для линейной модели.

p=0, d=2, q=2

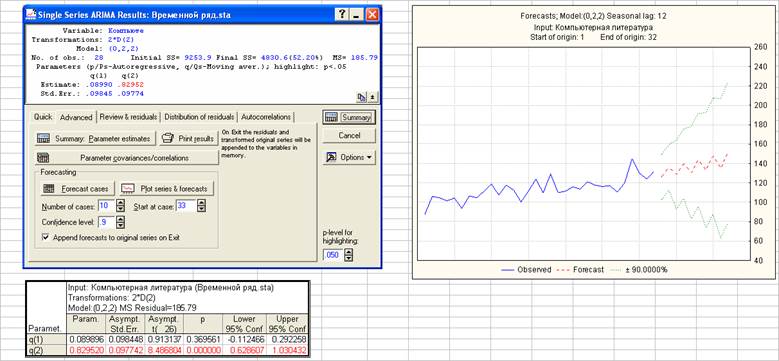
Модель ARIMA(0, 2, 2) содержит незначимый параметр q(1), поэтому далее не рассматривается.

p=1, d=1, q=1

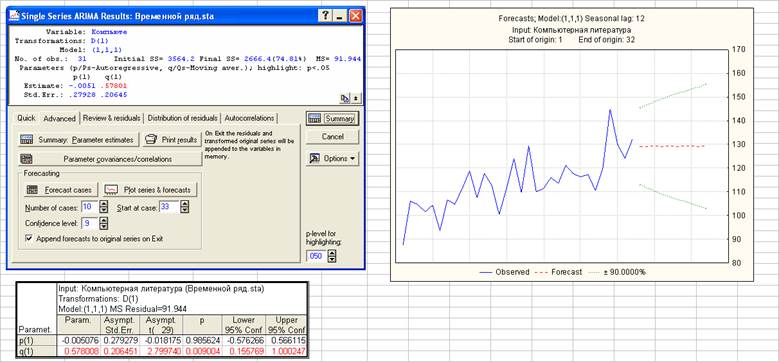
Модель ARIMA(1, 1, 1) содержит незначимый параметр p(1), поэтому далее не рассматривается.

p=1, d=1, q=0

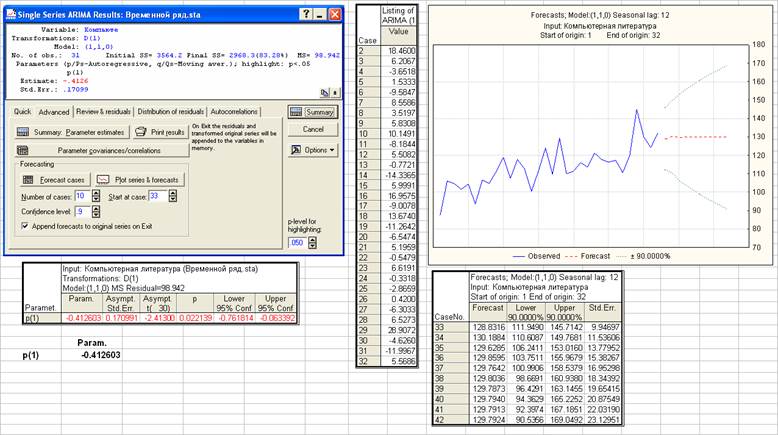
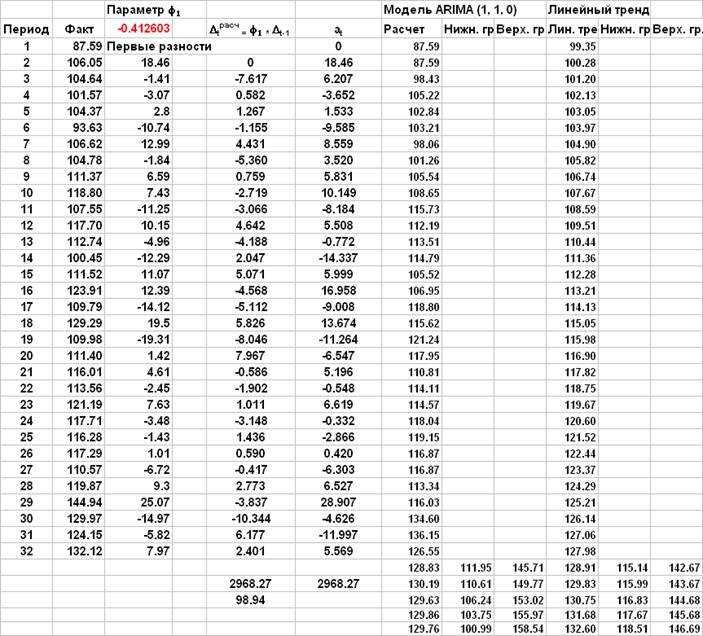
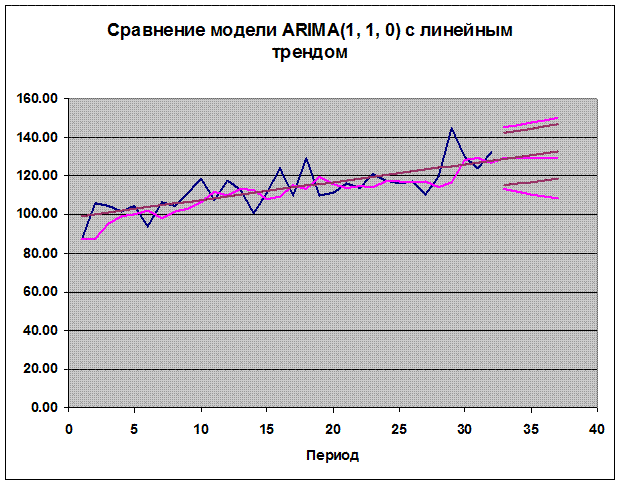
Модель ARIMA(1, 1, 0) не содержит незначимых параметров. По точности прогноза  модель ARIMA (1, 1, 0) несколько уступает модели ARIMA (0, 1, 1). Стандартная ошибка прогноза на 1 шаг равна 9.94 против 9.43 для модели ARIMA (0, 1, 1).

p=2, d=1, q=0

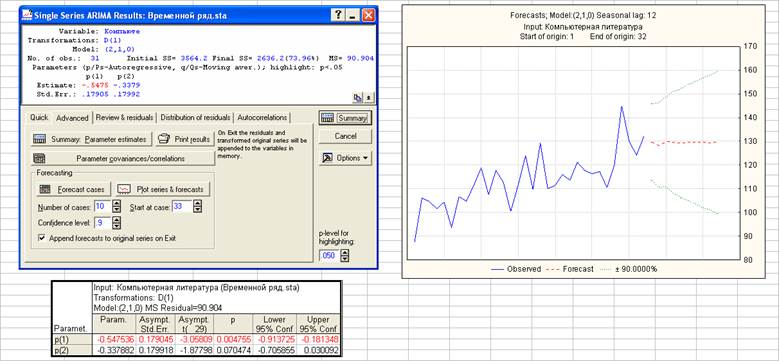
Модель ARIMA(2, 1, 0)  содержит незначимый параметр p(2), поэтому далее не рассматривается.

p=2, d=2, q=0

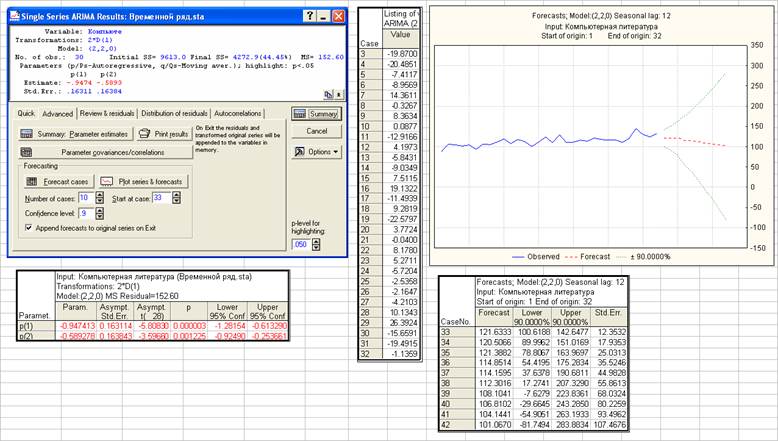
По точности прогноза модель ARIMA (2, 2, 0) уступает модели ARIMA (0, 1, 1). Стандартная ошибка прогноза на 1 шаг равна 12.35 против 9.43 для модели ARIMA (0, 1, 1).

Построение дополнительных моделей ARIMA

Построенные ранее автокоррелограмма и частная автокоррелограмма для исходного временного ряда с некоторым приближением соответствуют модели авторегрессии 1-го порядка:

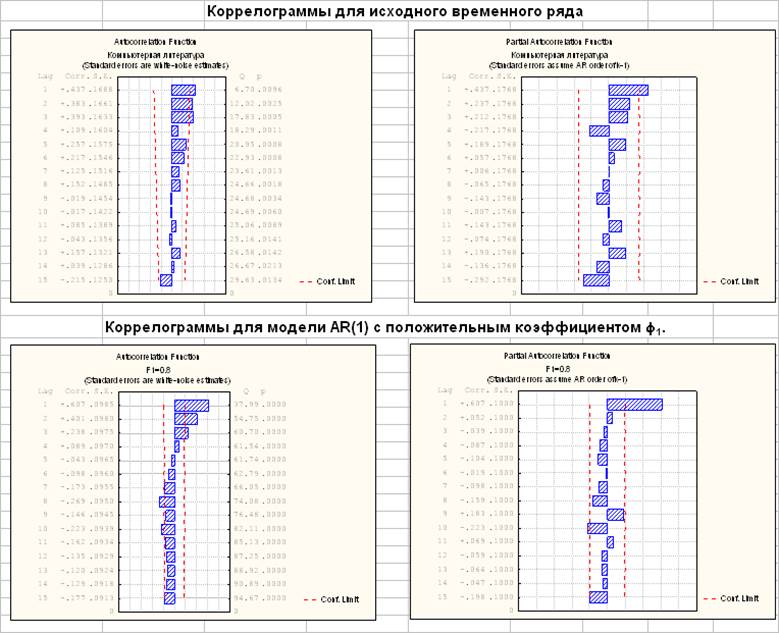
Поэтому наряду с заданными шестью моделями целесообразно оценить модель (1, 0,.0).

p=1, d=0, q=0

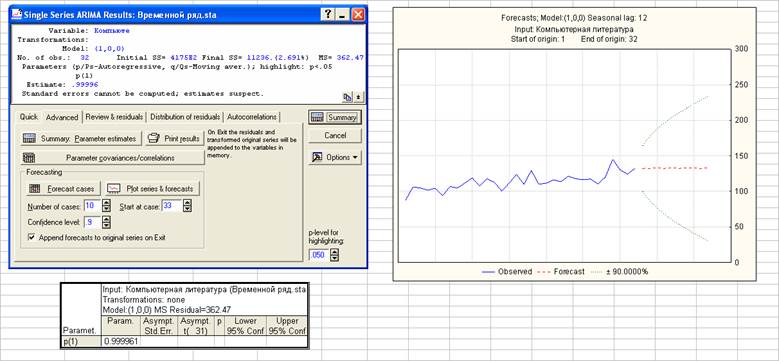
Модель ARIMA (1, 0, 0) соответствует нестационарному случайному процессу (процессу случайного блуждания), поэтому далее не рассматривается.

Автокоррелограмма и частная автокоррелограмма для вторых разностей с некоторым приближением соответствуют модели авторегрессии 1-го порядка с отрицательным коэффициентом f₁:

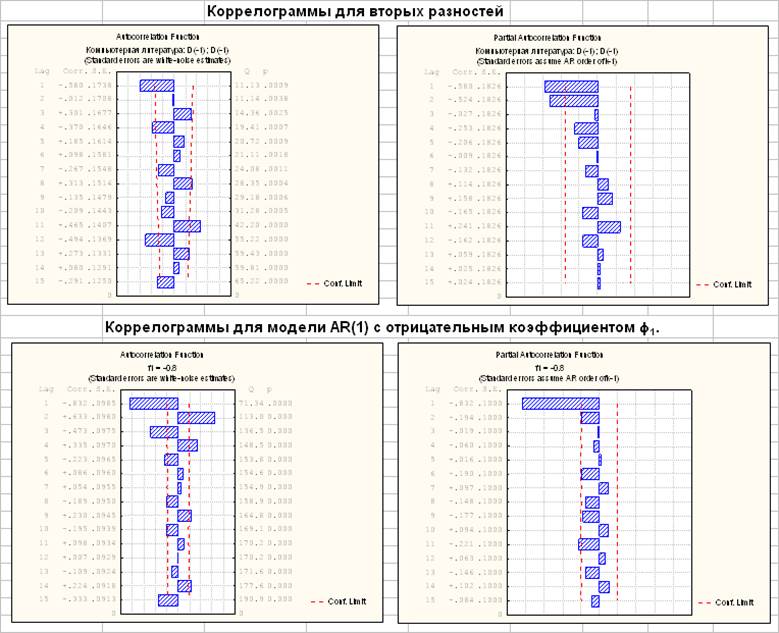
Поэтому дополнительно рассматривается модель ARIMA (1, 2, 0).

\p=1, d=2, q=0

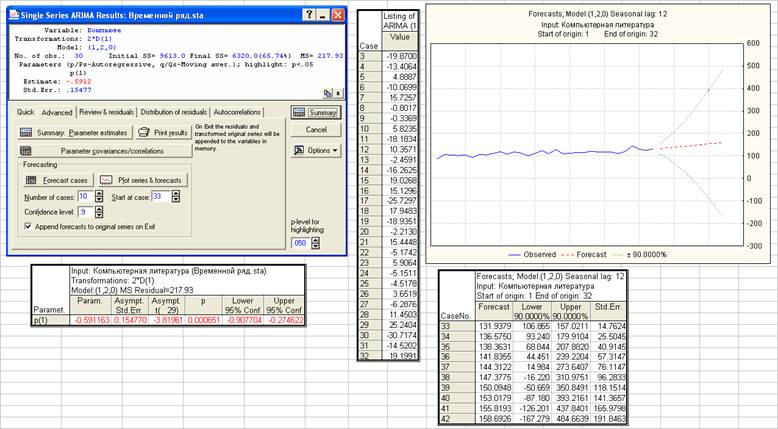
По точности прогноза модель ARIMA (1, 2, 0) значительно уступает модели ARIMA (0, 1, 1). Стандартная ошибка прогноза на 1 шаг равна 14.76 против 9.43 для модели ARIMA (0, 1, 1).

Модель для регрессионных остатков линейного тренда (комбинированная модель)

Для регрессионных остатков линейного тренда путем перебора различных моделей ARIMA выбрана модель ARIMA (0, 1, 1), в которой отсутствуют незначимые параметры и которой по сравнению с другими оцененными моделями без незначимых параметров соответствует минимальная величина стандартной ошибки прогноза для 1-го шага.

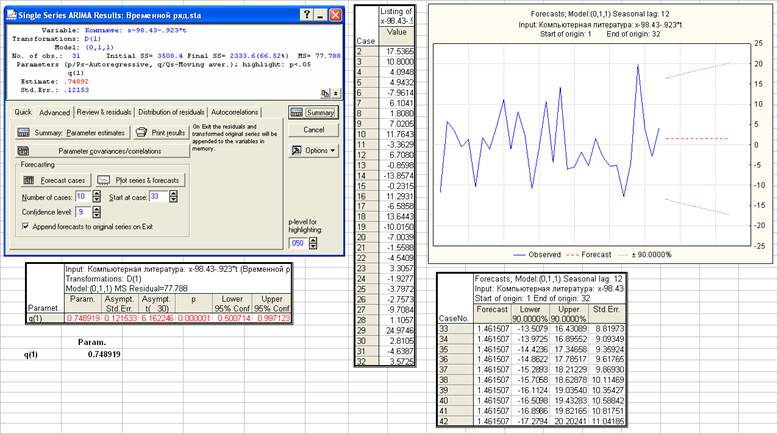
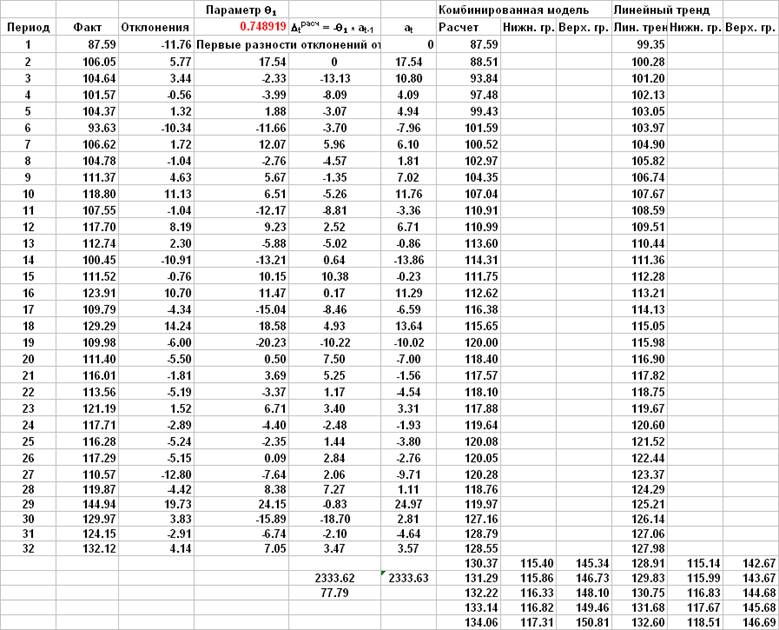
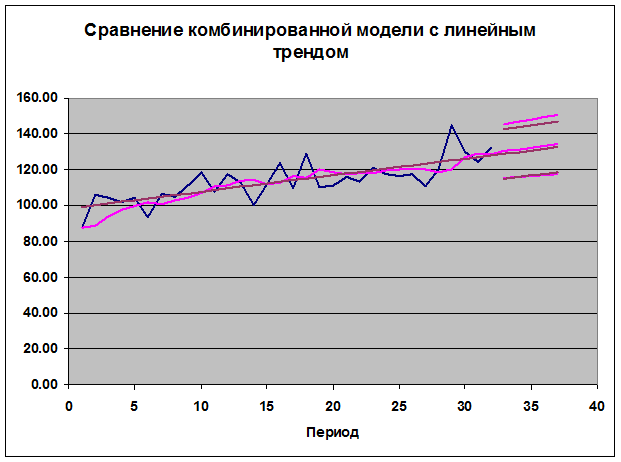
По точности прогноза комбинированная модель несколько превосходит модель ARIMA (0, 1, 1). Стандартная ошибка прогноза на 1 шаг равна 8.82 против 9.43 для модели ARIMA (0, 1, 1).

Вывод:

Из 8 рассмотренных моделей ARIMA лучшими являются модели ARIMA (0, 1, 1) и   ARIMA (1, 1, 0).  Они не содержат незначимых параметров, им соответствуют наименьшие по сравнению с другими рассмотренными моделями значения стандартной ошибки прогноза 1-го шага: 9.43 и 9.94 (соответствующая величина для линейного тренда равна 8.11). Наряду с моделями ARIMA рассмотрена комбинированная модель, сочетающая линейный тренд с моделью ARIMA (0, 1, 1) для отклонений от тренда. Стандартная ошибка прогноза на 1 шаг для комбинированной модели