Определите средний уровень специального звания таможенных работников.
Глава 5. Показатели вариации и анализ частотных распределений
5.1. Показатели вариации
5.2. Ряды распределения
5.3. Показатели формы распределения
5.4. Теоретическое распределение в анализе вариационных рядов. Критерии согласия
Гусаров В.М. Теория статистики. М.: Аудит, ЮНИТИ, 1998.
Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. М.: ИНФРА-М, 1996.
Статистика: Курс лекций/ Под ред. .- Новосибирск: Изд-во НГАЭиУ, 1996.
Шмойлова Р.А. Теория статистики. М.: Финансы и статистика, 1996.
Практикум по теории статистики: Учебное пособие/ Под ред. проф. . - М.: Финансы и статистика, 1998.
Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник/Под ред. О.Э.Башиной, А.А. Спирина. – 5-е изд., доп. и перераб.- М.: Финансы и статистика,1999.
5.1.

|
 |

Абсолютные

|
 |
|||
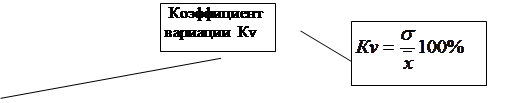 |
|||

|
![]()
|
 |
|||
Расчет показателей вариации по стажу работников двух бригад
|
I |
бригада |
II |
бригада |
|||
|
№ п.п. |
Стаж, год х |
Отклонение от среднего стажа
|
Квадрат отклонения от среднего стажа
|
Стаж, год |
Отклонение от среднего стажа
|
Квадрат отклонения от среднего стажа
|
|
1 |
1 |
6,2 |
38,44 |
6 |
1,2 |
1,44 |
|
2 |
2 |
5,2 |
27,04 |
6 |
1,2 |
1,44 |
|
3 |
3 |
4,2 |
17,64 |
7 |
0,2 |
0,04 |
|
4 |
3 |
4,2 |
17,64 |
7 |
0,2 |
0,04 |
|
5 |
4 |
3,2 |
10,24 |
7 |
0,2 |
0,04 |
|
6 |
9 |
1,8 |
3,24 |
7 |
0,2 |
0,04 |
|
7 |
10 |
2,8 |
7,84 |
8 |
0,8 |
0,64 |
|
8 |
12 |
4,8 |
23,04 |
8 |
0,8 |
0,64 |
|
9 |
13 |
5,8 |
33,64 |
8 |
0,8 |
0,64 |
|
10 |
15 |
7,8 |
60,84 |
8 |
0,8 |
0,64 |
|
Сумма |
72 |
46 |
239,6 |
72 |
6,4 |
5,6 |
Последовательность расчета:
1. Рассчитываем средний стаж работы
работников в каждой бригаде в годах: в первой бригаде - 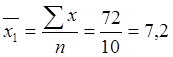
во второй
бригаде - 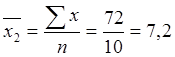
2. Определяем размах вариации:
в первой бригаде - R1 = Хmax – Xmin = 15-1=14 лет во второй бригаде – R2 = Хmax – Xmin = 8-6 = 2 года
Это свидетельствует о том, что при численном равенстве работников бригад колеблемость стажа отдельных работников во второй бригаде значительно меньше, чем в первой.
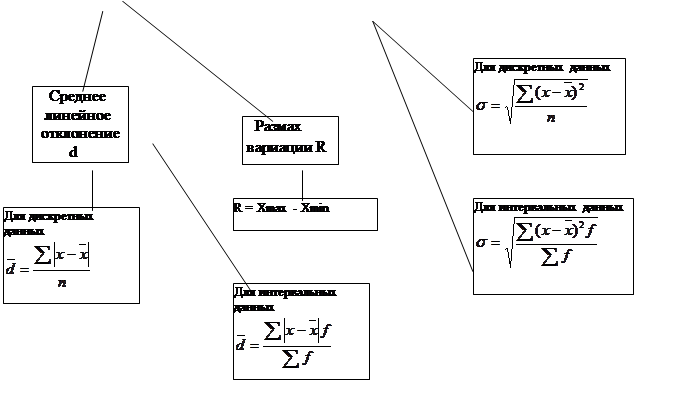
3. Вычисляем среднее линейное отклонение:
в первой бригаде - 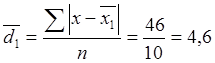 года во второй бригаде -
года во второй бригаде - 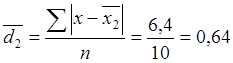 года
года
Во второй бригаде стаж работников более однороден, чем в первой бригаде.
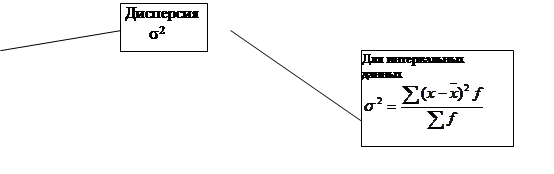
4. Дисперсия для первой бригады составит:
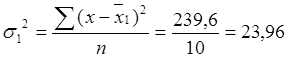 года для второй бригады -
года для второй бригады - 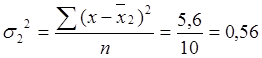 года
года
5. Среднее квадратическое отклонение:
в первой бригады - ![]() года во второй бригады -
года во второй бригады - ![]() года
года
Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность. Во второй бригаде дисперсия и среднее квадратическое отклонение значительно меньше, чем в первой бригаде, следовательно, средняя арифметическая второй бригады является обобщающей характеристикой всей совокупности.
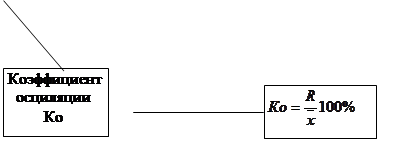
6. Коэффициент осциляции в первой бригаде составил:
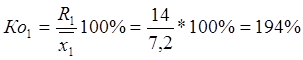 , т.е. разница между крайними значениями на 94% превышает среднее
значение стажа работников.
, т.е. разница между крайними значениями на 94% превышает среднее
значение стажа работников.
В то же время во второй бригаде этот
показатель составляет 27,2 % среднего значения: 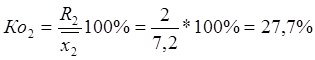 .
.
7. Относительное линейное отклонение
характеризует долю усредненного значения абсолютных отклонений от средней
величины, и во второй бригаде оно составило 8,8% против 64% в первой бригаде: 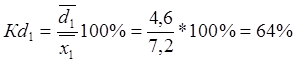 ,
, 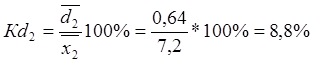
8. Коэффициент вариации используется для оценки типичности средних величин и равен:
в первой бригаде - 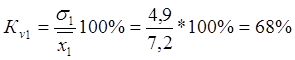
во второй бригаде - 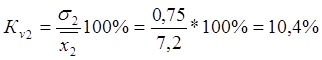
Чем меньше значения относительных показателей вариации, тем меньше колеблемость признаков, что подтверждает однородность совокупности. Если Кv 40%, то это говорит о большой колеблемости признака и не типичности средней величины для всей совокупности. В нашем примере коэффициент вариации подтверждает большую колеблемость стажа работников в первой бригаде и, следовательно, средняя арифметическая не является обобщающей характеристикой всей совокупности.
5.2. Ряды распределения.
![]()
![]()
Атрибутивные Дискретные
( качественные) ( прерывные)
![]()
![]()
Вариационные Интервальные
![]() (количественные) ( непрерывные)
(количественные) ( непрерывные)
![]()
![]() с равными с неравными интервалами интервалами
с равными с неравными интервалами интервалами
5.3. Показатели формы распределения.
5.4. Теоретические распределения в анализе вариационных рядов. Критерии согласия.
![]()
Нормальное
![]()
![]() распределение
распределение
Распределение Биноминальное
![]() Максвелла распределение
Максвелла распределение
Гамма Распределение распределение Пуассона
|
1.Что характеризует коэффициент асимметрии ?
2.По данным о распределении количества обрабатываемых за неделю ГТД, рассчитайте показатель асимметрии и эксцесса:
|
Кол-во обрабатываемых в неделю ГТД, шт |
19 - 20 |
20 - 21 |
21 - 22 |
22 - 23 |
23 - 24 |
24 - 25 |
Итого: |
|
частота |
2 |
22 |
155 |
251 |
67 |
5 |
502 |
3.Что представляют собой ряды распределения?
4.Какие системы показателей используют для характеристики особенностей рядов распределения?
5.Каковы особенности кривых нормального распределения?
6.В чем состоит значение проверки гипотезы о форме нормального распределения?
7.По следующим данным постройте интервальный ряд распределения.
Возраст студентов двух групп 5 курса, лет :
22 21 23 24 22 21 22 21 23 26 24 21
25 23 22 21 21 22 24 23 21 21 25 24
8.Пользуясь критерием согласия Пирсона установите, согласуются ли данные о распределении мужчин по росту с предположением о распределении их по нормальному закону.
|
Наблюдаемые частоты |
11 |
26 |
65 |
120 |
181 |
201 |
170 |
120 |
64 |
28 |
14 |
Итого: 1000 |
|
Теоретические частоты |
11 |
27 |
65 |
120 |
175 |
198 |
175 |
122 |
66 |
28 |
11 |
998 |
Глава 6. Выборочный метод в статистике
6.1. Выборочное наблюдение, его задачи
6.2. Ошибки выборки
Гусаров В.М. Теория статистики. М.: Аудит, ЮНИТИ, 1998.
Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. М.: ИНФРА-М, 1996.
Статистика: Курс лекций/ Под ред. .- Новосибирск: Изд-во НГАЭиУ, 1996.
Шмойлова Р.А. Теория статистики. М.: Финансы и статистика, 1996.
Практикум по теории статистики: Учебное пособие/ Под ред. проф. . - М.: Финансы и статистика, 1998.
Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник/Под ред. О.Э.Башиной, А.А. Спирина. – 5-е изд., доп. и перераб.- М.: Финансы и статистика,1999.
6.1. Выборочное наблюдение, его виды.
6.2. Общая величина ошибки выборочной совокупности.
![]() Простая случайная
Простая случайная
выборка
![]()
![]()
![]()
Средняя ошибка Предельная ошибка для средней для средней
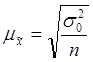
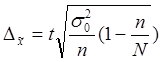
для доли для доли
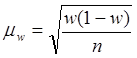
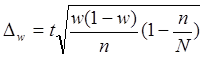
![]()
для средней для средней
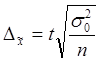
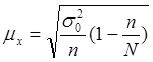
для доли для доли
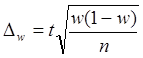
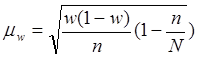
![]()
Пределыгенеральной средней
![]()
Пределы генеральной доли
![]()
s02 - дисперсия признака х в выборочной совокупности
w - доля единиц, обладающих исследуемым признаком
n - объем выборочной совокупности
N - объем генеральной совокупности
![]() -
выборочная средняя
-
выборочная средняя
![]() -
генеральная средняя
-
генеральная средняя
t - коэффициент доверия, который определяется в зависимости от того, с какой вероятностью надо гарантировать результаты выборочного наблюдения.
Коэф. доверияt 1,0 2,0 3,0
Вероятность Ф(t) 0,683 0,954 0,997
Пример.
В случае случайного повторного отбора было установлено, что средний вес товара в выборочной совокупности, состоящей из 100 изделий оказался равным 10 кг, при среднем квадратическом отклонении 0,6кг. С вероятностью равной 0,954 определить в каких пределах заключен средний вес товара в генеральной совокупности.
По условию задачи
имеем: ![]() =
10кг, n = 100 , s0 =0,6кг
=
10кг, n = 100 , s0 =0,6кг
Ф(t) = 0,954 ,следовательно t = 2.
Последовательность расчета:
1. Определяем среднюю и предельную ошибки выборки
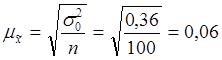 кг
кг
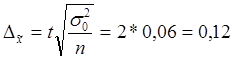 кг
кг
2. Средний вес
изделия в генеральной совокупности колеблется в пределах ![]()
![]()
![]()
Таким образом, с вероятностью 0, 954 можно утверждать, что средний вес товара в генеральной совокупности колеблется в пределах от 9,88 до 10,12 кг.
Механическая выборка
![]()
Генеральная совокупность с определенной последовательностью единиц
(в алфавитном порядке, по географической направленности и т.д.)
![]()
![]()
Отбор заданного числа единиц через определенный интервал при 2% выборке отбирается и проверяется каждая 50 единица (1/0,02)
при 5% выборке – каждая 20 единица (1/0,05)
![]()
![]()
по формулам случайного бесповторного отбора
Пример.
Из 1000 таможенных работников в порядке механической выборки отобрано
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.