8. Виды дисперсий и правило их сложения
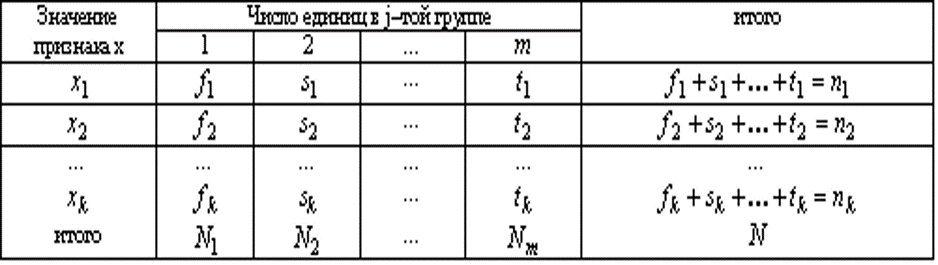
Рассчитаем m штук частных средних, т.е. среднее значение признака в каждой группе: , … ,….,…,. Теперь можем рассчитать общую среднюю: где
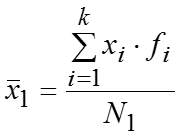
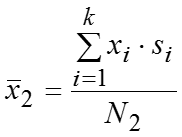
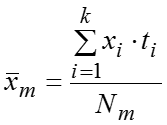
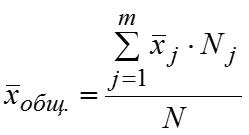
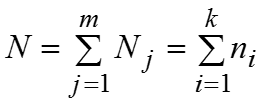
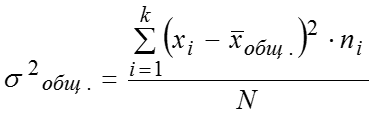
Тогда общая дисперсия измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию (действующих в данной совокупности). Межгрупповая дисперсия , где – групповые средние и – численности по группам. Межгрупповая дисперсия как отклонение групповой средней от общей средней характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака–фактора, положенного в основание группировки.
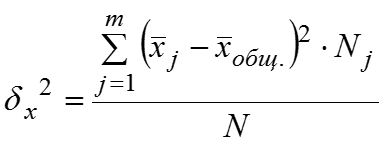
![]()
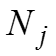
Рассчитаем значения дисперсий в каждой группе – (частных) групповых дисперсий: , .. ,.. , .. или по общей формуле , где – частоты при i = 1,2,….k в каждой j–той группе. Теперь можем рассчитать значение внутригрупповой дисперсии: , которая представляет собой среднюю арифметическую из (частных) групповых дисперсий и отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака–фактора, положенного в основание группировки.
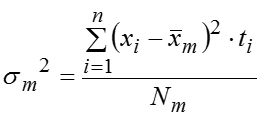
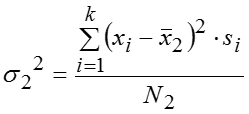
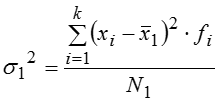
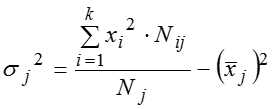
![]()
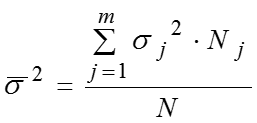
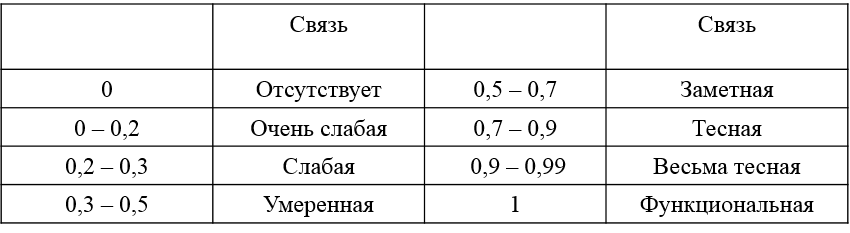
Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий: – правило сложения дисперсий. Эмпирический коэффициент детерминации позволяет найти долю межгрупповой дисперсии в общей дисперсии, показывает долю общей вариации изучаемого признака, обусловленную вариацией группировочного признака. Эмпирическое корреляционное отношение характеризует влияние признака, положенного в основание группировки, на вариацию результативного признака:
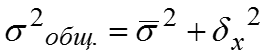
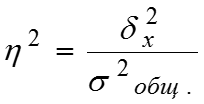
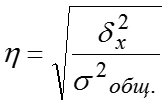
![]()
![]()
Пример.

![]()
![]()
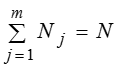
![]()
![]()
тыс.руб Межгрупповая дисперсия дает значение вариации величины пенсии, обусловленной различием в местах проживания: Средняя из групповых дисперсий дает значение случайной вариации величины пенсии, обусловленной всеми факторами, кроме места проживания:
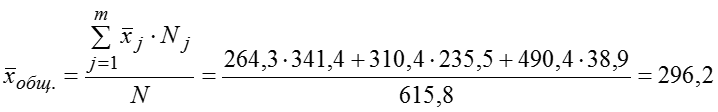
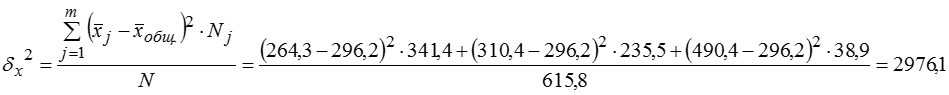
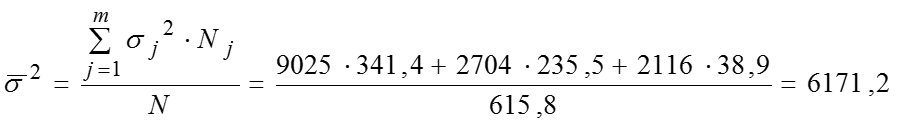
Тогда общая дисперсия, которая дает значение вариации величины пенсии под влиянием всех факторов: Рассчитаем значение эмпирического коэффициента детерминации: Итак, дисперсия пенсионных пособий зависит от места проживания на 32,5%, остальные 67,5% определяются множеством других факторов (занятость, стаж, профессия и т.п.). Эмпирическое корреляционное отношение, значит, существует заметная связь между местом проживания и размером ежемесячного пенсионного пособия.
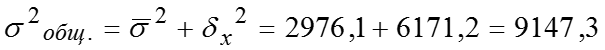
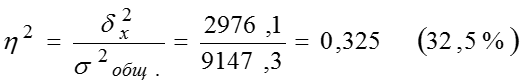
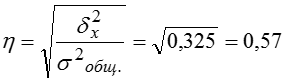
Группировочный признак не влияет на вариацию значений результативного Пример
Результативный признак меняется только в зависимости от группировного, влияние прочих факторных признаков равно 0
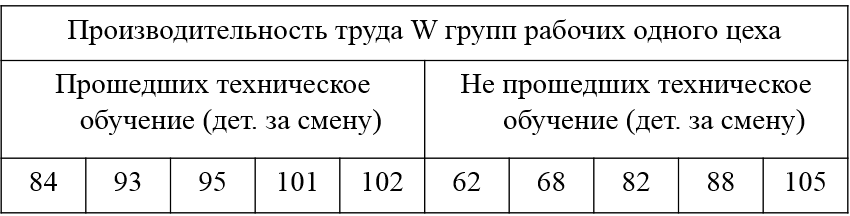
Групповые средние: дет. за смену и дет. за смену. Общая средняя: дет. за смену. Групповые дисперсии: Общая дисперсия
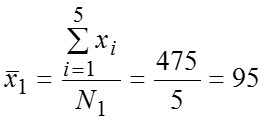
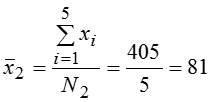
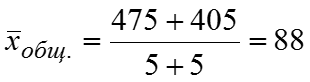
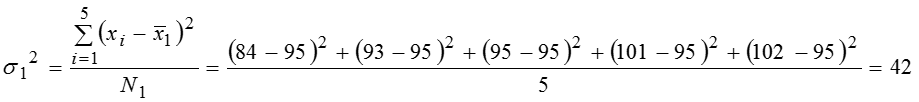
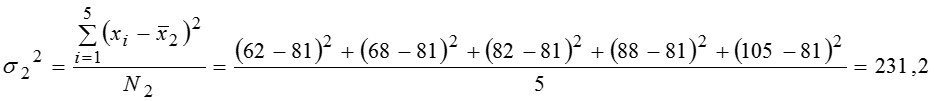
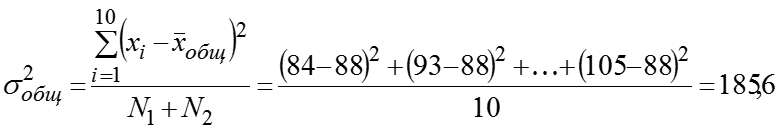
Или рассчитаем общую дисперсию с помощью средней из групповых дисперсий и межгрупповой дисперсии:
![]()
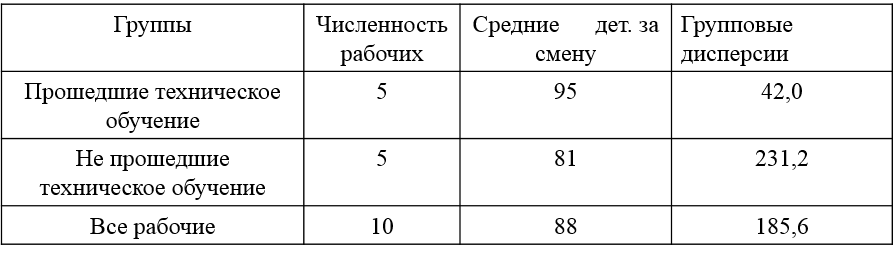
![]()
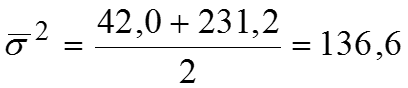
Средняя из групповых дисперсий
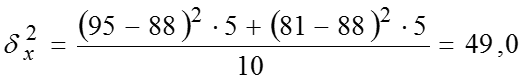
Межгрупповая дисперсия:
Тогда общая дисперсия по правилу сложения дисперсий:
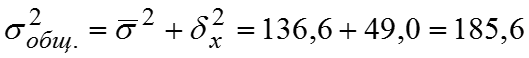
Найдем значение эмпирического корреляционного отношения: , значит вариация производительности труда W рабочих на 26,4% зависит от прохождения технического обучения и на 73,6% от неучтенных факторов. Итак, связь значений результативного признака с факторным слабая. Дисперсии доли для альтернативного признака – варианты значений признака в каждой группе статистической совокупности. Пусть – доля тех единиц совокупности в i–той группе, для которых , – доля тех единиц i–той группы совокупности, для которых . Известно, что , тогда внутригрупповая дисперсия доли
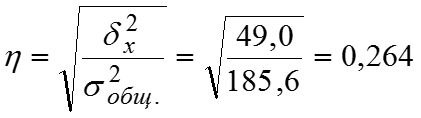
![]()
![]()
![]()
![]()
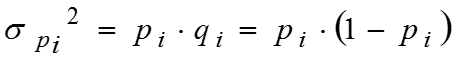
средняя из внутригрупповых дисперсий где – численность единиц в отдельных группах совокупности. Межгрупповая дисперсия где – доля изучаемого признака во всей совокупности.
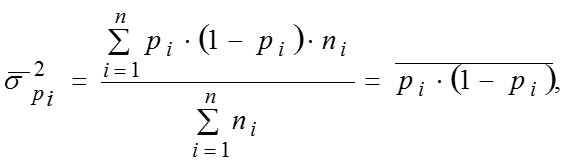
![]()
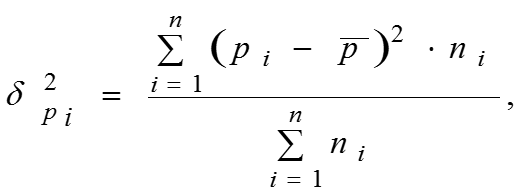
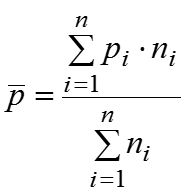
Общая дисперсия: или – теорема сложения дисперсий доли признака. Пример
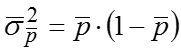
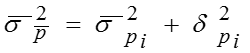
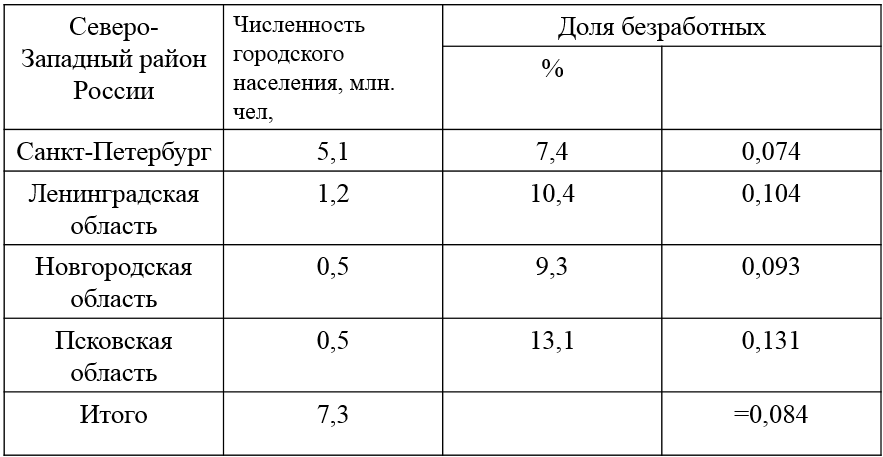
![]()
![]()
![]()
Общая дисперсия – по формуле для общей дисперсии доли. Групповые дисперсии: ;
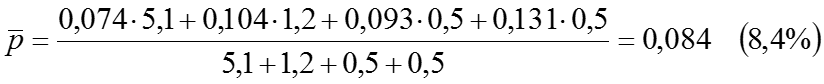
![]()
![]()
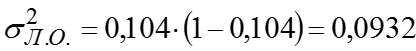
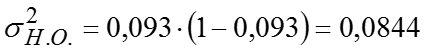
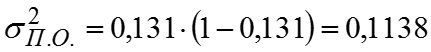
Средняя из групповых дисперсий
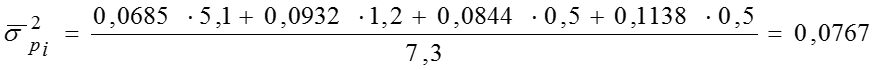
Межгрупповая дисперсия
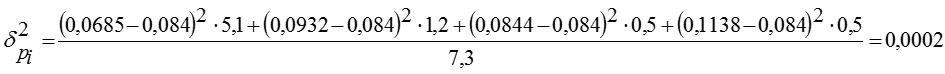
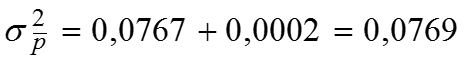
Теперь общая дисперсия по теореме сложения дисперсий. Эмпирическое корреляционное отношение показывает, что связь вариации результативного признака с вариацией факторного признака очень слабая.
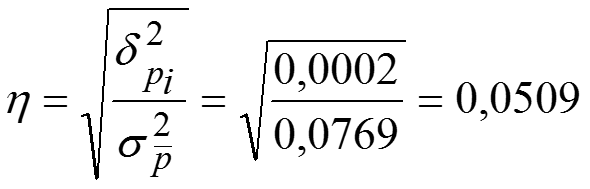
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.