Изучение взаимосвязи. Статистические методы классификации и группировки, анализа взаимосвязей и динамики социально-экономических явлений

4 ПРАКТИЧЕСКАЯ РАБОТА  5.

Изучение взаимосвязи. Статистические методы классификации и группировки, анализа взаимосвязей и динамики социально-экономических явлений.

Изучите примеры решения на стр. 203-214, решите задачи 9.26 -9.34, также задачи 9.14, 9.16, 9.18.

Методы изучения связи социальных явлений. Важной задачей статистики является разработка методики статистической оценки социальных явлений, которая осложняется тем, что многие социальные явления не имеют количественной оценки.

Количественная оценка связей социальных явлений осуществляется на основе расчета и анализа целого  ряда коэффициентов.

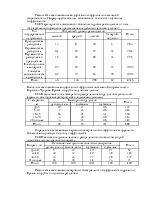
Коэффициент ассоциации и контингенции. Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации и контингенции. Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т.е. состоящим из двух качественно отличных друг от друга значений признака(например, хороший, плохой) (табл. 9.6)

Таблица 9.6

Таблица для вычисления коэффициентов  ассоциации и контингенции

Коэффициенты вычисляются по формулам:

ассоциации: 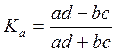 ;                                                                                   (9.21)

контингенции: 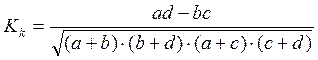                                        (9.22)

Коэффициент контингентов всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если К_а >0.5 или  K_k >0.3.

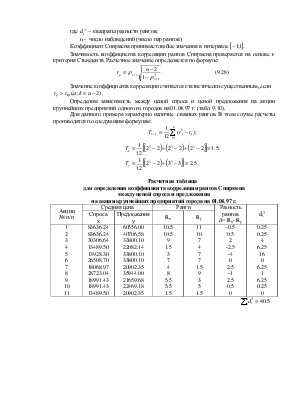
Пример. Исследовалось социально-демографическая характеристика случайных потребителей наркотиков в зависимости от их семейного положения в одном из регионов РФ(тыс.чел.). Результаты обследования характеризуются следующими данными:

Рассчитайте коэффициенты ассоциации и контингенции.

Решение:

=

=

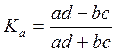
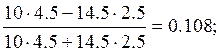
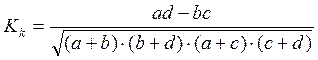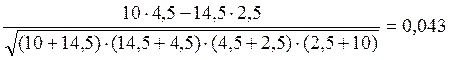
Вывод. Так как К_а >0.5 или  K_k >0.3, то потребление наркотиков случайными потребителями не зависит от их семейного положения.

Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициентов взаимной сопряженности Пирсена и Чупрова, которые вычисляются по следующим формулам:

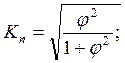
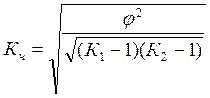 ,                            (9.23)

где - показатель взаимной сопряженности;

 - определяется как сумма отношений квадратов частот каждой клетки таблицы к                   произведению итоговых частот соответствующего столбца и строки минус 1;

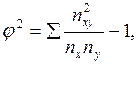
К₁ – число значений (групп) первого признака;

К₂ – число значений (групп) второго признака.

Чем ближе величины К_п и К_ч к 1, тем связь теснее .

Рассмотрим вспомогательную таблицу для расчетов коэффициента взаимной сопряженности (табл. 9.7).

Таблица 9.7

Вспомогательная таблица для расчета коэффициента взаимной сопряженности

1+.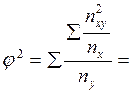

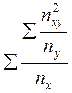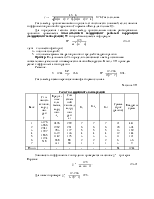
Пример. Исследовалась зависимость между оценкой уровня жизни респондентов Москвы и типов предприятия, на котором они работают. Данные, характеризующие опрос, приведены в табл. 9,8.

Необходимо определить коэффициенты взаимной сопряженности Пирсона и Чупрова.

Решение.

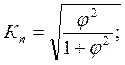
1+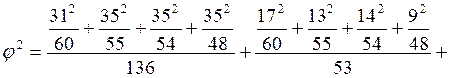

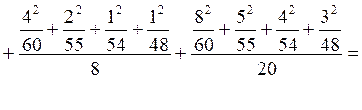
=0,636+0,249+0,047+0,100=1,032;

=1,032-1=0,032

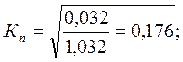
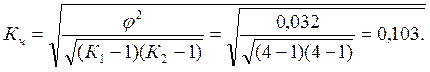
Вывод. Оценка уровня жизни респондентов не зависит от типа предприятия, на котором они работают.

В статистике существует модификации  коэффициента Пирсона, например через расчет - критерии.  Коэффициента  взаимной сопряженности (К_п)  вычисляется по формуле