Статистическое изучение корреляционных взаимосвязей. Этапы статистического изучения связи

Лекция модуль 4

Статистическое изучение корреляционных взаимосвязей

Социально–экономические явления представляют собой результат одновременного воздействия большого числа причин. Значит, при изучении этих явлений необходимо выявлять главные, основные причины, абстрагируясь от второстепенных.

Этапы статистического изучения связи:

1) качественный анализ изучаемого явления (в основе – анализ природы социального или экономического явления методами экономической теории, социологии, экономики);

2) построение модели связи (в основе – методы статистики: группировки, средние величины, таблицы и т.д.);

3) интерпретация результатов (в основе – качественные особенности изучаемого явления).

Признаки, обуславливающие изменение других, связанных с ним признаков, называются факторными.

Признаки, изменяющиеся под воздействием факторных признаков, являются результативными.

Взаимосвязь между отдельными признаками может быть:

 

Функциональная                    Стохастическая

(выявляется при массовом наблюдении как                              статистическая закономерность)

                                                       

Корреляционная

(изменение среднего значения

                                           результативного признака                                                                                     

                                           обусловлено изменением                                                                                                

                                           факторных признаков)

Корреляционная связь

 

                Множественная          Частная 

                    Парная

                                                                                                 

Прямая            Обратная

 

Линейная          Нелинейная

При изучении корреляционных связей решаются задачи:

1) выявление наличия связи между изучаемыми признаками (приведение параллельных данных, аналитические группировки, графический метод, корреляционные таблицы);

2) измерение тесноты связи (корреляционный анализ);

3) определение уравнения регрессии (регрессионный анализ).

Методы выявления корреляционной связи

Пример. Метод приведения параллельных данных.

завод	Основные производственные фонды, млн. руб.,	Валовой выпуск продукции, млн. руб.,	Знаки отклонения от средней величины
1	12	28	–	–
2	16	40	–	–
3	25	38	–	–
4	38	65	–	–
5	43	80	–	–
6	55	101	+	+
7	60	95	+	–
8	80	125	+	+
9	91	183	+	+
10	100	245	+	+
	520	1000

Коэффициент Фехнера (коэффициент корреляции знаков) – простейший показатель тесноты связи:

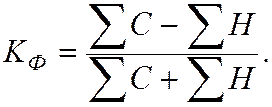
При совпадении знаков всех отклонений по каждому признаку 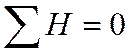 и , наличие прямой связи.

Если все знаки не совпадут, то 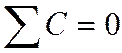 и , наличие обратной связи.

Если же 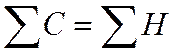, то , связь отсутствует.

Здесь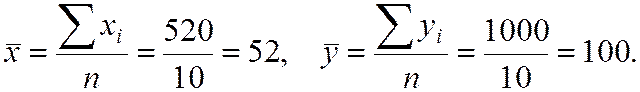  

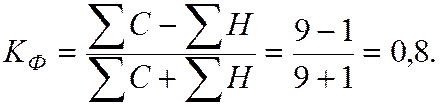
Сильная прямая зависимость.

Пример. Графический метод.

                                                                                                                

                                                                                                                                              

Прямая (положительная) регрессия

                                                                                                                

                                                                                                                                              

Обратная (отрицательная) регрессия

          ,

млн. руб.

         250

         200

         150

 

         100

 

           50

 

        10       20      30      40      50      60      70      80      90      100            млн. руб.,

Пример. Метод аналитических группировок.

Распределение уровня издержек обращения по группам предприятий оптовой торговли  в апреле 1995 г. (данные Российского статистического ежегодника)

Оптовый товарооборот, млн. руб.	Количество предприятий	Издержки обращения, % к оптовому товарообороту
Менее 25	9362	46,0
26 – 50	3633	26,5
51 – 100	3618	24,4
101 – 200	3261	23,0
201 – 500	3034	17,6
Более 500	3100	16,9

Пример. Метод корреляционных таблиц.

Таблица зависимости производительности труда  от стажа работы

Значение признака	Значение признака					Итого (число единиц)	Среднее значение по группам
	5	10	15	20
1	1	3	–		–	4	8,75
3	2	3	7		–	12	12,08
5	–	3	9		4	16	15,31
7	–	–	5		3	6	16,87
Итого (число единиц)	3	9	21		7		14,00

Если числа (частоты) расположены в клетках таблицы беспорядочно, то это говорит либо об отсутствии связи, либо о их незначительной зависимости.

Если частоты сконцентрированы ближе к одной из диагоналей, то это говорит о наличии зависимости (линейной или обратной).

Измерение тесноты связи

Пример.

Распределение 80 хозяйств по урожайности зерновых  и себестоимости 1 ц зерна

Урожайность зерновых, ц/га,	Себестоимость 1 ц зерна, руб.,				Итого (число хозяйств)	Средняя себестоимость 1 ц зерна по группам, руб.
	До 30 (=25)	30 – 40 (=35)	40 – 50 (=45)	50 – 60 (=55)
До 15	–	–	–	2	2	55,0
15 – 17	–	1	2	3	6	48,3
17 – 19	–	–	7	1	8	46,2
19 – 21	–	8	8	–	16	40,0
21 – 23	2	20	12	–	34	37,9
23 – 25	1	8	1	–	10	35,0
Свыше 25	3	1	–	–	4	27,5
Итого (число хозяйств)	6	38	30	6

Распределение частот в таблице не случайно, можно предположить, что между  и  существует стохастическая связь. Так как видна зависимость значений  от , то существует обратная корреляционная зависимость.

Измерим тесноту этой связи с помощью эмпирического корреляционного отношения: 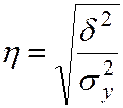, где межгрупповая дисперсия результативного признака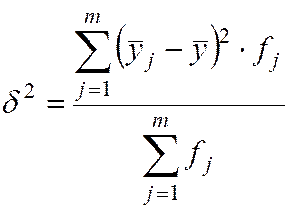

и общая дисперсия 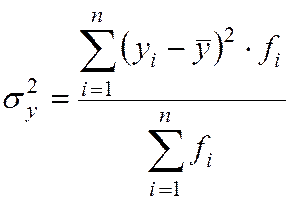, где m – число групп по факторному признаку x;

n – число единиц совокупности;

 – средние значения результативного признака по группам;

 – общее среднее значение результативного признака;

 – индивидуальные значения результативного признака;

 – частота в j – й группе x;

 – частота в i – й группе y.

.

.

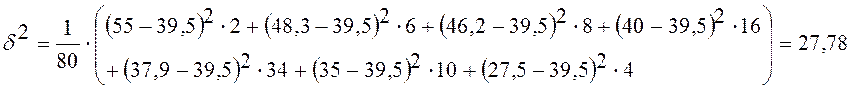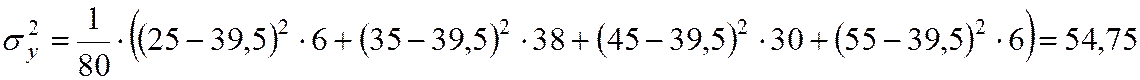Тогда эмпирический коэффициент детерминации

,

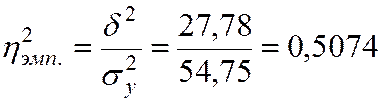Тогда эмпирическое корреляционное соотношение

.

Теснота связи выше средней, поэтому можно сделать вывод о наличии существенной обратной связи между урожайностью и себестоимостью зерна.

Нахождение уравнения регрессии между двумя признаками на основе метода наименьших квадратов и метода группировки

Аналитически парная регрессия может быть описана уравнениями:

· прямой ;

· параболы 2–го порядка  ;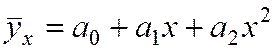

· гиперболы 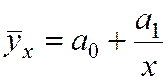 и т.д.

Из условия 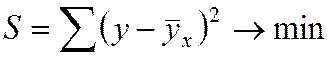получаем систему нормальных уравнений для определения коэффициентов в уравнении регрессии:

1) для линейной зависимости:

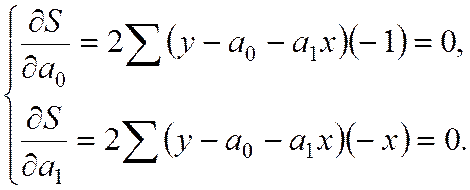
Откуда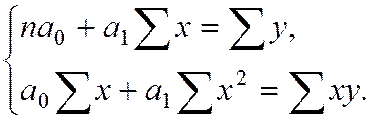 

Для сгруппированных данных:

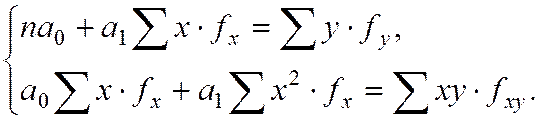
2) для параболической зависимости:

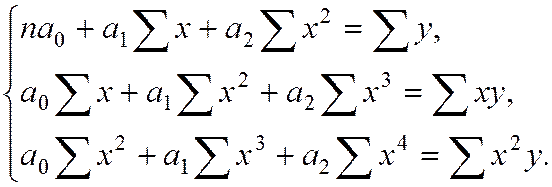
Для сгруппированных данных:

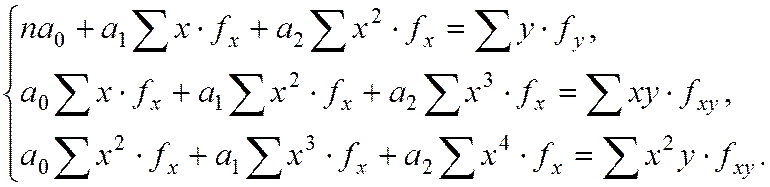
Расчет параметров упрощается, если:

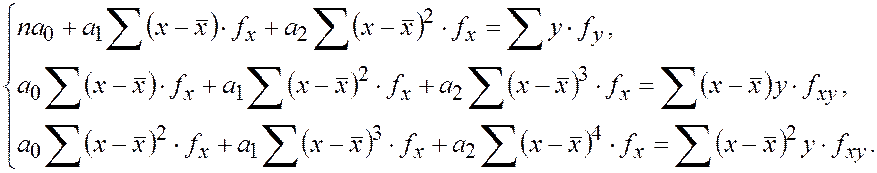
Тогда система примет вид:

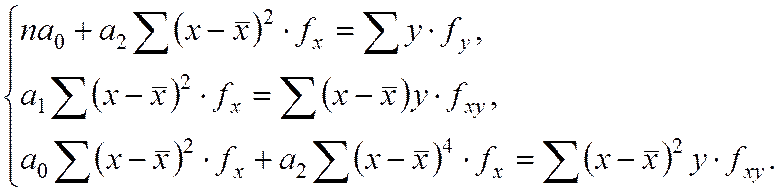
3) для гиперболической зависимости:

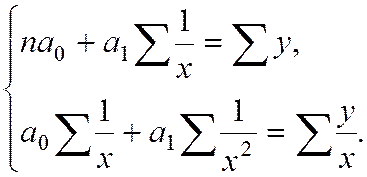
Для сгруппированных данных:

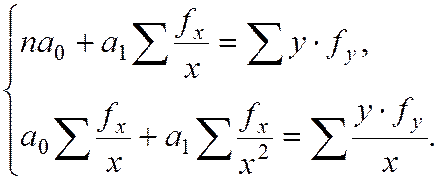
Множественная (многофакторная) регрессия

1)  линейная

2)  степенная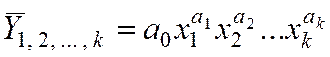

3)  показательная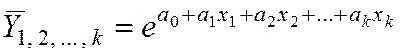

4)  параболическая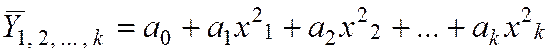

5)  гиперболическая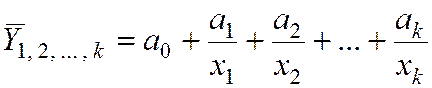

Изучение множественной корреляционной зависимости начинается с анализа матрицы парных коэффициентов корреляции, что позволяет произвести отбор факторов, включаемых в модель множественной зависимости

.

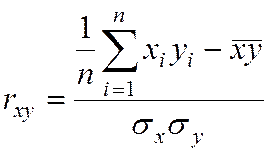Матрица имеет следующий вид:

Признак	Y			…
Y	1			…
		1		…
			1	…
…	…	…	…	1	…
				…	1

Анализ первой строки матрицы позволяет выявить те факторы, у которых степень тесноты связи с результативным показателем Y значительна, а поэтому они могут быть включены в модель.

Однако, возможна тесная зависимость между отдельными факторными признаками, включенными в модель (мультиколлинеарность), что приводит к искажению величины параметров модели, которые имеют тенденцию к завышению, и, следовательно, изменяют смысл экономической интерпретации коэффициентов регрессии.

Чтобы исключить мультиколлинеарность, требуется выполнение следующих условий:

если приведенные неравенств (или хотя бы одно из них) не выполняются, то исключается тот фактор  или , связь которого с результативным признаком Y будет менее тесной.

Далее измеряется степень тесноты связи между Y и факторными признаками  как совокупный коэффициент

корреляции: 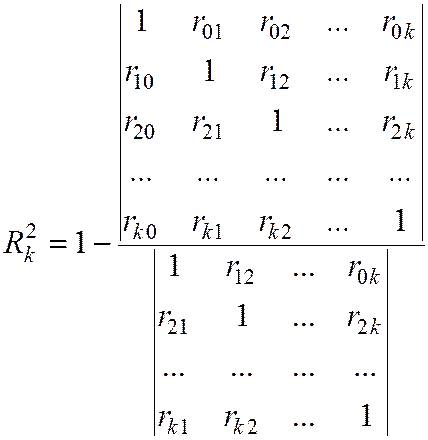 или коэффициент детерминации.

Величина R изменяется от 0 до 1 и не может быть меньше, чем любой