Другие предметы \ Статистика

Выборочное наблюдение. Предпосылки применения несплошного наблюдения в статистических исследованиях

Страницы работы

24 страницы (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

МОДУЛЬ 3

3.1. ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ

Предпосылки применения несплошного наблюдения в статистических исследованиях. Виды несплошного наблюдения, место выборочного наблюдения. Объективные отличия генеральной и выборочной совокупности как важнейшая причина ошибки репрезентативности результатов выборки. Способы отбора единиц в выборку. Виды выборки, правила их подготовки и проведения. Повторный и бесповторный отбор. Средняя ошибка выборки средней величины и доли. Определение необходимой численности выборки при различных способах отбора в выборку. Малая выборка: особенности проведения и оценки ее результатов. Распространение результатов выборочного наблюдения на генеральную совокупность.

Выборочное наблюдение – _______________________________________

Таким образом, из генеральной совокупности формируется в соответствии с принципами теории выборочного метода выборочная совокупность (выборка).

Принципы: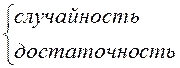

Репрезентативность – представительность выборки в отношении тех признаков, которые изучаются или оказывают существенное влияние на формирование сводных обобщающих характеристик.

Ошибки регистрации: _________________________________________

Ошибки репрезентативности: ___________________________________

____________________________________________________________________________________________________________________________________

Значение ошибки репрезентативности определяется по формулам, которые зависят от вида, метода и способа формирования выборочной совокупности.

По виду: _______________________________________________________

По методу отбора: ______________________________________________

Способ отбора определяет процедуру выборки единиц из генеральной совокупности.

Выборка может быть: собственно–случайная; механическая; типическая; серийная; комбинированная.

Собственно-случайная выборка __________________________________

____________________________________________________________________________________________________________________________________

Механическая выборка _________________________________________

______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

При типической выборке _______________________________________

При серийной (гнездовой) выборке ______________________________

Моментные выборочные обследования – _________________________

Одноступенчатый и многоступенчатый отбор – ____________________

Комбинированная – ____________________________________________

Символы основных характеристик параметров генеральной и выборочной совокупностей

Характеристики	Генеральная совокупность	Выборочная совокупность
Объем совокупности (численность единиц)
Численность единиц, обладающих обследуемым признаком
Доля единиц, обладающих обследуемым признаком
Средний размер признака
Дисперсия количественного признака
Дисперсия доли

Ошибка выборки

Ошибка выборки (ошибка репрезентативности) – это ________________

____________________________________________________________________________________________________________________________________

· для средней количественного признака

· для доли (альтернативного признака)

Средняя ошибка выборки зависит от степени варьирования изучаемого признака. В теореме П.Л. Чебышева доказано, что величина ошибки не превышает , где средняя ошибка выборки: .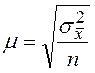

Соотношение между дисперсиями генеральной и выборочной совокупностей выражается формулой:, тогда средняя ошибка выборки: .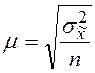

А.М. Ляпунов доказал, что распределение выборочных средних (а следовательно, и их отклонений от генеральной средней) при достаточно большом числе независимых наблюдений приближенно нормально при условии, что генеральная совокупность обладает конечной средней и ограниченной дисперсией: 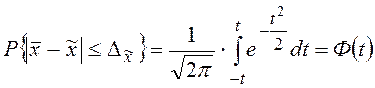. Здесь предельная ошибка выборки 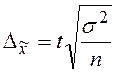дает возможность выяснить, в каких пределах находится величина генеральной средней.

Значения этого интеграла для различных значений коэффициента доверия вычислены и приводятся в таблицах:

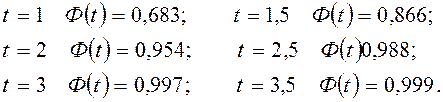
Зная выборочную среднюю величину признака, и предельную ошибку выборки, можно определить границы, в которых заключена генеральная средняя: . Аналогично для генеральной доли: .

Предельная ошибка выборки для некоторых способов формирования выборочной совокупности

Метод отбора Вид выборки	Повторный		Бесповторный
Метод отбора Вид выборки	Для средней	Для доли	Для средней	Для доли
Собственно-случайная и механическая
Типическая
Серийная
Комбинированная			, - число единиц, взятое в выборку из серий.

Необходимый объем выборки для некоторых способов формирования выборочной совокупности

Виды выборочного наблюдения	Повторный отбор	Бесповторный отбор
Собственно-случайная выборка: а) при определении среднего размера признака б) при определении доли признака
Механическая выборка	То же	То же
Типическая выборка: а) при определении среднего размера признака б) при определении доли признака
Серийная выборка: а) при определении среднего размера признака б) при определении доли признака

Способы распространения характеристик выборки на генеральную совокупность:

Способ прямого пересчета ______________________________________

____________________________________________________________________________________________________________________________________

Способ поправочных коэффициентов _____________________________

__________________________________________________________________

Задания для самостоятельной работы

Задача 1. Проведено выборочное тестирование студентов факультета по экономическим дисциплинам. Численность факультета 850 студентов, объем выборки, сформированной методом бесповторного отбора – 24 студента. Результаты тестирования приведены в таблице.

№ пп	Оценка (в баллах)	№ пп	Оценка (в баллах)	№ пп	Оценка (в баллах)	№ пп	Оценка (в баллах)
1	107	7	110	13	93	19	85
2	90	8	103	14	100	20	120
3	114	9	120	15	121	21	89
4	88	10	96	16	110	22	100
5	117	11	122	17	135	23	126
6	90	12	94	18	99	24	116

По этим данным определить выборочные средний балл, дисперсию и стандартное отклонение. Вычислить ошибку выборки, найти границы доверительного интервала, в котором окажется средняя генеральной совокупности с вероятностью 0,8 и 0,97.

Каждому студенту использовать свой набор исходных данных. Для этого ко всем значениям колонки «Оценка» прибавить число