Показатели вариации и анализ ее частотных распределений. Среднее квадратическое отклонение, относительное линейное отклонение

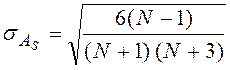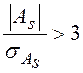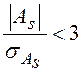оценка степени существенности этого показателя дается с помощью средней квадратической ошибки, которая зависит от объема наблюдений и рассчитывается по формуле: , если , то асимметрия существенна и распределение признака в генеральной совокупности не является симметричным. Если , то асимметрия несущественна, ее наличие может быть объяснено влиянием различных случайных обстоятельств.

Для симметричных распределений рассчитывается показатель эксцесса 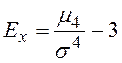, который является показателем островершинности кривой распределения.

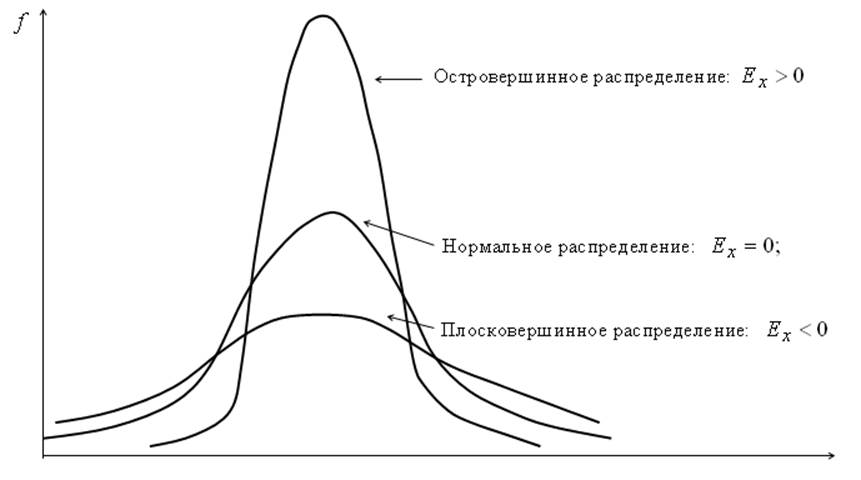
Среднеквадратическая ошибка эксцесса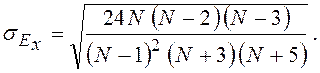  

Точечное оценивание числовых характеристик значений признака

Кривая распределения характеризует теоретическое распределение, т.е. то распределение, которое получилось бы при полном погашении всех случайных причин, искажающих основную закономерность.

Начальный момент первого порядка  называется выборочным средним, выборочным математическим ожиданием или средним арифметическим выборки. Математическое ожидание характеризует положение распределения на оси X.

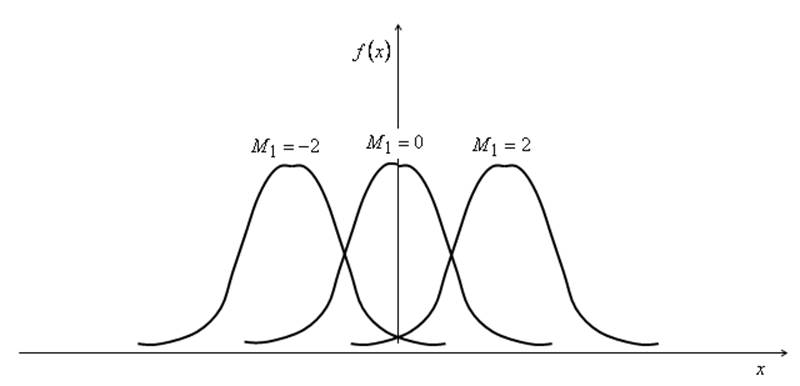
Рис. 1. Положение кривой распределения с разными значениями .

Дисперсия и среднеквадратическое отклонение являются характеристиками рассеяния, или разброса значений признака .

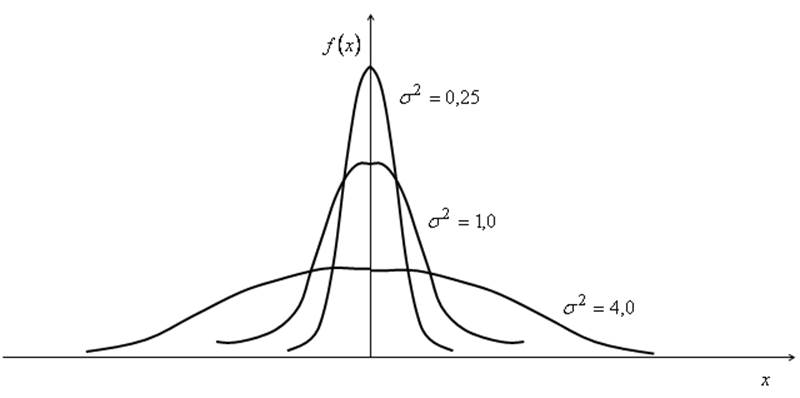
Рис. 2. Кривые распределения с различными значениями дисперсии и одинаковыми .

К другим характеристикам положения распределения значений признака относятся мода  и медиана. Их взаимное расположение помогает характеризовать асимметричность распределения.

Теоретические кривые распределения

Виды теоретического распределения: нормальное, логарифмически нормальное, биномиальное, Пуассона, Шарлье и др.

Чаще всего в качестве теоретического распределения используется нормальное распределение плотности вероятностей: .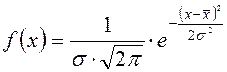

Свойства нормального распределения

1. 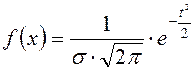  – четная функция, график симметричен относительно прямой , так как ;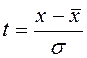

2.  ;  

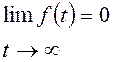3.  ,   ;

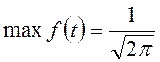4.  точки перегиба при ;

5.  если кривая распределения является суммой двух кривых, каждая из которых следует нормальному закону, то она также следует нормальному закону;

6. 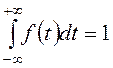 , как интеграл Пуассона, где 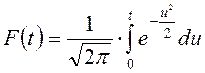 – нормированная функция Лапласа. Значения интегральной функции Лапласа определяются по таблицам:

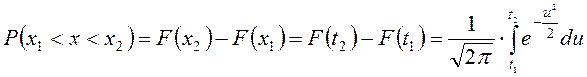, где .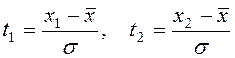

Параметры  и влияют на вид нормальной кривой. Если  не меняется, а изменяется только , то:

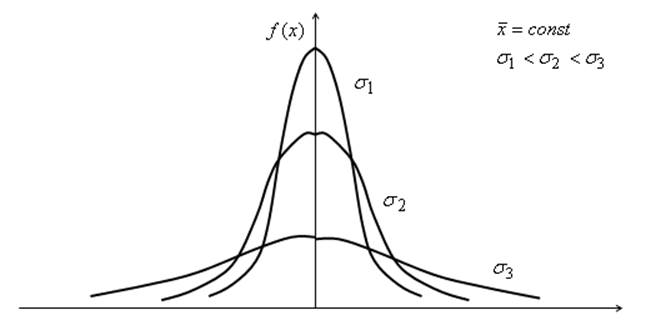
1)   чем меньше , тем более вытянута вверх и сжата вдоль оси абсцисс кривая распределения;

2)   чем больше , тем более плоской и растянутой вдоль оси абсцисс становится кривая распределения.

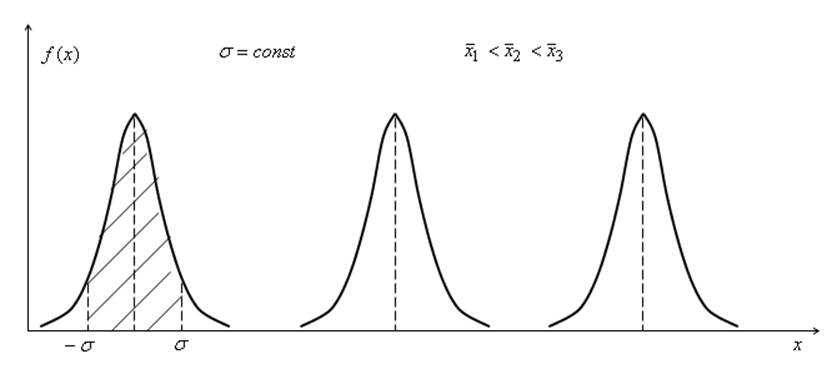
Если    остается неизменным, а  изменяется, то кривые нормального распределения имеют одинаковую форму, но отличаются друг от друга положением максимальной ординаты.

Порядок расчета теоретических частот кривой нормального распределения:

1)   по эмпирическим данным рассчитываем среднюю арифметическую ряда  и среднее квадратическое отклонение ;

2)   находим нормированное отклонение каждой варианты от средней арифметической: ;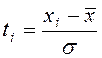

3)   по таблице распределения функции 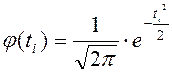 определяют ее значения;

4)   вычисляют теоретические частоты по формуле: 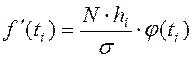. В случае, когда вариационный ряд имеет равные интервалы, .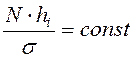

Пример.

Распределение призывников по росту (данные условные)

В данном случае 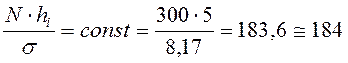 и за счет округлений при расчетах нет равенства сумм эмпирических и теоретических частот: 300 и 297.

Сравним на графике эмпирические и теоретические частоты, полученные на основе данных таблицы:

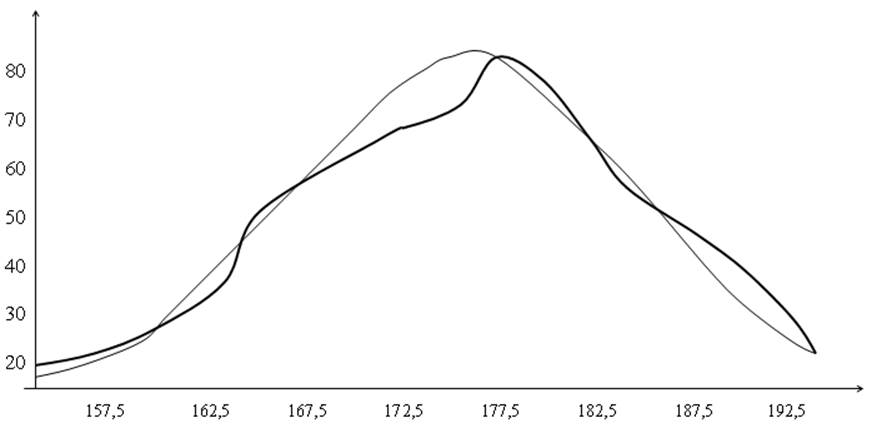
Близость значений этих частот очевидна, но объективная оценка может быть получена только с помощью критериев согласия.      

Распределение Пуассона

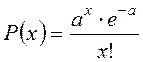, где  - вероятность того, что признак примет то или иное (дискретное: 0, 1, 2, 3, …) значение,  – средняя арифметическая ряда.

Порядок расчета теоретических частот кривой распределения Пуассона:

1)   по эмпирическим данным рассчитываем среднюю арифметическую ряда