Исследование заданного механизма. Определение формулы строения механизма, его класса и порядка

Санкт-Петербургский государственный аграрный университет

Кафедра  технической механики и гидравлики

РАСЧЁТНО – ПОЯСНИТЕЛЬНАЯ  ЗАПИСКА

     К  КУРСОВОМУ ПРОЕКТУ

      ПО ТЕОРИИ  МЕХАНИЗМОВ  И  МАШИН

Тема  проекта:

“Исследование  заданного механизма ”

Задание  № ….

Вариант  № ….

Выполнил:    студент гр.

( Фамилия, И.О. )

Руководитель: _____________ 

(……………….)

Пушкин,  2009 г.

СОДЕРЖАНИЕ:

1.  Структурный анализ механизма

1.1  Схема заданного механизма                                                                                3

1.2  Определение степени подвижности механизма                                                4

1.3  Разложение механизма на структурные группы Ассура, определение их класса, порядка и вида                                                                                    4

1.4   Определение формулы строения механизма, его класса и порядка               4

2.  Кинематическое исследование механизма4

2.1  Планы положений механизма                                                                             4

2.2  Планы скоростей механизма                                                                               5

2.3  Планы ускорений механизма                                                                              7

2.4  Диаграммы перемещений, скоростей и ускорений ползуна                           10

Литература                                                                                                          12

1.   Структурный  анализ механизма 

1.1  Схема заданного механизма

 

Рис. 1

Параметры	Букв. обознач.	Величина
Ход поршня,  (м)	Нс	0.08
Отношение АВ:ВС,	λ	0.25
Положение ц.м. шутуна, (м).	LBS2	0.07
Диаметр цилиндра, (м).	D	0,075
Максимальное давление в целиндре, (Н/м2)	Pmax	10*105
Масса шатуна, (кг)	m2	2,5
Масса поршня, (кг).	m3	5
Момент инерции крив., (кг.м2)	IS1	0,004
Момент инер. шатуна, (кг.м2)	IS2	0,0125
Угловая скорость, (рад/с)	w1	50
Коэффициент неравномерности	δ	0.17
№ положения для силового расчета	-	4 и 11

1.2  Определение степени подвижности механизма

Степень подвижности механизма определяем по формуле Чебышева:

где:   n – число подвижных звеньев;

p ₅ – число кинематических пар 5–го класса;

 p ₄ – число кинематических пар 4–го класса.

Степень подвижности заданного механизма равна:

Значит, для однозначного определения положения всех звеньев достаточно задать положение только одного звена механизма.

1.3  Разложение механизма на структурные группы Ассура, определение  их класса, порядка и вида.

Из представленной схемы видно, что механизм состоит из механизма 1–го класса (звенья 0 и 1) и присоединённой  к нему  группы Ассура второго класса второго порядка.

1.4  Определение формулы строения механизма, его класса и порядка

Формула строения механизма имеет вид:

Класс и порядок механизма определяется по наивысшему классу группы Ассура, которая входит в его состав. Значит данный механизм – второго класса, второго порядка.

2.   Кинематическое исследование механизма

2.1  Планы положений механизма

Планы 12 положений механизма изображаются на первом листе чертежа курсового проекта. Они нужны для того, чтобы:

а) показать положение всех звеньев механизма в различные моменты времени, б) определить ход ползуна,

Построение проводим в масштабе. Под масштабом понимают отношение действительной длины звена в метрах, к длине звена на чертеже в мм, например: 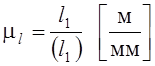  ; длину кривошипа на чертеже должна быть  (l₁) = 40¸70 мм.

Принимаем в нашем случае  (l₁) = 40 мм. Тогда масштаб длин будет:

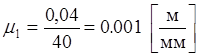
Теперь можно определить все остальные размеры на чертеже по формуле:                    

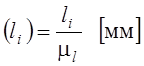
Эти размеры будут:

 

 

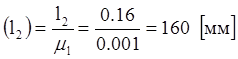
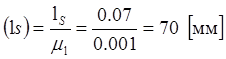
Далее чертим планы механизма в 12 положениях, используя рассчитанные длины и расстояния.

2.2  Планы скоростей механизма                                                                             

Планы скоростей механизма изображаются на первом листе чертежа. Они нужны для того, чтобы:

а) определить величину и направление скорости любой точки механизма в различные моменты времени, б) определить угловые скорости звеньев в различные моменты времени.

Построение планов скоростей проводим в соответствии с формулой, известной из теоретической механики:

                                                                 (1)

где:     – абсолютная скорость точки;

 – переносная скорость выбранного полюса;

 – скорость точки относительно выбранного полюса.

Для того, чтобы начертить планы скоростей, сначала нужно вычислить скорость точки В кривошипа АВ. Эту скорость определяем по формуле:

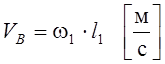
где:     – модуль скорости точки В;

 – заданная угловая скорость движения кривошипа, ;

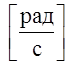 – заданная длина кривошипа (в метрах).

В нашем случае:

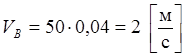
Эту скорость нужно показать на чертеже в виде вектора, перпендикулярного кривошипу АВ и имеющего длину  мм .  Принимаем  мм . Тогда масштаб будущего плана скоростей  будет:

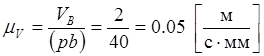
Для определения скорости точки С записываем векторные уравнения вида (1):

               

V_{B +} V_CB = V_C + V_CCo                                                  

                                                                                        _{+       ┴BC          0           II x}

                                                                                        ^{+        ?                             ?}

 

Далее строим планы скоростей для каждого положения механизма, используя в каждом из них вектор  и векторные уравнения (2) . После построения всех 12 планов скоростей определяем величины скоростей всех характерных точек механизма, используя формулу:

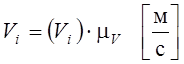
где:     – длина вектора скорости характерной точки на плане скоростей;

 – масштаб плана скоростей, вычисленный ранее.

Угловые скорости вращательного движения звеньев 2,  можно рассчитать по формуле

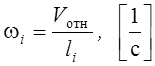
где:      –  относительная скорость, полученная из плана скоростей,;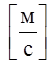

 – длина соответствующего звена, [м].

Результаты вычислений  и  сводим в таблицу 1.

Таблица 1

	0	1	2	3	4	5	6	7	8	9	10	11
VB  (м/с)	2	2	2	2	2	2	2	2	2	2	2	2
VC   (м/с)	0	0,78	1,5	2	1,95	1,2	0	1,2	1,95	2	1,5	0,78
VCB  (м/с)	2	1,75	1	0	1	1,75	2	1,75	1	0	1	1,75
VS2  (м/с)	0,95	1,25	1,7	0	1,9	1,4	0,95	1,4	1,9	0	1,7	1,25
w2  (1/с)	12,5	10,9	6,25	0	6,25	10,9	12,5	10,9	6,25	0	6,25	10,9

2.3  Планы ускорений механизма

Планы ускорений механизма изображаются на первом листе чертежа. Они нужны для того, чтобы:

а) определить величину и направление ускорения любой точки механизма в различные моменты времени, б) определить угловые ускорения звеньев в различные моменты времени.

Построение планов ускорений проводим в соответствии с формулами, известными из теоретической механики:

 ,                                                              (4)

 где:

 – если относительное движение является вращательным,            (5)

– если в относительном движении одним из составляющих

                            является поступательное движение (кулиса).                              (6)

            В этих формулах:

   –  абсолютное ускорение точки;

  – полное относительное ускорение точки;

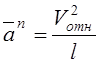 – нормальное относительное ускорение точки;                              (7)

  –  тангенциальное относительное ускорение точки;

    – ускорение Кориолиса;                                                     (8)

 – относительное ускорение точки вдоль оси кулисы;

Для того, чтобы изобразить планы ускорений, сначала нужно вычислить