Дійсні числа та дії над ними. Вiдсотковi розрахунки. Як досягти успiху у сучасному суспiльствi

Підставимо замість  S_п величину кінцевої суми - 1600, замість  S величину початкового вкладу - 1000 і замість п кількість місяців – 12. Отримаємо і розв’яжемо рівняння: 1600 = 1000(1 + 0,01·12·р); 1600 = 1000 + 120р; 120р = 600; р = 5. Отже, відсоткова ставка повинна становити 5% на місяць.

У банках для деяких видів вкладів (так званих термінових вкладів, які не можна взяти раніше, ніж, скажімо, через рік) прийнята така система нарахування: за перший рік перебування вкладеної суми в банк на рахунку нараховується, наприклад, 20% від неї. Якщо наприкінці року вкладник не зняв з рахунку ці гроші – «проценти» як їх звичайно називають, то вони приєднуються до вкладеної суми і наприкінці другого року 20% нараховуються уже із збільшеної суми. В даному випадку «відсотки» нараховуються на «відсотки». Для виведення формули складних відсотків розв’яжемо таку задачу: початковий внесок в банк дорівнює S грн. За рік нараховується р відсотків. Обчислити суму внеску через п років.

Через 1 рік сума внеску буде: S + S · 0,01р = S(1 + 0,01р).

Через 2 роки сума внеску буде: S(1 + 0,01р) + S(1 + 0,01р) · 0,01р =

S(1 + 0,01р) · (1 + 0,01р) = S(1 + 0,01р)².

Через 3 роки сума внеску буде: S(1 + 0,01р)² + S(1 + 0,01р)² · 0,01р =

S(1 + 0,01р)² · (1 + 0,01р) = S(1 + 0,01р)³.

Тобто через п років сума внеску буде: S(1 + 0,01р)^п.

Формула складного відсоткового зростання (або формула складних відсотків) Sn  =S(1  0,01p) п  Sn – кінцева сума,  S – сума початкового внеску, р – річні відсотки, п – кількість років перебування вкладу.

Слайд 7

Відмінність простого відсоткового зростання і складного відсоткового зростання полягає в тому, що при простому зростанні відсоток кожний раз обчислюють, виходячи з початкового значення величини, а при складному зростанні відсоток обчислюється від попереднього значення. Ця формула використовується не тільки в банковій діяльності, але і в будь-якій ситуації, коли розглядувана величини збільшується або зменшується на певну кількість відсотків, рахуючи від її попереднього значення.

Задача. Початковий внесок в ощадбанк дорівнює 300 доларів, за рік нараховується 3%. Знайти суму внеску через 5 років.

S = 300(1 + 0,01 · 3)⁵ = 300 · 1,03⁵ ≈ 300 · 1,159 ≈ 348 (доларів)

А тепер розглянемо ще декілька видів задач на відсотки, які уже не можна віднести до виду найпростіших.

Слайд 8

Задачі,  що розв’язуються арифметичним способом Ціну товару спочатку знизили на 20%, потім нову ціну знизили ще на 15% і, нарешті, після перерахунку провели зниження ще на 10%. На скільки відсотків всього знизили початкову ціну товару?

 

Розв’язання.

Цю задачу простіше розв’язати арифметично, не складаючи рівняння.

1.  Нехай початкова ціна товару х грн.

2.  Після першої знижки ціна товару буде: х – 0,2х = 0,8х грн..

3.  Після другої знижки: 0,8х – 0,15 · 0,8х = 0,68х грн.

4.  Після третьої знижки: 0,68х – 0,1 · 0,68х = 0,612х грн.

5.  Всього ціна товару знизилася на:  х – 0,612х = 0,388х грн.

6.  Складемо пропорцію:   х – 100%

                                             0,388х – у%;

Звідси   у% = (0,388х · 100%) : х = 38,8%.

Відповідь. На 38,8%.

Слайд 9

Задачі,  в яких відомо, на скільки відсотків одне число більше (менше), ніж друге За кілограм одного товару і 10 кг другого заплачено 200 грн. Якщо при зміні цін перший товар подорожчає на 15%, а другий подешевшає на 25%, то за таку ж кількість цих товарів буде заплачено 182 грн. Скільки коштує кілограм кожного товару?

 

Розв’язання.

1.  Нехай вартість 1 кг першого товару х грн., а вартість 1 кг другого товару у грн..  

2.  Вартість 1 кг першого товару і 10 кг другого 200 грн:  х + 10у = 200.

3.  Вартість 1 кг першого товару після подорожчання: х + 0,15х = 1,15х.

4.  Вартість 1 кг другого товару після здешевлення: у – 0,25у = 0,75у.

5.  З умови задачі маємо систему: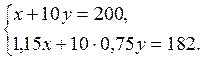 

6.  Розв’язавши систему рівнянь, маємо х = 80, у = 12.

Відповідь. 80 грн, 12 грн.

Слайд 10

Задачі на суміші (сплави) Змішали 30%-ний  розчин соляної кислоти з 10%-ним і отримали 600 г 15%-ного розчину. Скільки грам кожного розчину було взято?

 

Розв’язання.

1.  Нехай 30%-ного розчину взяли х грам, а 10%-ного - у грам.

2.  Тоді з умови задачі: х + у = 600.

3.  Якщо перший розчин 30%-ний, то в х грамах цього розчину міститься 0,3х грамів соляної кислоти. Якщо другий розчин 10%-ний, то в у грамах цього розчину міститься 0,1у грамів кислоти.

4.  В отриманій суміші міститься 600 · 0,15 = 90 грам кислоти, звідки маємо: 0,3х + 0,1у = 90.

5.  Складемо і розв’яжемо систему рівнянь: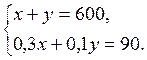

Отримаємо: х = 150, у = 600 – 150 = 450.

Відповідь. 150 г, 450 г.

Слайд 11

Задачі на розведення Із баку, наповненого спиртом, відлили частину спирту і долили до початкового об’єму водою, потім із баку відлили скільки літрів суміші, скільки першого разу відлили спирту, після чого в бакові залишилося 49 л чистого спирту. Скільки літрів спирту відлили з баку першого і другого разу, якщо в бакові містилося 64 л?

 

Розв’язання.

1.  Нехай першого разу відлили х літрів спирту. Тоді в бакові залишилося (64 – х) літрів спирту.

2.  Після того, як бак долили водою, в ньому стало 64 літри суміші