Отчёт
про педагогическую практику студентки
5 курса механико-математического факультета
Я проходила педагогическую практику с 27.09.2012 по 20.12.2012 г. в университете им. В.Н.Каразина на механико-математическом факультете. Была прикреплена к группе М-132, а именно к иностранным студентам Ильхаму Мухиеву и Марал Ходжагелдиевой. Дифференциальную геометрию группе М-132 преподаёт старший преподаватель Елена Алексеевна Шугайло. Иностранным студентам требовалась помощь в решении задач по дифференциальной геометрии.
Факультативные занятия проходили 2 раза в месяц.
27 сентября провела вместе со студенткой-практиканткой Проплёткиной Людмилой занятие на тему: «Производные и интегралы сложных функций».
11 октября провела занятие на тему: «Уравнения касательной и нормали для плоских кривых».
25 октября посетила занятие студентки-практикантки Проплёткиной Людмилы на тему: «Длина дуги кривой. Кривизна кривой».
8 ноября провела вместе со студенткой-практиканткой Проплёткиной Людмилой занятие на тему: «Эволюта и эвольвента».
22 ноября посетила занятие студентки-практикантки Проплёткиной Людмилы на тему: «Репер Френе».
6 декабря провела занятие на тему: «Кривизна и кручение пространственных кривых»
20 декабря провела вместе со студенткой-практиканткой Проплёткиной Людмилой занятие на тему: «Первая и вторая квадратичные формы».
Итого провела два занятия самостоятельно и три занятия со студенткой-практиканткой Проплёткиной Людмилой. Посетила два занятия Проплёткиной Людмилы. Всего было проведено семь факультативных занятий.
План-конспект факультатива на тему «Уравнение касательной и нормали для плоских кривых»
11.10.2012
Цели факультатива: вторичное осмысливание уже известных знаний, выработка умений и навыков по их применению.
Тип факультатива: факультатив закрепления знаний
Сегодня мы повторим тему «Уравнение касательной и нормали для плоских кривых» и научимся применять знания на практике.
Повторение теоретического материала:
1. Касательная к плоской линии
Касательной к линии L
в точке М называется прямая ![]() , с которой
стремиться совпасть секущая
, с которой
стремиться совпасть секущая ![]() , когда точка
, когда точка ![]() , оставаясь на L, стремится к М.
, оставаясь на L, стремится к М.
2. Уравнение касательной к плоской линии
Пусть МТ –
касательная к линии L в точке ![]() . Обозначим
текущие координаты точки N, лежащей на касательной, через Х,У. При любом
задании линии L уравнение касательной имеет вид:
. Обозначим
текущие координаты точки N, лежащей на касательной, через Х,У. При любом
задании линии L уравнение касательной имеет вид:
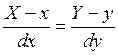 .
.
Если кривая задана уравнением в параметрической форме:
![]()
уравнение её касательной запишется так:
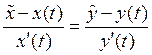 .
.
Если кривая задана
уравнением ![]() , то уравнение касательной запишется
так:
, то уравнение касательной запишется
так:
![]()
Если кривая задана
уравнением ![]() , то уравнение касательной запишется
так:
, то уравнение касательной запишется
так:
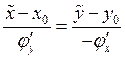
3. Уравнение нормали
Если кривая задана
параметрически ![]() , то уравнение нормали
имеет вид:
, то уравнение нормали
имеет вид:
![]()
Если кривая задана
явно ![]() , то уравнение нормали имеет вид:
, то уравнение нормали имеет вид:
![]()
Если кривая задана
неявно ![]() , то уравнение нормали имеет вид:
, то уравнение нормали имеет вид:
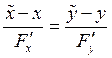 .
.
III. Применение знаний
Составить уравнение касательных:
1) 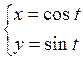
в точке 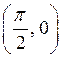 .
.
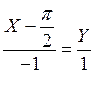
2) ![]()
![]()
3) 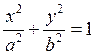 в точке (1,1).
в точке (1,1).
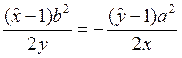
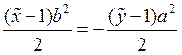 .
.
Составить уравнение нормали:
1) 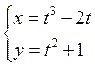 в точке
в точке ![]() .
.
![]()
2) ![]() в точке
в точке ![]() .
.
![]()
3) ![]() в точке
в точке 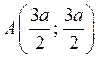 .
.
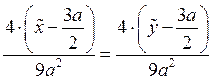 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.