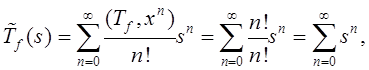 так как
так как
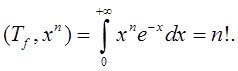
Таким
образом, ![]()
В случае финитной
регулярной формальной обобщенной функции ![]() можно
получить такую связь между ее преобразованием Лапласа и двухсторонним
преобразованием Лапласа функции f.
можно
получить такую связь между ее преобразованием Лапласа и двухсторонним
преобразованием Лапласа функции f.
Теорема 4.4. Пусть ![]() - финитная регулярная формальная
обобщенная функция, т.е.
- финитная регулярная формальная
обобщенная функция, т.е. ![]() измерима,
измерима, ![]() обращается в нуль вне
некоторого отрезка
обращается в нуль вне
некоторого отрезка ![]() ,
, ![]() и
и 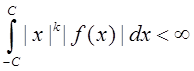 для
всех
для
всех ![]() . Рассмотрим классическое двухстороннее
преобразование Лапласа
. Рассмотрим классическое двухстороннее
преобразование Лапласа ![]() функции
функции ![]() и преобразование Лапласа
и преобразование Лапласа ![]() регулярной формальной
обобщенной функции
регулярной формальной
обобщенной функции ![]() , где
, где 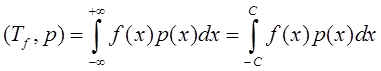 . Тогда радиус сходимости
степенного ряда
. Тогда радиус сходимости
степенного ряда ![]() равен бесконечности,
равен бесконечности, ![]() - целая функция и
- целая функция и ![]() для всех
для всех ![]() .
.
Доказательство.
Запишем
классическое преобразование Лапласа функции ![]() в
следующей форме:
в
следующей форме:
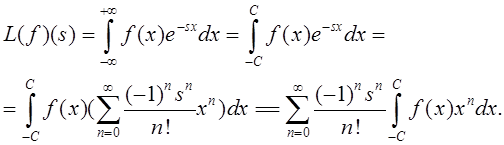
Изменение
порядка интегрирования и суммирования законно, так как 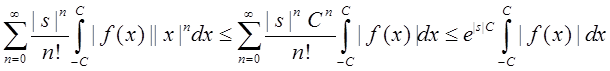 ,
,
![]() и возможно применение теоремы
Фубини. Таким образом,
и возможно применение теоремы
Фубини. Таким образом,

и
полученный степенной ряд сходится для всех ![]() .
Кроме того,
.
Кроме того,
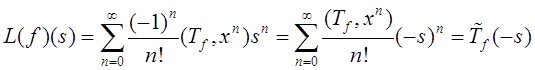 ,
, ![]() .
.
Теорема доказана.
Следующая теорема обобщает ситуацию, рассмотренную в примере 4.3.
Теорема 4.5. Пусть ![]() - регулярная формальная
обобщенная функция, причем
- регулярная формальная
обобщенная функция, причем ![]() , если
, если ![]() и
и 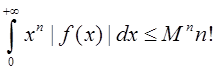 для
которого
для
которого ![]() . Тогда радиус сходимости
степенного ряда
. Тогда радиус сходимости
степенного ряда ![]() не меньше
не меньше ![]() , функция
, функция ![]() голоморфна в круге
голоморфна в круге 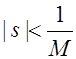 и
и ![]() для
всех
для
всех 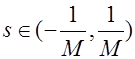 .
.
Доказательство.
Так
как  , то
, то
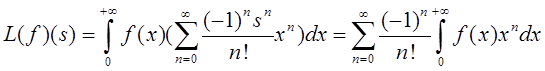 .
.
Изменение порядка интегрирования и суммирования законно, т.к.
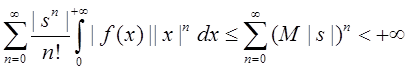 , если
, если
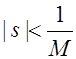 . Таким образом,
. Таким образом,
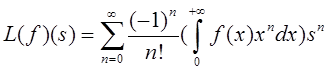
и
полученный степенной ряд сходится для всех 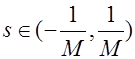 .
.
Теорема доказана.
Замечание. Отметим, что для функции f из теоремы 4.5 ее одностороннее и двухстороннее преобразование Лапласа совпадают.
Рассмотрим еще один пример.
Пример 4.6. Пусть ![]() Найдем 3 вида преобразования
Лапласа функции
Найдем 3 вида преобразования
Лапласа функции ![]() .
.
1. Классическое
двухстороннее преобразование Лапласа функции ![]() имеет
вид:
имеет
вид:
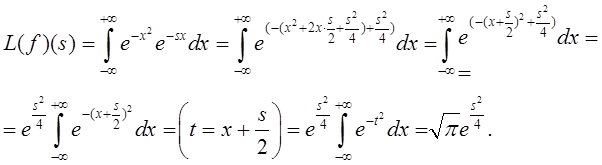
2. Преобразование
Лапласа функции ![]() как регулярной
формальной обобщенной функции:
как регулярной
формальной обобщенной функции:
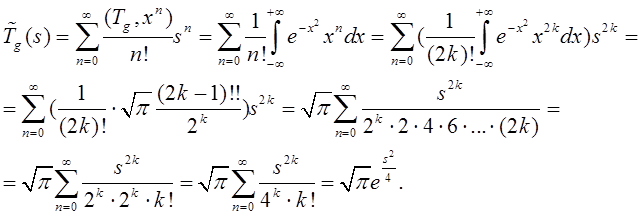
3. Преобразование
Лапласа функции ![]() как формального
степенного ряда:
как формального
степенного ряда:
Так как
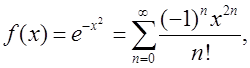 то
то 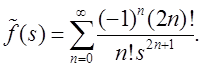
Мы видим, что ![]() для всех
для всех ![]() , но
, но ![]() существенно
отличается от классического двухстороннего преобразования Лапласа и связано с
классическим односторонним преобразованием Лапласа (см. §2).
существенно
отличается от классического двухстороннего преобразования Лапласа и связано с
классическим односторонним преобразованием Лапласа (см. §2).
Теперь получим следующее обобщение примера 4.6.
Теорема 4.7. Пусть f– регулярная
формальная обобщенная функция, причем 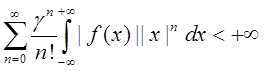 для
некоторого
для
некоторого ![]() . Тогда степенной ряд
. Тогда степенной ряд ![]() сходится при
сходится при ![]() и
и ![]() ,
,
![]() , где
, где ![]() - двухстороннее преобразование
Лапласа функции f.
- двухстороннее преобразование
Лапласа функции f.
Доказательство:
Отметим, что по теореме Фубини можно написать:
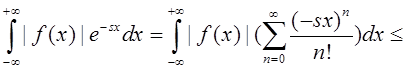
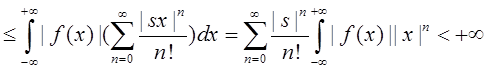 , если
, если ![]() , т.е.
для функции
, т.е.
для функции ![]() определено двухстороннее
преобразование Лапласа.
определено двухстороннее
преобразование Лапласа.
Теперь получаем:
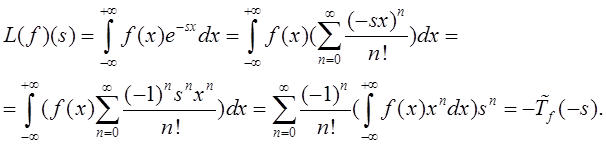
Изменение порядка интегрирования и суммирования законно, т .к.
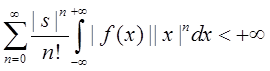 ,
, ![]() .
.
Теорема доказана.
Рассмотрим теперь
отображение ![]() задаваемое преобразованием
Лапласа:
задаваемое преобразованием
Лапласа: ![]()
Теорема 4.8. Отображение ![]() является изоморфизмом векторных
пространств.
является изоморфизмом векторных
пространств.
Доказательство:
а)
инъективность (![]() ):
):
пусть
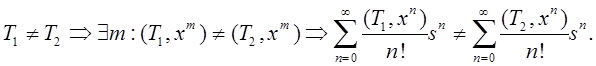
б) сюръективность: пусть
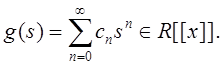
Рассмотрим
![]()
![]()
Теорема доказана.
Рассмотрим
формулу обращения для преобразования Лапласа в пространстве формальных
обобщенных функций ![]() .
.
Теорема 4.9. Пусть ![]() и
и ![]() ,
,
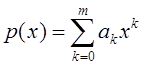 . Тогда произведение
. Тогда произведение ![]() является корректно определенным
элементов из пространства
является корректно определенным
элементов из пространства 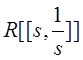 и (T,p)=Res
и (T,p)=Res ![]()
![]()
Доказательство:
Пусть
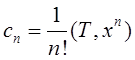 и
и ![]() Тогда
Тогда
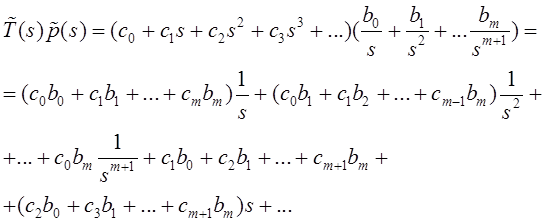
Поэтому  и
и
Res 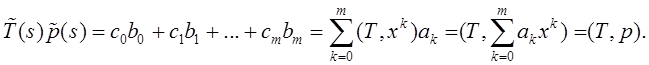
Теорема доказана.
Замечание.Равенство ![]() =Res (
=Res (![]() ) можно
рассматривать как аналог равенства Парсеваля из теории преобразования Фурье.
) можно
рассматривать как аналог равенства Парсеваля из теории преобразования Фурье.
Для преобразования
Лапласа в пространстве ![]() имеет место
аналог теоремы 3.3.
имеет место
аналог теоремы 3.3.
Теорема 4.10. Пусть ![]() . Тогда
. Тогда ![]()
Доказательство:

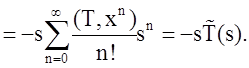
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.