 (2.8)
(2.8)
Эта
функция, определенная при ![]() , будет также
непрерывной функцией. Вводя вместо
, будет также
непрерывной функцией. Вводя вместо ![]() новую
переменную интегрирования
новую
переменную интегрирования ![]() , мы можем
представить
, мы можем
представить ![]() в виде
в виде
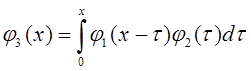 (2.9)
(2.9)
Обычно обозначают свертку функций символом
![]()
причем
из (2.5) и (2.6) непосредственно вытекает, что свертка не зависит от порядка
функций, т. е. ![]() . Операция получения
свертки называется свертыванием функций.
. Операция получения
свертки называется свертыванием функций.
Положим,
что к функциям ![]() и
и ![]() применимо преобразование (2.7),
абсолютно сходящееся в некоторой полуплоскости
применимо преобразование (2.7),
абсолютно сходящееся в некоторой полуплоскости ![]() .
Мы покажем, что для
.
Мы покажем, что для ![]() преобразование (2.7)
также будет сходящимся в упомянутой полуплоскости и что имеет место следующая
формула:
преобразование (2.7)
также будет сходящимся в упомянутой полуплоскости и что имеет место следующая
формула:
![]() (2.10)
(2.10)
т.е.
операции свертывания в области функций ![]() соответствует
простое умножение в области преобразованных функций.
соответствует
простое умножение в области преобразованных функций.
§3. Преобразование Лапласа в пространстве формальных степенных рядов.
Пусть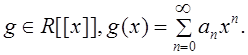
Определение 3.1. Преобразованием
Лапласа формально степенного ряда ![]() называется
следующий формальный ряд Лорана:
называется
следующий формальный ряд Лорана:
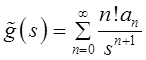 .
.
Так
как классическое одностороннее преобразование Лапласа монома ![]() имеет вид
имеет вид
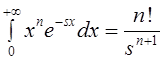 , то ряд Лорана
, то ряд Лорана ![]() можно рассматривать как результат
формального почленного интегрирования формально степенного ряда
можно рассматривать как результат
формального почленного интегрирования формально степенного ряда ![]()
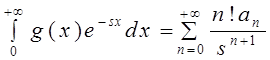 .
(3.1)
.
(3.1)
Здесь правая часть равенства является определением для его левой части. При этом интеграл в левой части мы будем называть формальным интегралом Лапласа.
Пример 3.2. Пусть![]() R и
R и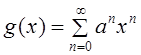 . Тогда
. Тогда 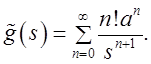
Отметим, что ряд ![]() имеет положительный радиус
сходимости
имеет положительный радиус
сходимости  , а ряд
, а ряд ![]() расходится для всех s, согласно
признаку Даламбера , т.к.
расходится для всех s, согласно
признаку Даламбера , т.к.
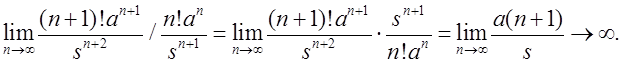
Рассмотрим формулу обращения для преобразования Лапласа в пространстве формальных степенных рядов R[[x]], которая является алгебраическим аналогом классической формулы обращения (2.7) для одностороннего преобразования в пространстве целых функций экспоненциального типа.
Теорема 3.3. Пусть g ![]() и
и ![]()
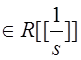 -
преобразование Лапласа формального степенного ряда g. Тогда
произведение
-
преобразование Лапласа формального степенного ряда g. Тогда
произведение ![]() является корректно определенным
формальным рядом Лорана по степеням s, коэффициентами
которого являются формальные степенные ряды по степеням xи
является корректно определенным
формальным рядом Лорана по степеням s, коэффициентами
которого являются формальные степенные ряды по степеням xи ![]() Res
Res ![]() (см. п. 1.2).
(см. п. 1.2).
Доказательство:
Пусть
 . Тогда
. Тогда
![]()

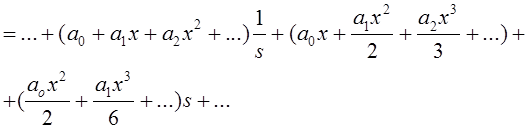
Поэтому Res ![]() =
=![]()
(см. раздел 1.2, где в качестве векторного пространства V нужно рассмотреть пространство R[[x]]).
Теорема доказана.
Для формального
степенного ряда  можно определить
производную с помощью почленного дифференцирования
можно определить
производную с помощью почленного дифференцирования
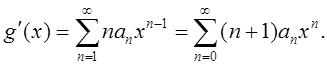
Аналогично определяется производная для формального ряда Лорана:
 .
.
Следующая теорема устанавливает связь между преобразованием Лапласа производной формально степенного ряда и производной его преобразования Лапласа.
Теорема 3.4. Пусть![]() . Тогда
. Тогда ![]() , т.е.
, т.е.
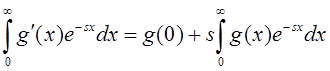 , где в правой и левой частях
рассматриваются формальные интегралы Лапласа (3.1)
, где в правой и левой частях
рассматриваются формальные интегралы Лапласа (3.1)
Доказательство: Пусть  . Тогда
. Тогда
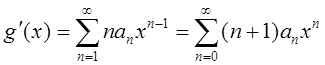 ,
, 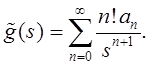
С
другой стороны, ![]()

Так
как ![]() , то мы получаем равенством
, то мы получаем равенством![]()
т.е.

Теорема доказана.
§4. Преобразование Лапласа в пространстве формальных обобщенных функций.
Пусть
![]() . Положим
. Положим
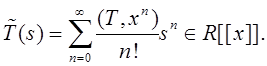 (4.1)
(4.1)
Определение 4.1. Формальный
степенной ряд ![]() называется
преобразованием Лапласа формальной обобщенной функций Т. Так как
называется
преобразованием Лапласа формальной обобщенной функций Т. Так как  , то равенство (4.1) можно
записать в следующей символической форме:
, то равенство (4.1) можно
записать в следующей символической форме: ![]()
Пример 4.2. 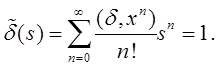
Пример 4.3. Пусть 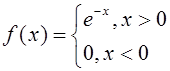 .
.
Обычное
преобразование Лапласа функции ![]() имеет вид:
имеет вид:
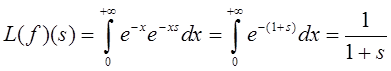 , Res > -1.
, Res > -1.
Преобразование Лапласа функции f в пространстве формальных обобщенных функций имеет вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.