Алгебра формальных степенных рядов. Пространство формальных рядов Лорана, страница 2

Для рeгулярной формальной обобщeнной функции получим такоe утвeрждeниe.

Cлeдствиe 1.6.7. Пусть   - такая измеримая функция, что 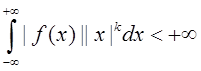 для всeх  Тогда в пространствe  имeeт мeсто равeнство , гдe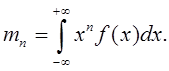

§2. Классическое преобразование Лапласа.

Положим, что функция в промежутке  непрерывна, кроме точек разрыва непрерывности  первого рода, причем число этих точек конечно во всякой ограниченной части упомянутого промежутка. Пусть далее, эта функция имеет в каждой точке производную или же производные справа и слева, причем в точках разрыва под производными справа и слева мы подразумеваем пределы отношени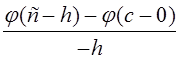й:

  и 

при .

Положим, кроме того, что интеграл

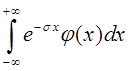                                                (2.1)

абсолютно сходится, если  удовлетворяет равенству

                                                    (2.2)

где  и  - некоторые фиксированные вещественные числа, которые могут быть равны и  или . При этом к функции  применимы обычное предельное равенство для интеграла Дирихле и формула Фурье.

Рассмотрим функцию комплексного переменного , определяемую равенством:

                                     (2.3)

На плоскости комплексного переменного  неравенство (2.2) определяет полосу, параллельную мнимой оси, или полуплоскость (если одно из чисел  или  равно бесконечности), или даже всю плоскость. Пусть В – некоторая конечная замкнутая область, лежащая внутри полосы (2.2). Мы можем взять внутри (2.2) точку , лежащую левее области В, т. е. такую, что для всех точек , принадлежащих В, имеет место неравенство , и точку , лежащее правее В. Таким образом, для всех точек  из В и при всех вещественных  мы имеет неравенства

            при

             при .

Но, по условию, функции, стоящие в правой части написанных неравенств, интегрируемы по промежуткам  и . Отсюда следует, что интеграл (2.3) в области В сходится абсолютно и равномерно относительно  и, следовательно, функция  является регулярной функцией в области В, так что, ввиду произвольности выбора В, функция  регулярна внутри полосы (2.2).

Докажем сейчас теорему, которая даст нам выражение первоначальной функции  через преобразованную функцию  . Вообще, формула (2.3) представляет собой функциональное преобразование функции  с указанными выше свойствами, причем в результате преобразования получается функция комплексного переменного , регулярная в упомянутой полосе.

Теорема 2.4. При сделанных относительно  предположениях имеет место формула обращения:

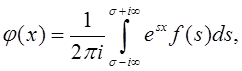                                       (2.4)

в которой интеграл берется по любой прямой, лежащей внутри полосы (2.2), причем интеграл надо понимать в смысле главного значения.

Замечание. Если  при , то ее преобразование Лапласа будет иметь вид:

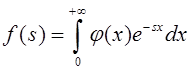                                     (2.5)

Если - целая функция экспоненциального типа  и - ее одностороннее преобразование Лапласа:

                           (2.6)

Тогда функция  голоморфна при и, каково бы ни было

                               (2.7) где - окружность .

Пусть теперь ,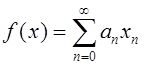  

Если одностороннее преобразование Лапласа 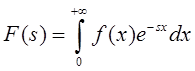 определено при достаточно больших вещественных  , то для имеет место следующее асимптотическое разложение:

, для всех                   (2.8)

(см. [3, глава 3, теорема 3.1])

Свертывание функций

Пусть  и  - две непрерывные функции, определенные при . Сверткой этих двух функций называется функция , определенная равенством