Задание на курсовую работу:
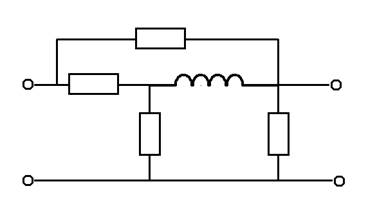
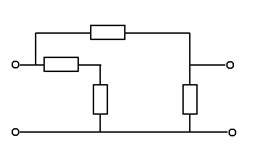
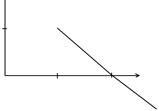
Схема:
|
|
|
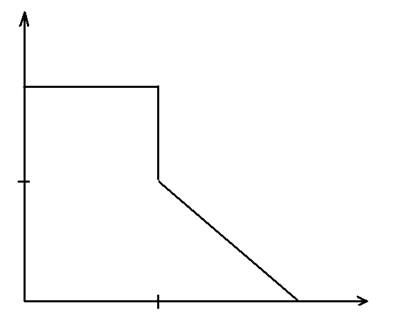
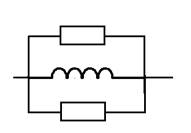
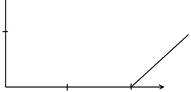
Входной сигнал:
|
|
|
|
I. Вычисление переходной реакции цепи
Переходная реакция цепи вычисляется как реакция цепи на входное воздействие в виде единичной функции 1(t). Численно она равны напряжению на выход цепи и равна:
Состояние цепи по-прошествии бесконечно большого отрезка времени.
Напряжение на выходе цепи будет равно:
I2 = 1/2I1 => U2 = I2*Rэкв
Rэкв =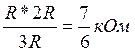 
U2 = I2*Rэкв = 0,856*0,5 = 0,428 В
Cостояние цепи в момент времени t = 0+.
Напряжение на выходе цепи будет равно:
U2 = 1/2U1 = 0.5B
Из выше рассчитанных данных получим величину свободной составляющей:
U2 = 0,428+A*ept => 0.5 = 0.428+A => A=0.072
Рассчитаем P:
т =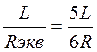
=> P
= -
= -1200
Окончательно имеем: g(t)=0.428+0.072*e-1200t
Рассчитаем импульсную характеристику H(jw) цепи через g(t), логическая цепочка для расчета выглядит следующим образом:
g(t) => h(t) => h(jw)
h(t) = g`(t)+g(0)*6(t) = 0.5*6(t)+0.072*(-1200)e-1200t =>
h(jw) =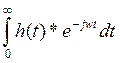 
=0.5-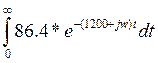
= 0.5- 
= 
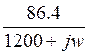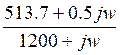
II. Вычисление интеграла Дюамеля:
Весь отрезок времени разбивается на 3 интервала. Границы интервалов приходятся на t0=0 mc, t1=2 mc, t2=4 mc. Значения функции входного сигнала и его производных на каждом интервале в отдельности приведены ниже. Выходное напряжение запишется так:
Первый интервал:
0 ≤ t ≤t1
U(0) = 10 B
U(t) = 10
U’(t) = 0
U2(t) = U(0)*g(t)+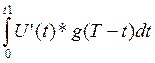
= 4.28+0.72*e-1200t
Второй интервал:
t1 ≤ t ≤t2
U(t1) = -5 B
U(t) = -2500 B/c
U’(t) = 0
U2(t) = U(0)*g(t)+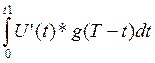+ U(t1)*g(t-t1)+
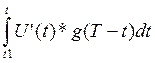= 4.28+0.72*e-1200t
– 2.14 – 0.36* e-1200(t-t1) +2.14 – 1070t+0.15* e-1200t =
4.28+0.51 e-1200t-1070*t
Третий интервал:
t2 ≤ t ≤ ∞
U(t2) = 0 B
U(t) = -2500 B/c
U’(t) = 0
U2(t) = U(0)*g(t)+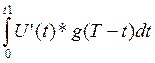+ U(t1)*g(t-t1)+ 
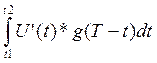+ U(t2)*g(t-t2)+ 
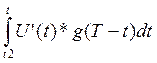= 4.28+0.72*e-1200t – 2.14 – 0.36* e-1200t
+2.12 – 1070t+0.15* e-1200t = 4.28-2.14+0.72*
e-1200t-0.36* e-1200t – 2.14 = 0.36* e-1200t
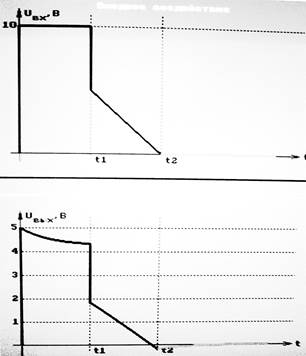
График функции на выходе построен при использовании программы DML.
|
III. Нахождение спектральной плотности входного сигнала.
Для нахождения спектральной плотности входного сигнала функция сигнала U1(t) представляется в виде суммы четырёх «простейших» функций, изображенных ниже.
f1(t) = 0, при
t<0 f1(t) => F2(p)
= 
f1(t) = 10, при t≥0
f2(t) = 0, при
t<0 f2(t) => F2(p)
= - 
e-pt1
f2(t) = -5, при t≥0
f3(t) = 0, при
t<0 f3(t) => F3(p)
= - 
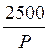e-pt1
f3(t) = -2500*t, при t≥0
f4(t) = 0, при
t<0 f4(t) => F4(p)
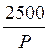= e-pt2
f4(t) = 10, при t≥0
Изображение входного сигнала записывается как сумма «простейших» функций:
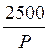F(p) = F1(p)+F2(p)+F3(p)+F4(p) = - e-pt1 - e-pt1 + 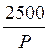e-pt2 = -coswt1
- 
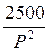coswt1 + 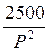coswt2 – j(sinwt1 + 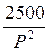sinwt1 - 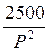sinwt2)
АЧХ спектральной плотности входного сигнала:
U1=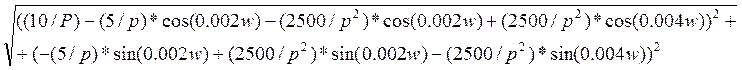
Его фазовая характеристика:
=arctg
= 
|
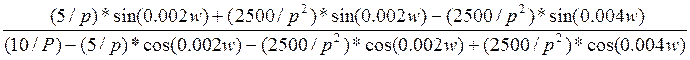
F, кГц |
S1(f) |
Ф1(w) |
H(w) |
ФН(w) |
U2(w) |
Ф2(w) |
|
0.15 |
17.798 |
95.762 |
0.429 |
0.051 |
7.628 |
68.745 |
|
0.3 |
6.794 |
110.22 |
0.429 |
0.103 |
2.912 |
110.32 |
|
0.45 |
2.394 |
111.74 |
0.429 |
0.154 |
1.026 |
111.9 |
|
0.6 |
2.724 |
57.647 |
0.429 |
0.206 |
1.168 |
57.85 |
|
0.75 |
3.194 |
93.957 |
0.429 |
0.257 |
1.369 |
94.214 |
|
0.9 |
1.654 |
117.19 |
0.429 |
0.309 |
0.709 |
117.49 |
|
1.05 |
0.0997 |
61.865 |
0.429 |
0.36 |
0.427 |
62.225 |
|
1.2 |
1.96 |
79.834 |
0.429 |
0.411 |
0.84 |
80.246 |
|
1.35 |
1.42 |
112.47 |
0.429 |
0.463 |
0.609 |
112.93 |
|
1.5 |
0.533 |
90.547 |
0.429 |
0.514 |
0.229 |
91.086 |
|
1.65 |
1.366 |
91.524 |
0.429 |
0.617 |
0.586 |
92.124 |
|
1.8 |
1.277 |
102.9 |
0.429 |
0.668 |
0.535 |
103.5 |
|
1.95 |
0.548 |
115.44 |
0.429 |
0.72 |
0.235 |
116.11 |
|
2.1 |
0.742 |
59.66 |
0.429 |
0.771 |
0.318 |
6038 |
|
2.25 |
1.064 |
91.07 |
0.429 |
0.823 |
0.455 |
91.84 |
|
2.4 |
0.693 |
118.5 |
0.429 |
0.874 |
0.274 |
119.32 |
|
2.55 |
0.409 |
63.247 |
0.429 |
0.925 |
0.175 |
64.121 |
|
2.7 |
0.856 |
78.666 |
0.429 |
0.977 |
0.367 |
79.591 |
|
2.85 |
0.689 |
112.23 |
0.429 |
1.028 |
0.295 |
113.21 |
|
3 |
0.236 |
91.094 |
0.429 |
1.176 |
0.114 |
92.112 |
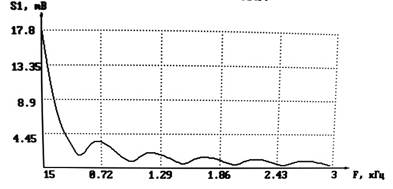
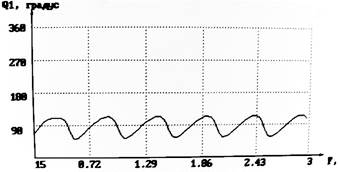
Спектр входного сигнала S1(F) Спектр входного сигнала Q1(F)
График АЧХ цепи График ФЧХ цепи
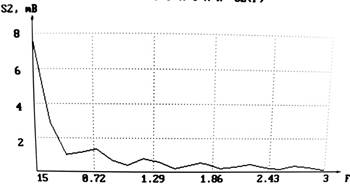
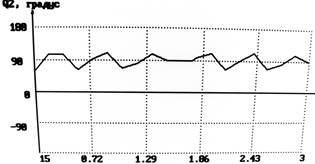
Спектр выходного сигнала S2ц(F) Спектр выходного сигнала Q2(F)
IV. Передаточная функция по напряжению цепи равна:
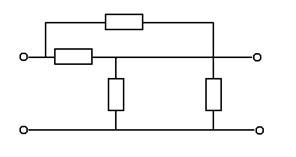
Для упрощения расчетов нам необходимо преобразовать исходную схему цепи методом «звезды», получим:
|
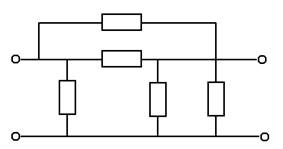
U2 = 
*
;
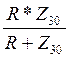Zэкв =
+=
+
= 
;
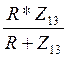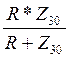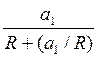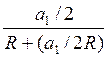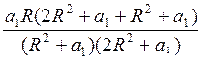H =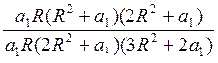 
=
=
;
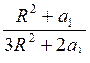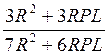Результат расчета совпадает с рассчитанной формулой для H(jw) в пункте I.
V. Дискретизация.
Исходя из данных таблицы необходимо выбрать частоту дискретизации равную 10кГц. Данная частота позволяет наиболее точно представить входной сигнал в виде дискретных отсчетов.
Дискретные значения импульсной характеристики вычисляются по формуле:
H(n)=0.428*6(n)-T*86.4 e-1200*T*n
Дискретные значения функции входного сигнала и импульсной характеристики:
|
t, мс |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
1.6 |
1.7 |
1.8 |
1.9 |
2 |
|
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
U1(t) |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
5 |
|
H(n) |
0.43664 |
-0.0077 |
-0.0068 |
-0.006 |
-0.0053 |
-0.0047 |
-0.0042 |
-0.0037 |
-0.0033 |
-0.0029 |
-0.0026 |
-0.0023 |
-0.0020 |
-0.0018 |
-0.0016 |
-0.0014 |
-0.0013 |
-0.0011 |
-0.001 |
-0.0009 |
-0.0008 |
|
t, мс |
2.1 |
2.2 |
2.3 |
2.4 |
2.5 |
2.6 |
2.7 |
2.8 |
2.9 |
3 |
3.1 |
3.2 |
3.3 |
3.4 |
3.5 |
3.6 |
3.7 |
3.8 |
3.9 |
4.0 |
|
|
N |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
|
|
U1(t) |
4.8 |
4.5 |
4.3 |
4 |
3.8 |
3.5 |
3.3 |
3.0 |
2.8 |
2.5 |
2.3 |
2 |
1.8 |
1.5 |
1.3 |
1 |
0.8 |
0.5 |
0.3 |
0 |
|
|
H(n) |
-0.0007 |
-0.0006 |
-0.0005 |
-0.0005 |
-0.0004 |
-0.0004 |
-0.0003 |
-0.0003 |
-0.0003 |
-0.0002 |
-0.0002 |
-0.0002 |
-0.0002 |
-0.0001 |
-0.0001 |
-0.0001 |
-0.0001 |
-0.0001 |
-0.0001 |
-0.0001 |
Дискретные значения сигнала на выходе цепи вычисляются с помощью формулы дискретной свертки:
U2(t)=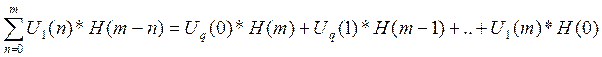 
Дискретный сигнал на выходе цепи:
|
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
t, мс |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
1.6 |
1.7 |
1.8 |
1.9 |
2 |
|
U2(n) |
4.91 |
4.84 |
4.77 |
4.71 |
4.66 |
4.61 |
4.57 |
4.53 |
4.5 |
4.47 |
4,45 |
4.44 |
4.41 |
4.39 |
4.38 |
4.36 |
4.35 |
4.33 |
4.32 |
4.31 |
1.85 |
|
N |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
|
|
t, мс |
2.1 |
2.2 |
2.3 |
2.4 |
2.5 |
2.6 |
2.7 |
2.8 |
2.9 |
3 |
3.1 |
3.2 |
3.3 |
3.4 |
3.5 |
3.6 |
3.7 |
3.8 |
3.9 |
4.0 |
|
|
U2(n) |
1.75 |
1.66 |
1.57 |
1.47 |
1.37 |
1.27 |
1.17 |
1.07 |
1.97 |
0.87 |
0.77 |
0.67 |
0.57 |
0.46 |
0.36 |
0.26 |
0.15 |
0.05 |
-0.06 |
-0.16 |
Спектральная характеристика дискретизированного сигнала U1(t) могут быть вычислены на любой частоте, однако для упрощения расчетов целесообразно ограничиться 4-5 значениями частоты, на которых показательная функция ejwnt легко вычисляема:
U1(0) = T *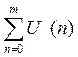
Результат вычисления спектральной плотности дискретизированного сигнала U1(t) по формуле:
U1(jw) = T*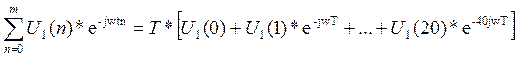
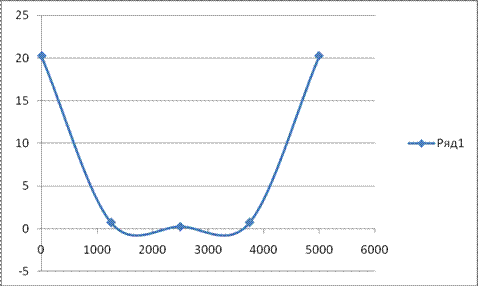
U1(0) = 20.25
U1(1250) = 0.75
U1(2500) = 0.25
U1(3750) = 0.75
U1(5000) = 20.25
Z-преобразование дискретной цепи, дискретные значения которой H(n) приведены в таблице, записывается в виде:
Н(Z) = 0.428-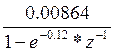
Учитывая, что Z-преобразование входного и выходного дискретных сигналов связаны между собой соотношением Y(Z)=X(Z)*H(Z), можем записать:
Y(Z) =X(Z)*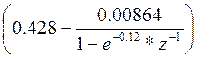 
Путем несложных математических преобразований мы получаем:
Y(Z) = X(Z)*0.42-X(Z)*0.3796*Z-1+Y(Z)*0.887*Z-1
Схема дискретной цепи, реализующее это состояние, имеет вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
= 
= 
= 