Исходные положения о безотказности функционирования организационно-строительных систем, страница 4

40,3;42,3;39,3;36,9;36,0;43,9;42,2;41,8;43,9;29,3.

Математическое ожидание  этих значений Т, вычисленных по формуле (7), составило 39,6 мес., а дисперсия , вычисленная по формуле (8), равна19,1 мес².

По формуле (10) надёжность осуществления строительства за Т_о= Т_к=30,9 месяца

Р () = Ф_о[(-8,7 )/4,37]= Ф_о(-1,99)=2,3%, т.е. сетевая модель является ненадёжна.

Пусть анализ состава производственных ресурсов организаций показывает , что  их можно увеличить на 20% по каждому из ведущих потоков. Тогда Т составит  39,6׃1,2=33 мес.Аналогично приведенному выше получаем

Р () = Ф_о[(-2,1 )/3,64]= Ф_о(-0,58)=28,4%, т.е. сетевая модель является ненадёжна.

Пусть анализ состава производственных ресурсов организаций показывает , что  их можно увеличить на 30% по каждому из ведущих потоков. Тогда Т составит  39,6׃1,3=30,5 мес. Аналогично приведенному выше получаем

Р () = Ф_о[(0,5 )/3,36]= Ф_о(0,12)=54,4%, т.е. сетевая модель является ненадёжна.

Пусть анализ состава производственных ресурсов организаций показывает , что  их можно увеличить на 35% по каждому из ведущих потоков. Тогда Т составит  39,6׃1,35=29,3 мес. Аналогично приведенному выше получаем

Р () = Ф_о[(1,6 )/3,24]= Ф_о(0,49)=68,8%,

Если же привлекаемые производственные мощности можно увеличить на 30%, то надёжность постройки железнодорожного пути за 30,9 мес.,определённая выше способом , составляет 54,4%.

Варьируя количества привлекаемых ресурсов строим графическую зависимость надёжности Р от степени обеспечённости строительства ресурсами S, приведенную на листе 3. Из рисунка 3 следует , что при увеличении количества ресурсов до S=135% надёжность Р становится избыточной.

7.4. Ранжирование потоков для организации контроля за ходом работ

Проверка исполнения утвержденных планов и графиков работ является важнейшим слагаемым обеспечения надежного функционирования строительного производства. Именно надлежащий контроль со стороны органов управления формирует в управляемой системе дисциплинированность, деловитость и оперативность, обеспечивает высокую эффективность работы. Можно принять немало хороших постановлений и приказов по осуществлению заданных программ, где будут четко определены сроки каждого мероприятия и задачи всех исполнителей. Но эти решения так и останутся не воплощенными в жизнь, если не будут осуществляться жесткий контроль и повседневная координация деятельности исполнителей. Но эти решения так и останутся не воплощенными в жизнь, если не будут осуществляться жесткий контроль и повседневная координация деятельности исполнителей. Указанная работа осуществляется систематически с участием всех ступеней иерархической лестницы руководства строительством и является примером реализации халлархической структуры управления .

Организация контроля за ходом выполнения строительного плана, изображаемого в виде сетевой модели, предусматривает распределение потоков работ между ступенями и звеньями (структурными подразделениями или должностными лицами) управления производством. Четкое распределение ответственности по уровням руководства устанавливают на основе использования значений коэффициента напряженности потоков (работ)

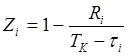                       (48)

где Z_i – коэффициент напряженности I-го потока;

R_i – полный (общий) резерв времени i-го потока на детерминированной сетевой модели;

Т_к – протяженность критического пути детерминированной сетевой модели;

         – суммарная продолжительность функционирования тех потоков на детерминированной модели. Которые входят в состав критического пути и одновременно совпадают с максимальным путем, включающим поток, для которого определяется Z_i.

В общем случае величина Z колеблется в пределах от 0,0 до 1,0 причем значения Z = 1,0 соответствуют потокам и организационным интервалам критического пути. Чем выше коэффициент напряженности, тем более срочный характер имеет рассматриваемая работа и тем выше должен быть уровень руководства (кураторства) на котором осуществляется контроль за ходом реализации данного потока .

Все значения представлены в таблице на листе3.