Исходные положения о безотказности функционирования организационно-строительных систем, страница 3

Тис=15,1;

Пусть для всех специализированных потоков смоделированы n=10 следующих параметров  А_п.1(Т)=1,5; А_п,2(Т)=0,9; А_п.3(Т)=1,7; далее эти значения составили 1,7;1,9;1,5;0,9;0,9;1,1; и последнее значение А_п.10(Т)=1,1. Аналогично этому для других потоковсмоделированы 10 соответствующих значений :

А_ис(Т):1,3;1,7;1,1;1,1;0,9;1,5;1,5;1,5;1,7;0,9.

А_бп(Т):1,3;0,9;1,7;1,1;1,5;1,3;1,7;1,7;1,1;1,1.

А_бщ(Т):1,5;1,7;1,1;1,5;1,1;1,5;1,5;1,1;1,1;1,1.

Тогда вычесления n значений вероятностных продолжительностей четырёх рассматриваемых потоков осуществляются по соответствующим формулам :

Т_п.j= Т_п ,А_і(Т),                (43)

Т_ис.j= Т_ис,А_і(Т),

Т_бщ.J= Т_бщ,А_і(Т),

Т_з.j= ТзА_і(Т).

В результате вычислений получены следующие ряды значений вероятностных продолжительностей :

Т_п.j^в =9;5,4;10,2;10,2;11,4;9,0;5,4;5,4;6,6;6,6.

Т_ис^в =20,9;27,4;17,7;17,1;14,5;24,2;24,2;24,2;27,4;14,5.

Т_бщ^в=6,1;4,2;8,0;5,2;7,1;6,1;8,0;8,0;5,2;5,2.

Т_бщ^в=1,5;1,7;1,1;1,5;1,1;1,5;1,5;1,1;1,1;1,1.

7.3. Обеспечение оптимальной надежности осуществления строительства в заданный срок

Достижение необходимой надежности реализации проекта, т.е. сооружений объекта в срок, установленный инвестором. Может быть обеспечено использованием вероятностных сетевых моделей. Под таким названием чаще всего подразумевают модели с детерминированными сетями и вероятностными оценками работ. По существу это организационно-технологические модели, показывающие взаимосвязь и результаты выполнения комплекса работ, необходимых для достижения одной или нескольких поставленных целей, причем часть параметров моделей или все образующие их элементы являются случайными величинами .

Чтобы определить надежность осуществления строительства железнодорожного участка в срок Т₀  = Т_к, полученный на детерминированном календарном графике или детерминированной сетевой модели, требуется выполнить следующие вычисления. Каждой из величин продолжительности работы потока Т_і на детерминированной сетевой модели последовательно придаются численные значения Т_i,j^в   из рядов вероятностных продолжительностей этой работы, вычисленных в соответствии с указаниями раздела 3. В результате получается п вероятностных сетевых моделей, различающихся численными значениями Т_{i, j}^в   и соответственно значениями продолжительности вероятностных критических путей Т_{i, j}^в   . Усредняя эти продолжительности, находят наиболее ожидаемую продолжительность вероятностных критических путей

Т_к^в = 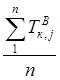                             (44)

Количественно рассеивание значений продолжительности вероятностных критических путей характеризуется дисперсией этой величины

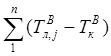=             (45)

На основании центральной предельной теоремы Ляпунова можно допустить, что продолжительности критического пути вероятностных сетевых моделей Т, подчиняются нормальному закону распределения, т.е. закону Гаусса. (Корректность такого допущения возрастает с увеличением числа работ, образующих критический путь). При этом центром симметрии распределения является значение математического ожидания Т, а форма (степень выпуклости) кривой распределения характеризуется средним квадратическим отклонением (Т). Абсолютное значение вероятного отклонения величины Т от заданной (нормативной, детерминированной) продолжительности строительства Т_к  = Т_о обозначается в виде:

.                       (46)

Вероятность Р того, что разность между детерминированным (заданным, ожидаемым с оптимизмом) и вероятностным (реальным, ожидаемым с пессимизмом) значениями продолжительности критического пути не превысит , описывается функцией Лапласа Ф_о:

Р () = Ф_о[(Т_к-Т)/].                 (47)

Значения Ф_о могут быть приняты по данным приложения Б. Очевидно, что надежность осуществления строительства объекта в течение периода времени Т равна 50%.

Сетевые модели считаются надежными при Р 35%, оптимальная надежность составляет 50-60%. Надежность более 65% является избыточной, а менее 25% - недостаточной . Довести надежность осуществления строительства в заданный срок до значений, близких к оптимальному интервалу надежности, можно путем варьирования количества привлекаемых ресурсов. К ним относятся прежде всего производственные мощности строительных организаций: парки строительных и транспортных машин и механизмов, рабочий и инженерно-технический персонал, промышленно-производственный предприятия и вспомогательные хозяйства. В нашем случае общая продолжительность строительства Т_к=30,9 мес.  получается прои расчёте детерминированной сетевой модели , приведенной на листе 3. Применительно к этой модели  получены n=10 значений продолжительностей вероятностных критических путей  Т.Эти значения  составили ряд :