Расчёт коленчатого вала двигателя

1 Расчёт вала

1.1 Общие положения

Для расчёта возьмём простой коленчатый вал, лежащий на двух опорах. Принципиальная схема конструкции показана на рисунке 1.1. Вал состоит из шатунной шейки 1, двух щек 2, двух коренных шеек 3, цапф 4 и 5 и подшипников 8. На вал насажены  шкив 6 и маховик 7. Вал приводится во вращательное движение при помощи шатуна, шарнирно соединённого с поршнем двигателя.

 

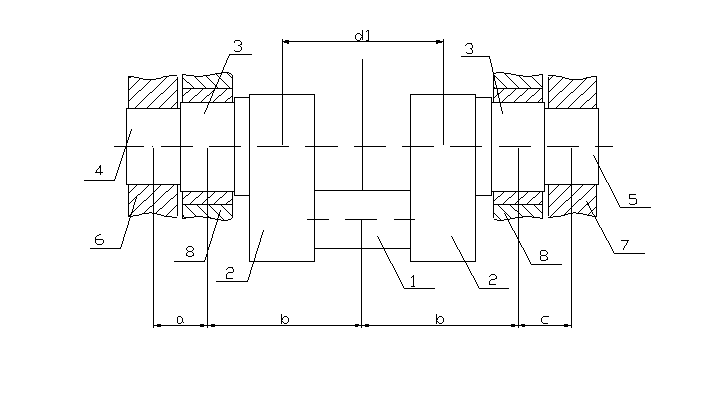
На вал действуют нагрузки:

Р₁  и Р₂ – вес шкива и маховика соответственно;

F – сила, действующая на шатунную шейку со стороны поршня:

Т₁ и  Т₂ – натяжения соответственно сбегающей и набегающей ветвей ременной передачи, посредствам которой крутящий момент передаётся исполнительному механизму.

1.2 Исходные данные

Коленчатый  вал  двигателя  передаёт мощность  N = 400 л.с. при  n = 1600 об / мин через ременную передачу. Вал имеет одно колено с плечом кривошипа r = 170 мм; заданы размеры а = 250мм, b = 350 мм, с = 150мм, d₁ = 200 мм. На  одном конце вала посажен шкив массой m₁ = 520 кг, а на другом – маховик массой m₂  = 1400 кг. Шкив передаёт мощность через ременную передачу под углом α = 40° к горизонту. Натяжение набегающей ветви примем равным двойному натяжению сбегающей ветви. Радиус шкива R = 550 мм. Согласно теоретическим и опытным данным наибольшая нагрузка на вал будет при угле наклона кривошипа к горизонту φ = 40° (расчётное положение вала). Отношение длины шатуна к длине плеча кривошипа l /r = 4,4. Материал вала – сталь 35ХНВ (σ_т=1075  МПа;  σ_-1d=720 МПа).  Коэффициент запаса прочности  к = 1,65.

Вычисление нагрузки, действующие на вал и крутящего момента передаваемого валу через шкив.

Вычислим мощность по формуле:

N = 736 ∙ N (л.с.) = 736 ∙400 = 294400 Вт.

Найдём угловую скорость вращения вала двигателя:

ω  =  πn / 30 = π ∙ 1600 / 30 = 167,47 с^-1,

где n  - частота вращения, об / мин.

Определим массовые силы по формуле Р = mg,,

где g – ускорение свободного падения.

Тогда

Р₁ = m₁ ∙ g =520∙ 9,81 = 5,10 кН;

Р₂ = m₂ ∙ g = 1400 ∙ 9,81 = 13,73 кН.

Линейные размеры вала r = 170 мм = 0,17 м; а = 250 мм = 0,25 м; b = 350 мм = 0,35 м; с = 150 мм = 0,15 м; d₁ =200 мм = 0,2 м;  R = 550 мм = 0,55 м.

1.3 Определение расчётных нагрузок на вал

Определим крутящий момент, возникающий на валу двигателя:

М_к = N / ω = 294400 / 167,47 = 1760 Н∙м.

Натяжение Т₁ сбегающей ветви ременной передачи, считая, что оно вдвое меньше натяжения набегающей ветви, находим по крутящему моменту

Т₁ = М_к / R = 1760/ 0,55 = 3,2 кН.

Следовательно, натяжение набегающей ветви Т₂ = 2Т₁ = 2 ∙ 3,2 = 6,4 кН.

Со стороны шкива под углом α = 40° к горизонту на вал действует изгибающая сила Т = Т₁ + Т₂ = 6,4 + 3,2 = 9,6 кН.

Кроме того, здесь действует вертикальная изгибающая сила от веса шкива Р₁ = 5,1 кН. На противоположном конце вала действует вертикальная изгибающая сила от веса маховика Р₂ = 13,73 кН.

Силу, действующую со стороны шатуна на шатунную шейку вала, разложим на две составляющие – окружную силу F_z, действующую перпендикулярно плоскости кривошипа, и радиальную силу Q_у, действующую в плоскости кривошипа. Индекс показывает, вдоль какой оси координат направлена данная сила. При этом плоскость кривошипа будем рассматривать в положении  под углом φ = 40° к горизонту (расчётное положение). По двум указанным направлениям (у, z) разложим на составляющие силы Т, Р₁,  Р₂.

Окружная сила F_z должна создавать момент, уравновешивающий момент на шкиве, то есть

F_z ∙ r =М_к, кН,

где  r – радиус (плечо) кривошипа, м.

Откуда

F_z = М_к / r = 1,76 / 0,17 = 10,35 Н.

Чтобы оценить радиальную силу Q_у, следует найти угол β. По теореме синусов для углов наклона шатуна кривошипа к горизонту

sin φ / sinβ = 1 / r,

sin β = 1 / 4,4 ∙ sin40° =0,1580 получим  β = 9,13°.

Тогда радиальная сила равна:

Q_у = F_z ctg (φ + β) = 18,35 ctg (40° + 9,13°) = 8,96 кН.

Приведём силы Р₁ и Р₂, приложенные на концах вала к двум системам сил, к силам, действующим в плоскости кривошипа, и к силам, действующим перпендикулярно к плоскости кривошипа.

Сила, действующие в плоскости кривошипа:

Q_1у = Р₁ ∙sinφ – Т ∙cos (α + φ) = 5,10∙sin 40° – 9,6∙cos(40°+40°) = 1,61 кН

Q_2y = Р₂ ∙sinφ = 13,73∙ sin 40° = 8,83 кН.

Найдём реакции опор А_у и В_у, действующие в плоскости кривошипа используя уравнение моментов относительно этих точек:

∑ М_вi =Q_1y(a+2b)+A_y2b-Q_yb+Q_2yc = 0;

А_у = ( 8.96∙0,35 – 1.61(0,25 + 2∙0,35) – 8.83∙0.15) / 2∙0,28 = 0.40 кН;

 ∑М_аi = Q_2y(c+2b) – B_y2b+Q_yb+Q_1ya = 0

В_у = (8.83(0.15+2∙0,35) + 8.96∙0,35 + 1.61∙0,25) / 2∙0,35= 15.78 кН.

Правильность решения уравнений проверим, используя условие равновесия:

∑Y_i = 0;  - Q_y - Q_2y + B_y + A_y + Q_1y = 0;

-1,61-0,40+8,96-15,78+8,83 = 0.

Силы действующие перпендикулярно к плоскости кривошипа ( в плоскости щёк), будут на левом конце вала –

Q_1z = Р₁ ∙cosφ + T∙ sin(α + φ) = 5,10∙ cos40° + 9,6∙ sin(40°+40°) = 13,36 кН;

на правом конце вала –

Q_2z = P₂ ∙cos φ = 13,73 ∙ cos40°= 10,52 кН.

Определим реакции опор А_z  и B_я, действующие перпендикулярно плоскости кривошипа, используя уравнения моментов относительно этих точек:

∑ М_аi  = 0;    0,25∙Q_1z + 0,35∙F_z + 2∙0,35∙B_z – (0,35∙2+с)Q_2z  = 0;

B_z = ( -13,36∙0,25 – 0,35∙10,35 + (0,25+0,7)10,52) / 2∙0,35 = 2,83 кН;

 ∑М_bi = (0,25+0,70)∙Q_1z – 0,70∙A_z – 0,35∙F_z – 0,15Q_2z = 0;

А_z = ((0,25+0,70)13,36 – 0,355∙10,35  + 0,15∙10,52) / 0,70 = 10,70 кН.

Правильность решения уравнений проверим, используя уравнение равновесия:

                                    ∑Z_i = 0;   F_z - B_z +A_z – Q_2z – Q_1z = 0;

13,36-10,7-10,35-2,83+10,52 =0.