Восстановление непрерывной функции в соответствии с формулой Котельникова. Импульсная характеристика фильтра

Обычно число отсчетов ограничено числом  .

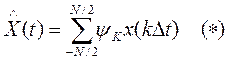 - ошибочное значение, если будет восстанавливаться сигнал по той формуле, то

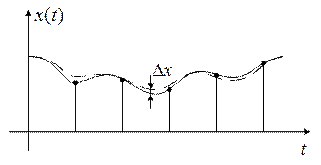
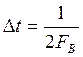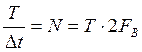,        - количество отсчетов

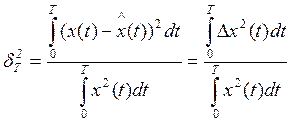 - среднеквадратическая ошибка, она возникает из-за конечного числа отсчетов сигнала. Общая ошибка:

Восстановление непрерывной функции в соответствии с формулой Котельникова может выполняться двумя способами:

1.  Фильтровой

2.  Интерполяционный

Фильтровой заключается в том, что мы подаем отсчеты сигнала на фильтр, импульсная  характеристика которого совпадает с базисной функцией :

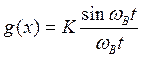
такую импульсную характеристику имеет фильтр у которого частотная характеристика прямоугольная.

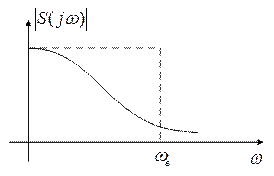
Это физически нереализуемый фильтр, поэтому возникают дополнительные погрешности. При интерполяционном способе восстановления необходимо создать  функций:

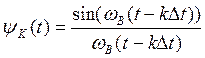, затем умножить их на дискретные отсчеты сигнала и просуммировать. Поэтому на практике формула Котельникова не используется. При дискретизации сигнала важно правильно определить частоту , т. к. спектр дискретного сигнала периодический по частоте.

Важность теоремы Котельникова: она доказывает принципиальную возможность дискретизации причем данная теорема справедлива только для детерминированных сигналов. Для случайных сигналов условия выбора   связаны с интегралом корреляции.

На практике восстановление идет с помощью интерполяционных многочленов (их много) чаще используется интерполяция по формуле Лагранжа:

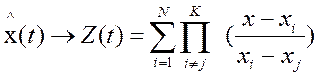
В зависимости от  различают интерполяции разного порядка

ü  “0”- порядка (ступенчатая) ()

РИСУНОК СИГНАЛА

ü  линейная интерполяция ()

РИСУНОК СИГНАЛА

ü  Параболическая

РИСУНОК СИГНАЛА

Эти способы интерполяции ведут к заведомо большой ошибке восстановления, чем по формуле Котельникова, чтобы обеспечить нужную точность нужно . При этом:

ü  Ступенчатый, где 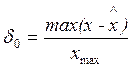- приведенная погрешность восстановления

ü  Линейная  

ü  Параболическая

где .

Методика расчета нужного интервала дискретизации следующая:

1.  Задают величину допустимой погрешности

2.  Определяют по сигналу

3.  По определенному  находят  

4.  Выбирают вид интерполяции

5.  Рассчитывают требуемый интервал дискретизации

Квантование непрерывных сигналов

Суть квантования заключается в том, что бесконечное множество значений сигнала заменяется дискретным конечным множеством заранее установленных значений. В итоге непрерывная шкала мгновенных значений сигнала заменяется дискретной шкалой уровней квантования.

Шаг кантования 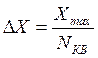  , где - максимальное значение сигнала

 - число уровней квантования

Уровни квантования могут идти с постоянным или с переменным шагом, изменяющимся по некоторому правилу, учитывающем статистику сигнала. Чаще используют равномерное квантование.

РИСУНОК СИГНАЛА

Способы квантования:

1.  Заменяем значение квантуемой величины ближайшим нижним значением сетки квантования

2.  Заменяем ближайшим верхним

3.  Заменяем ближайшим верхним или нижним (округление)

Рассмотрим правило округления:

РИСУНОК СИГНАЛА

Возникает ошибка  причем . Ошибка квантования – шум квантования, его характеристики могут быть различными, но его влияние всегда оценивают мощностью

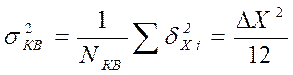
РИСУНОК СИГНАЛА

Запишем отношение сигнал шум квантования:

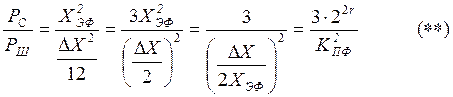, где

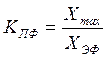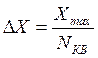- пикфактор сигнала,   - шаг квантования, - число уровней квантования, а r- число разрядов квантователя.

Если сигнал равномерно распределен, то  , а 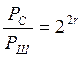. Чаще всего отношение С/Ш выражают в децибелах:

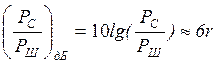
Современные АЦП имеют число разрядов больше 10 – С/Ш больше 60 дБ.  зависит как от числа уровней квантования, так и от самого сигнала.

Преобразование дискретного сигнала в цифровую форму.

Данная процедура заключается в замене мгновенного значения сигнала цифровым представлением выбранного типа квантования. Важно правильно выбрать основание системы счисления. Пусть для представления квантованного значения используется система счисления с основанием  и числом разрядов , тогда число возможных элементов кода равно их произведению:

.

Нужно выбрать ту систему счисления где U минимально.

Параметры сигнала:

, отсюда 

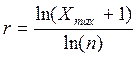 получаем

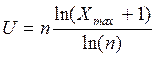
Дифференцируем полученное выражение по n и приравниваем полученное выражение к нулю:

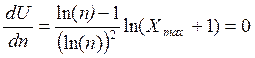
Таблица для различных оснований систем счисления:

Предварительная обработка оцифрованных данных.

Наиболее типичные преобразования:

1.  Изменение формата обрабатываемых данных. АЦП выдает данные в одном формате, а процессору нужен другой. Для согласования надо предусматривать составление соответствующих программ для этих преобразований.

2.  Преобразование данных в реальные физические величины. Одновременно с преобразованием полученных результатов идет преобразование калибровочного сигнала, создается эталон физической величины. В этом случае для преобразования в физические величины определяется соотношение между цифровым представлением отсчетов и эталонным сигналом (калибровка аппаратуры). Эта операция нужна не всегда (иногда нет оценки параметров). Вычисления могут идти в безразмерных величинах, но это должно быть учтено в программе, все расчеты в безразмерной форме.

3.  Улучшение данных. Нужно обнаружить и исключить паразитные выбросы, смещение нулевого уровня, тренд и т.д.

РИСУНОК СИГНАЛА

4.  Выделение полезных составляющих на фоне мешающих

РИСУНОК СИГНАЛА