Структурная схема системы электросвязи. Реализация стационарного гауссовского случайного процесса

аддитивной гауссовой помехи определяется выражением:

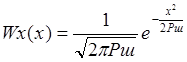
ФПВ огибающей помехи определяется по закону Рэлея: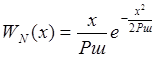       

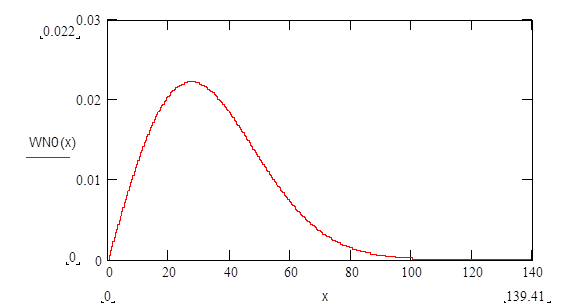ФПВ суммы сигнала и помехи: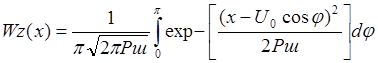       

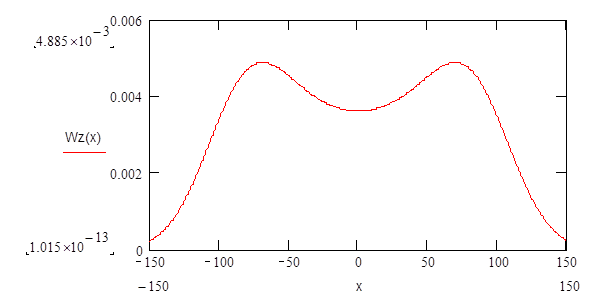ФПВ огибающей суммы определяется распределением Райса:

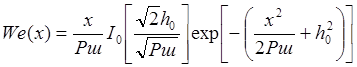, где Io(x) – модифицированная функция Бесселя нулевого порядка от мнимого аргумента.

Задание 9.

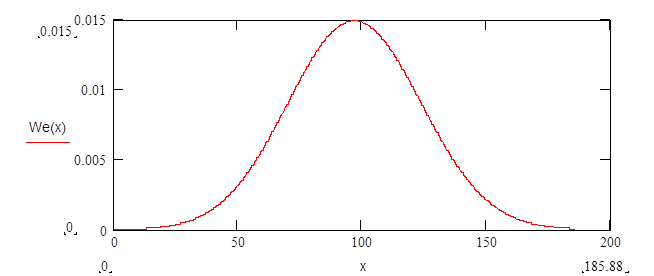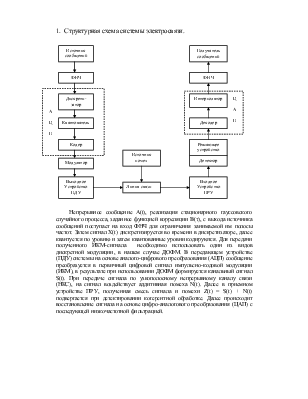
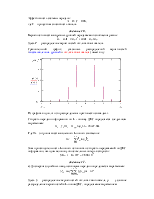
Cхема приемника имеет вид:

Смесь сигнала и помехи поступает на полосовой фильтр, настроенный соответственно на частоту fo с полосой пропускания равной ширине спектра сигнала ДОФМ. Затем происходит детектирование сигнала в фазовом детекторе и с выхода которого сигнал поступает на решающее устройство. После него продетектированная посылка (0 или 1) сравнивается с предыдущей, задержанной с помощью линии задержки, на основании чего делается вывод о том, какой символ, 0 или 1, передавался.

Под действием помех в канале связи РУ может выносить неправильные решения, т.е. могут возникать ошибки первого и второго рода, т.е. p(0|1) и p(1|0). Помехоустойчивость системы характеризуется средней вероятностью ошибки:

Pош_ср = P(0)P(1|0) + P(1)P(0|1) = Pош , при равновероятных символах и ошибках первого и второго рода.

При когерентном приеме для системы с ДОФМ имеем:

6,593×10^-4

Энтропия ошибочных решений:

H_ош = -P_ош log ₂ P_ош - (1-P_ош) log ₂ (1-P_ош))= 7.91×10^-3

Скорость передачи информации по дискретному каналу связи определяют как взаимное количество информации, передаваемой по ДКС, в единицу времени:

R = log ₂ L(1-H_ош)f_д = 26125.5

Эффективность системы передачи:

Э = R / C = 0.06 , где C – пропускная способность канала.

Задание 10.

Вероятности восстановленных уровней передаваемого сообщения равны:

Здесь P_m – распределение вероятностей отклика квантователя.

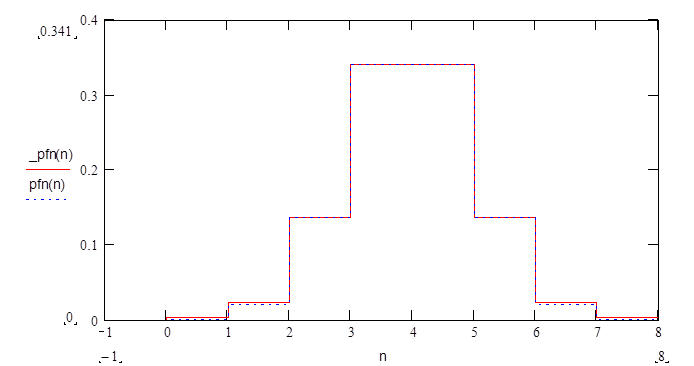
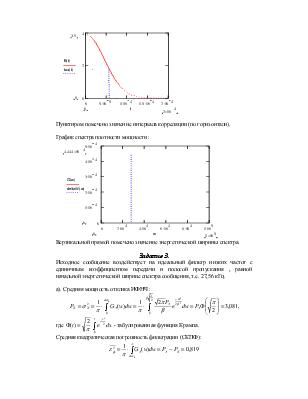
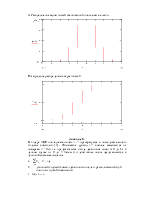
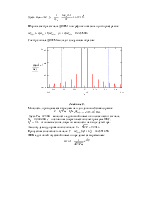
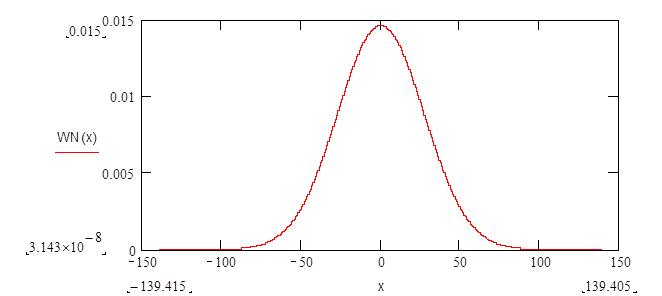
Сравнительный график, указанных распределений вероятностей (восстановленных уровней и отклика квантователя) имеет вид:

Из графика видно, что эти распределения практически совпадают.

Скорость передачи информации по L - ичному ДКС определяется следующим выражением:

= 18327.044

Где Hx – энтропия восстановленного L-ичного сообщения:

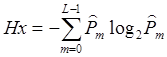
Зная производительность L-ичного источника и скорость передаваемой по ДКС информации, находим величину относительных потерь в скорости:

dR = 1 – R_L / H’ = 7.868×10^-3

Задание 11.

а). Дисперсия случайных импульсов шума передачи определяется выражением:

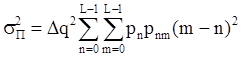
Здесь p_n – распределение вероятностей отклика квантователя, p_nm – условное распределение вероятностей в L-ичном ДКС, определяемое выражением:

, где

d_nm – кодовое расстояние между n-й и m-й кодовыми комбинациями.

Вычисления дают результат: s_п² = 0,059.

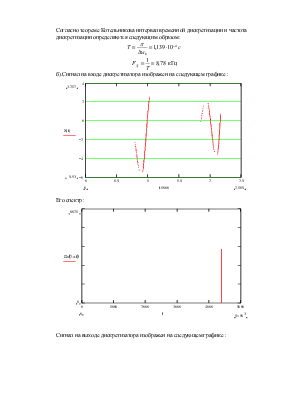
Спектр плотности мощности шума передачи равен:

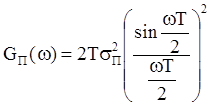
При условии, что ФНЧ на выходе ЦАП обладает полосой пропускания Dw₀, Средняя квадратическая погрешность шума передачи (СКПП) находится следующим образом:

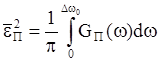
Вычисления дают результат:  = 0,066.

Суммарная начальная СКП восстановления непрерывного сообщения (ССКП)

определяется выражением:

, где

 - СКП фильтрации (см. задание 3),

 - СКП квантования,

 - СКП передачи.

Вычисления дают результат:  = 1,142 Вт.

Относительная СКП (ОСКП) определяется выражением:

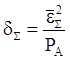
Вычисления дают результат: d_S = 0,293.

б).Сигнал на выходе декодера

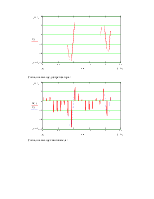
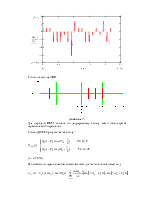
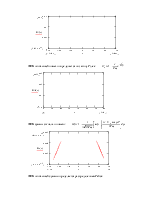
Будем, считать, что сообщение, переданное по каналу связи безошибочно принято приёмником и декодировано, т.е. сигнал на выходе квантователя совпадает с сигналом на выходе декодера.

Сигнал на выходе интерполятора ЦАП

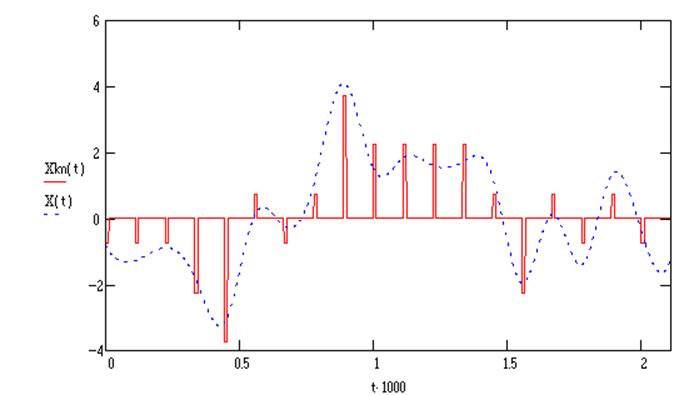
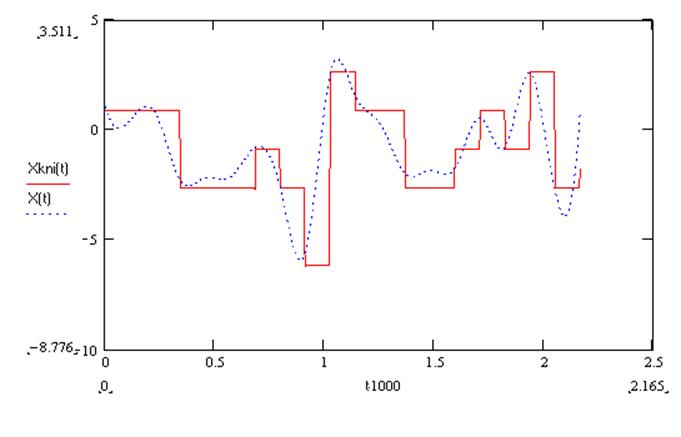
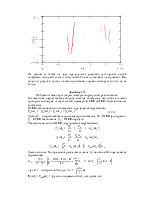
Качественный вид сигнала на выходе системы электросвязи представлен