можно выполнить не только с помощью коррелятора, но и с помощью согласованного фильтра. Согласованный фильтр обеспечивает на выходе наибольшее отношение сигнал/шум при приеме импульсного сигнала на фоне белого шума среди всех линейных фильтров. Фильтр называется согласованным, т.к. его характеристики согласованы с сигналом. Комплексный коэффициент передачи согласованного фильтра:
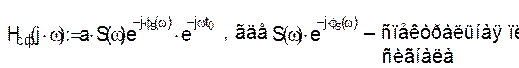
t0 ³ Tc . Импульсная характеристика СФ: g(t) = aS(t0-t).
Отношение сигнал/шум на выходе СФ:
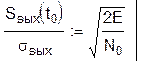
Сигнал на выходе СФ по форме совпадает с корреляционной функцией выходного сигнала Sвых(t) = aK(t-t0)
Корреляционная функция шума на выходе совпадает с корреляционной функцией входного сигнала.
Фильтр, согласованный с одиночным прямоугольным видеоимпульсом:
ìUm, 0 £ t £ tu
S(t) = í
î 0, t<0, t> tu
Спектральная плотность импульса
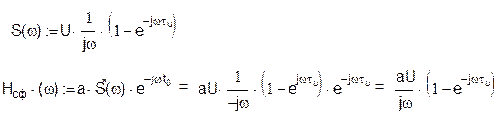
По этой формуле строится схема:

Точная реализация такого устройства невозможна, т.к. нельзя точно проинтегрировать и без искажений задержать сигнал. Поэтому делают реальные фильтры с близкими характеристиками, которые называются квазиоптимальными. Например интегрирующая RC цепь с подобранной полосой пропускания обеспечивает отношение сигнал/шум:
![]()
Специально подобранные фильтры, в которых максимизация отношения сигнал/шум достигнута подбором ширины полосы пропускания, называются согласованными с сигналами по полосе. Но это возможно только для простых сигналов.
При приеме дискретных сообщений количество демодуляторов оценивается безусловной вероятностью правильного приема, или вероятностью ошибки. Схема оптимального демодулятора имеет вид:

В моменты окончания тактов Т, сравниваются напряжения на входах РУ. Эти напряжения являются случайными величинами. Ошибка в приеме символа произойдет, если при передаче 1, например, будет Uру0>Uру1. Для определения вероятности этого события необходимы плотности вероятностей Uру0 и Uру1. Перепишем соотношение:
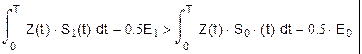
в виде:
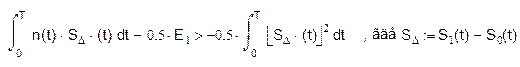

Величина x распределена нормально с мат.ожиданием :

Дисперсия:
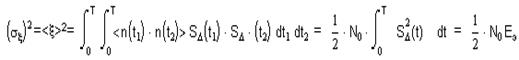
Ошибка произойдет, если будет x< 0.5Eэ .
Вероятность ошибки:
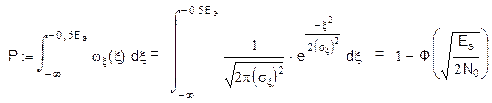
где Ф(z) – интеграл вероятности. При заданной интенсивности помехи, вероятность ошибки зависит от эквивалентной энергии сигналов:

Для сигналов с АМ: Еэ=Е
ЧМ: Еэ=2Е
АМ: Еэ=4Е.
С учетом этого вероятность ошибки для ЧМ:
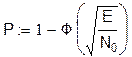
Для ФМ с противоположными сигналами:

Из сопоставления формул для вероятностей ошибок видно, что система с ЧМ дает энергетический выигрыш по максимальной мощности в 2 раза, с ФМ – в 4 раза по сравнению с АМ.
Количество информации в сообщении а определяется по формуле:
 Основание
логарифма : 2
Основание
логарифма : 2
Количество информации в сообщении тем больше, чем оно менее вероятно. Для характеристики всего ансамбля сообщений используется среднее количество информации Н(А):
![]()
Среднее количество информации Н(А) называется энтропией. Если вероятность одного сообщения равна 1, а остальных 0, то Н(А) = 0. Если ансамбль содержит К сообщений, то Н(А) £ log K. Для двоичного источника зависимость энтропии от Р(А) имеет вид:

Энтропия источника зависимых сообщений всегда меньше энтропии источника независимых сообщений. Если объем алфавита К = 32 и буквы выбираются независимо, то Н(А) = log 32 = 5 (бит) на букву. Если буквы составляют связанный русский текст, то они не равновероятны и независимы. Энтропия в этом случае равна Н(А) = 1,5 (бит). Величина:
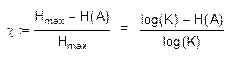
Называется избыточностью источника сообщений с объемом алфавита К. Избыточность показывает, какая доля максимальной энтропии не используется источником. Производительность источника Н`(A) > H(A)/T суммарная энтропия сообщений, переданная за единицу времени.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.