Теория электрической связи. Спектральный анализ периодических и непереодических сигналов. Преобразование частоты радиосигналов

МИНИСТРЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

РЯЗАНСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРИТЕТ

1110

Учебное пособие

по курсу:

Теория электрической связи.

Рязань 2006

Настоящее пособие является продолжением серии изданий для подготовки студентов специальности 2012 «Средства связи с подвижными объектами» к сдаче государственного экзамена. Включает себя основные теоретические сведения по предмету: «Теория электрической связи».

3. ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ.. 4

3.1. Спектральный анализ периодических сигналов. Сигналы с АМ, БМ. 4

3.2.  Спектральный анализ непериодических  сигналов. Прямоугольный видео и радиоимпульсы. 6

3.3. Преобразование спектров сигналов в нелинейных устройствах. Комбинационные  частоты. 9

3.4. Дискретное представление непрерывных сигналов. 11

3.5. Преобразование частоты радиосигналов. 12

3.6. Амплитудный детектор радиосигналов. 14

3.7. Амплитудная модуляция ВЧ колебаний. 16

3.8. Критерии качества и правили приема дискретных сообщений. 17

3.9. Когерентный прием сигналов. 19

3.10. Согласованные и квазиоптимальные фильтры. 20

3.11. Вероятность ошибочного приема точно известных сигналов. 22

3.12. Количество информации, энтропия, избыточность источника сообщений. 24

3. ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ

3.1. Спектральный анализ периодических сигналов. Сигналы с АМ, БМ.

Спектральное представление  периодического сигнала  s(t) находится разложением сигнала в ряд Фурье.

Тригонометрическая форма ряда Фурье:

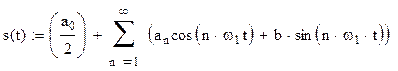
, где      – основная частота периодического сигнала;

Т – период сигнала;

,

.

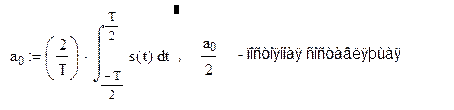
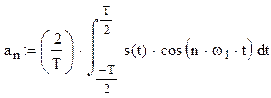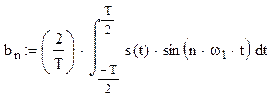n-я гармоника сигнала:

где 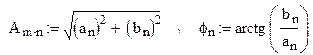 . С учетом этого,

.

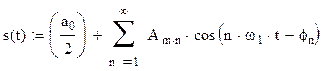Сигнал с амплитудной модуляцией , при модулирующем сигнале ,

, где

А₀ – уровень немодулированной несущей;

М – коэффициент модуляции;

W - модулирующая частота;

g - фаза огибающей;

w₀ - несущая частота;

f₀ - фаза несущего колебания.

Временная диаграмма

Спектральные диаграммы:

Амплитудная

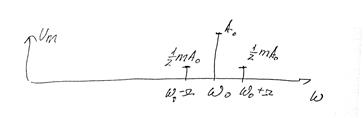
Фазовая

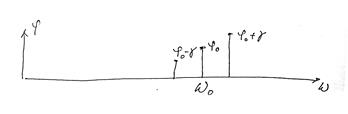
Спектр периодического сигнала – линейчатый.

Сигнал с балансной амплитудной модуляцией.

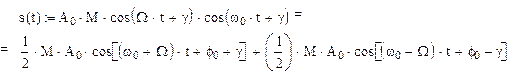
Сигнал с БМ не содержит несущего колебания. БМ энергетически более выгодна.

Спектр:

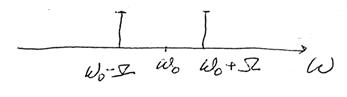
Временная диаграмма:

Огибающая не совпадает по форме с первичным сигналом.

3.2.  Спектральный анализ непериодических  сигналов. Прямоугольный видео и радиоимпульсы.

Спектральным представлением непериодического сигнала s(t)  является его спектральная плотность. Спектральная плотность и сигнал связаны прямым и обратным преобразованиями Фурье:

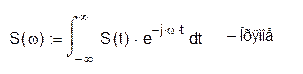
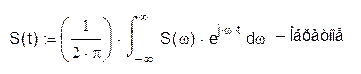
Распишем :

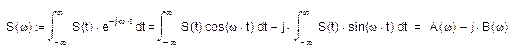
Модуль

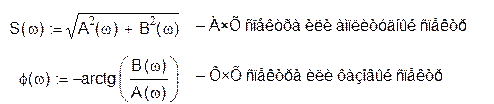
Прямоугольный импульс:

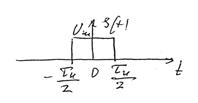
Спектральная плотность:

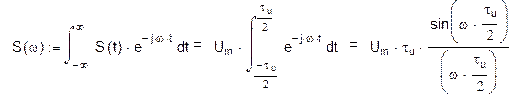
Спектральные диаграммы

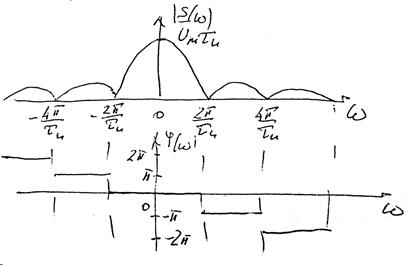
Спектр периодического сигнала – сплошной. Ширина спектра – по первому нулю огибающей.

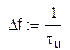
Радиоимпульс:

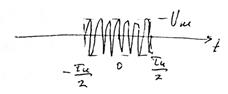
Спектральная плотность:

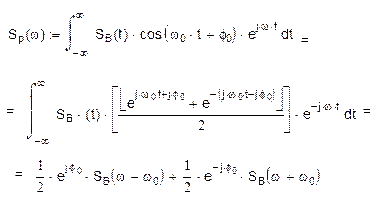
Спектр радиоимпульса соответствует  спектру видеоимпульса, перенесенному в окрестности центральных частот ±w₀.

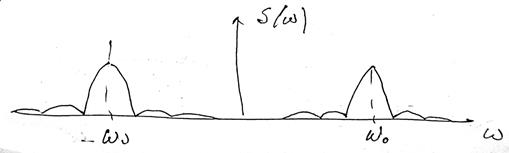
Значение максимумов уменьшилось вдвое, ширина спектра увеличилась в 2 раза.

3.3. Преобразование спектров сигналов в нелинейных устройствах. Комбинационные  частоты.

В отклике нелинейного устройства на входные воздействия может быть достаточно много спектральных составляющих. Одни являются полезными, другие вызывают искажения. Полезные составляющие спектра выделяют для дальнейшего использования,  мешающие – подавляют.

Рассмотрим  преобразование спектра сигнала  при бигармоническом воздействии на нелинейный элемент.

Бигармоническое напряжение:

Считаем характеристику  НЭ полиномиальной,

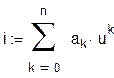
Положим n=3, подставим U(t) и представим ток НЭ в виде суммы гармоник с различными частотами:

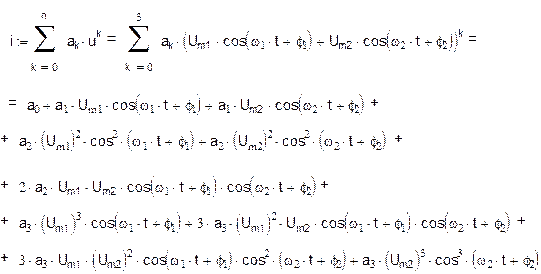
из соотношения видно, что ток содержит три группы составляющих:

- гармоники с частотой k₁w₁ и начальными фазами k₁f₁, k₁=1, 2,…, n;

- гармоники с частотой k₂w₂ и начальными фазами k₂f₂, k₂=1, 2,…, n;

- комбинационные составляющие с частотами k₁w₁± k₂w₂ и начальными фазами k₁f₁ ± k₂f₂ , где |k₁| + |k₂| = 2, 3, … , k₁ и k₂ – отличные от нуля целые числа любого знака.

Комбинационные частоты возникают в нелинейных цепях только при одновременном воздействии двух или большего числа гармонических колебаний.

В данном случае комбинационные частоты  w₁± w₂, 2 w₁± w₂, w₁±2 w₂.

Спектр тока для рассматриваемого случая:

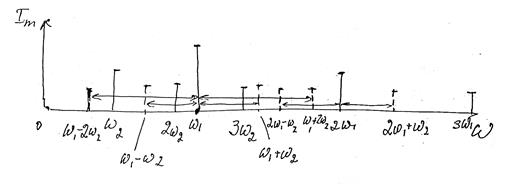
Комбинационные частоты используются при преобразовании частоты, модуляции, синхронном детектировании.

3.4. Дискретное представление непрерывных сигналов.

Дискретное представление непрерывных сигналов широко используется в технике связи. С помощью дискретного представления решаются две основные задачи: многоканальная передача сообщений и цифровая обработка непрерывных сигналов.

Под дискретизацией сигнала S(t) понимается представление непрерывного сигнала с помощью совокупности отсчетов в дискретные моменты времени nDt или nТ.

Интервал между отсчетами выбирается исходя из ширины спектра сигнала. Если S(w) – спектральная плотность исходного непрерывного сигнала, то спектральная плотность S_T(w) дискретизированного сигнала.

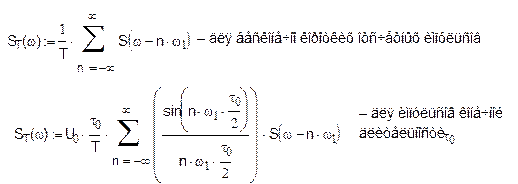
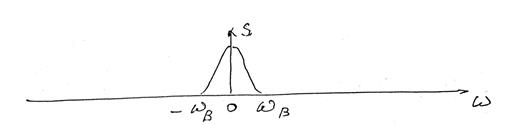
Спектральные диаграммы:

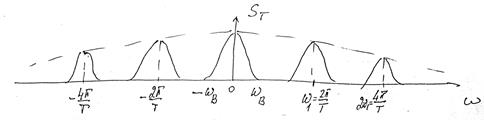
(Огибающая обусловлена конечной длительностью отсчетных импульсов.)

Если

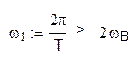, то отдельные спектры не перекрываются, и их можно разделить с помощью фильтров. При этом сигнал может быть восстановлен достаточно точно.

Исходя из соотношения w₁ > 2w_B можно определить требования к интервалу дискретизации сигнала

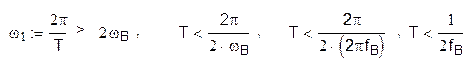
Если интервал между отсчетами взять больше 1/2f_B , то спектры перекроются.

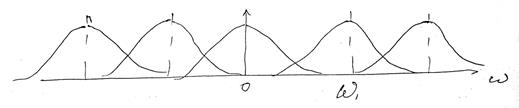
Из-за перекрытия спектров восстановление сигнала по отсчетам станет невозможным.

При широком спектре исходного дискретизируемого сигнала перед дискретизацией его спектр ограничивают частотой f_B.