Теория электрической связи. Спектральный анализ периодических и непереодических сигналов. Преобразование частоты радиосигналов, страница 3

Для получения неискаженной модуляции рабочую точку выбирают в середине линейного участка. Статическая модуляционная характеристика рассчитывается по статической характеристике транзистора или снимается экспериментально. Полоса пропускания контура модулятора выбирается из условия Df > 2F_в.

3.8. Критерии качества и правили приема дискретных сообщений.

При приеме дискретных сообщений на вход демодулятора на тактовом интервале 0 – Т поступает элемент сигнала Z(t) = S_i(t) + n(t), где S_i(t) – сигнал, соответствующий символу b_i , n(t) – шум. Демодулятор на основе принятого колебания Z(t) должен принять наилучшее по заданному критерию решение о передаваемом символе b_i . В технике связи преимущественно применяют критерии максимального правдоподобия и идеального наблюдателя (критерий Котельникова). По критерию идеального наблюдателя наилучшим является демодулятор, обеспечивающий наибольшую безусловную вероятность правильного приема символа. Вероятность того, что принятое решение правильно, равна условной вероятности Р(b_i|Z) того, что действительно передавался символ b_i , при условии прихода реализации Z(t). Эту вероятность называют апостериорной вероятностью символа b_i . Критерий идеального наблюдателя обеспечивается решающей схемой, реализующей правило максимума апостериорной вероятности. По критерию идеального наблюдателя принимается такое решение b_i , для которого апостериорная вероятность

Р(b_i|Z) максимальна. Р(b_i|Z) > Р(b_j|Z) , j=0, 1, … , m-1, i ¹ j.

Для двоичной системы: Р(1|Z) > Р(0|Z). Апостериорная вероятность вычисляется по формуле обратной вероятности или формуле Байеса:

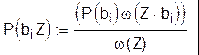
где P(b_i) – априорная вероятность передачи символа b_i . С учетом формулы Байеса правило решения принимает вид:

P(b_i)w(Z | b_i) > P(b_j)w(Z | b_j), j=0, 1,…, m-1, i ¹ j.

Плотность вероятности называется функцией правдоподобия. Правило максимума апостериорной вероятности можно записать иначе:

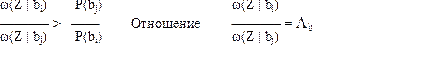
Называется отношение правдоподобия. Если символы передаются равновероятно, то

, то правило принятия решения принимает вид L_ij >1.

Это правило реализует критерий максимума отношения правдоподобия. Отношение правдоподобия может быть составлено по отношению к нулевой гипотезе. Z(t) = n(t)

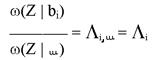
Тогда правило принятия решения для двоичной системы может быть записано в виде L₁ > L₀. Существуют и другие критерии качества приема сигналов.

3.9. Когерентный прием сигналов.

Когерентный прием используется при приеме точно известных чигналов на фоне белого шума. На входе демодулятора действует колебание:

Z(t) = S_i(t) + n(t),  0 £ t £ T .

По критерию максимального правдоподобия необходимо найти отношение правдоподобия для всех m возможных сигналов относительно нулевой гипотезы S(t) = 0, Z(t) = n(t).

Для квазибелого шума с полосой F функция правдоподобия для нулевой гипотезы имеет вид:

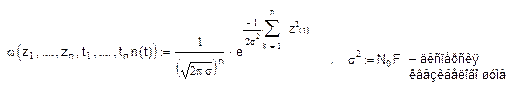
Функция правдоподобия для символа b_i:

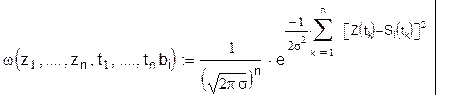
Отношение правдоподобия для сигнала S_i:

После перехода к белому шуму правило максимального правдоподобия можно записать в виде:

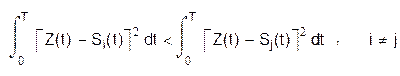
или для двоичной системы:

Последние выражения определяют операции, которые должен совершить оптимальный приемник над выходным колебанием Z(t). Устройство, вычисляющее скалярное произведение

 

называется активным фильтром, или коррелятором, поэтому такой приемник называется корреляционным.

Структурная схема корреляционного приемника двоичных сигналов:

В моменты времени, кратные Т, ключ замыкается и РУ определяет номер ветви с максимальным сигналом.

3.10. Согласованные и квазиоптимальные фильтры.

Основную операцию оптимального приема