Определения, формы представления графов. Матричное представление графов. Матрица инциденций неориентированного графа, страница 4

Пусть граф G (Х, А) с n  вершинами имеет гамильтонов цикл и получено его изображение, в котором ребра гамильтонова цикла не пересекаются, как на рис. 4.2 б. Тогда во внутренней и внешней областях по отношению к циклу Гамильтона можно провести без пересечений не более (n-3) ребер[1]. Cледовательно,  максимальное число ребер (некратных) у плоского графа :

m_max = n + (n - 3) + (n - 3) = 3(n - 2).

Кроме того, что если число некратных ребер графа m £ n + 2 то такой граф заведомо плоский [1]

Числом планарности графа называется минимальное число ребер, которое необходимо удалить из графа для получения его плоского изображения. Например, для графа на рис. 4.3 число планарности равно единице, т.к. для получения его плоского изображения необходимо удалить, как это видно из рисунка, одно ребро (х₁, х₄).

Минимальное число плоских суграфов, которое можно выделить в графе, называют толщиной графа. Толщина графа определяет минимальное число плоскостей (слоев), на котором может быть размещен граф без пересечения ребер в каждом слое.

Упражнения

4.1. Будут ли одинаковыми матрицы смежности и индиденций для графов G, G¢ и G¢¢ на рис.4.2?

4.2. Чему равно число ребер в полном графе?

4.3. Является ли плоским граф, который может быть изображен проволочной моделью куба?

4.4. Привести примеры графов с шестью вершинами, не являющихся плоскими.

4.5. Показать, чему равно число планарности полного графа с пятью вершинами.

4.6. Являются ли графы G₁и G₂ на рис .4.4 изоморфными?

4.7. Определить число планарности и толщину графов G₁ и G₂  на рис. 4.4.

4.8. Определить толщину графа с мощностью множества вершин от 1 до 10, т.е. çхç=1 ¸ 10.

5. ОПЕРАЦИИ НАД ГРАФАМИ

5.1. Объединения графов

Объединение G(Х, Г) графов G₁(Х₁ ,Г₁) и G₂ (Х₂, Г₂) записываемое как  G(Х, Г)=G₁(Х₁, Г₁) È G₂(Х₂, Г₂), осуществляется по следующим правилам: 1) вершинами графа G(Х, Г) является объединение множеств вершин исходных графов: Х = Х₁ È Х₂; 2) отображение для каждой вер-шины графа G получают путем объединения отбражений этой вершины для исходных графов (" х_iÎХ) [Г(х_i) = Г₁(х_i) È Г₂(х_i)].

Рассмотрим пример. Пусть заданы графы G₁ и G₂, аналитические, геометрические и матричные представления которых изображены на рис. 5.1 и 5.2, соответственно.

Х₁={х₁, х₂, х₃, х₄}, Г₁(x₁)={х₁, х₂, х₃},

Г₁(x₂)={х₃},

Г₁(x₃)={х₁},

Г₁(x₄)={х₂,х₃}.

Х₂={х₁,х₃,х₅},

Г₂(Х₁)={х₁,х₃},

Г₂(Х₃)={х₃,х₅},

Г₂(Х₃)={х₁},

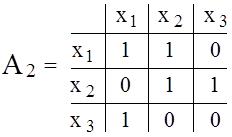
Тогда  соответствующие представления графа G=G₁ÈG₂ имеют вид, изображенный на рис. 5.3.

Х = Х₁ È Х₂ = {х₁, х₂, х₃, х₄, х₅}

Г(х₁) = Г₁(х₁) È Г₂(х₁)={х₁, х₂, х₃},

Г(х₂) = {х₃},

Г(х₃) = Г₁₍х₃) È Г₂₍х₃)  = {х₁, х₃, х₅},

Г(х₄) = {х₂, х₃},

Г(х₅) = {х₁}

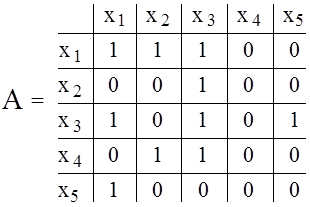
При матричном представлении порядок исходных матриц можно сделать n x n, где n – мощность множества Х, путем добавления нулевых строк и столбцов, соответствующих тем вершинам, которые есть в объединении графов, но отсутствуют в исходных графах. Тогда любой элемент матрицы А оказывается дизъюнкцией соответствующих элементов в полученных таким способом матрицах.

В рассмотренном примере порядок исходных матриц следует сделать 5 х 5 путем добавления в матрицу А₁ нулевых строки и столбца, соответствующих вершине х₅, и путем добавления  в матрицу А₂ нулевых строк и столбцов, соответствующих вершинам х₂ и х₄ так, как это показано на рис. 5.4.

Операцию объединения можно распространить и на большее число графов. При этом объединяются как множества вершин, так и множества исходных ребер.

    

Рис. 5.4

5.2. Пересечение графов.

Пересечение G(Х, Г) графов G₁ (Х₁, Г₁) и G₂ (Х₂, Г₂), записываемое как

G(X, Г) = G₁ (X₁, Г₁ ) n G₂ (X₂, Г₂), осуществляется по следующим правилам: 1) вершинами графа G является пересечение множеств вершин исходных графов: Х = Х₁ ? Х₂ ; 2) отображение для каждой вершины графа G получают в результате пересечения отображений этой вершины в исходных графах:

" х_i Î Х [ Г(х_i ) = Г₁ (х_i ) ? Г₂ (х_i )].

Для графов G₁ и G₂, изображающих на рис. 5.1 и 5.2 граф – пересечение G (его аналитическая, геометрическая и матричная формы), представлен на рис.5.5.