Определения, формы представления графов. Матричное представление графов. Матрица инциденций неориентированного графа, страница 2

Граф на рис. 2.1,б – подграф графа G, изображенного на рис. 2.1, а.

      Суграфом  G_р графа (Х, А) называется граф (Х, А_р), в котором А_р Ì А, т.е. суграф содержит то же самое множество вершин, что и исходный граф G, а множество дуг суграфа является подмножеством множества дуг исходного графа. Суграф G_р графа G приведен на рис. 2.1, в.

Для любой части G¹ графа G существует единственная дополнитель-ная часть – дополнение `G¹, состоящее из всех ребер графа  G, которые не принадлежат G¹.

          Дополнение `G<sub>s</sub> к подграфу G<sub>s</sub> приведено на рис. 2.1, г, дополнение `G_р к суграфу G_р – на рис. 2.1, д.

Упражнение

Для неориентированного графа с шестью вершинами привести примеры подгафов, суграфов и их дополнений.

3. ХАРАКТЕРИСТИКИ СВЯЗНОСТИ

В ориентированном графе к таким характеристикам относятся путь и контур.

Путем m  ориентированного графа называется последовательность дуг, в которой окончание каждой предыдущей дуги совпадает с началом следующей. Одна и та же дуга в пути может встречаться несколько раз. Если начальная вершина первой дуги в пути х_i, а конечная вершина  последней дуги х_j, то путь обозначают как m (x_i, x_j).

Путь называется простым, если в нем каждая дуга встречается только один раз, т.е. дуги не повторяются. Например, приведенные выше пути (а) и (б) являются простыми, так как дуга а₄ используется в нем дважды.

Примеры путей для графа на рис. 3.1:

m (х₂, х₆) = (а₄, а₁₀, а₈, а₇, а₉),             (а)

m (х₁, х₃) = (а₁, а₄, а₁₀, а₈,),                 (б)

m (х₁, х₆) = (а₁, а₄, а₁₀, а₈, а₅, а₄, а₉), (в)

Иногда путь удобно представить в виде последовательности вершин. Например, путь

(а): m (х₂, х₆) = (х₂, х₅, х₄, х₃, х₅, х₆).

Путь называется элементарным, если он не содержит повторяющихся вершин [путь (б) в графе на рис. 3.1]. Длиной пути  l(m) называется количество дуг, составляющих этот путь. Так, для графа рис. 3.1  l[m(х₂, х₆)] = 5, l[m(х₁, х₃)] = 4, l[m(х₁, х₆)] = 7.

Если каждой дуге орграфа (x_i, x_j) приписано какое-то число (вес) с_ij, означающее параметрическую характеристику (стоимость, надежность, время и т.д.), то граф называется графом со взвешенными дугами. Если число приписано вершинам графа, то граф называется графом со взвешенными вершинами. Если числа (веса) приписаны и дугам , и вершинам, то граф становится  взвешенным. Длина пути в графе со взвешенными дугами равна сумме длин (весов) всех дуг, входящих в путь, причем каждая дуга рассматривается столько раз, сколько она встречается в пути:

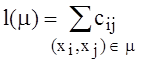
Контуром в орграфе называется замкнутый элементарный путь, т.е. путь, в котором начальная и конечная вершины совпадают. В графе на рис. 3.1 пути (а₄, а₁₀, а₈, а₅), (а₇, а₁₀, а₈) – контуры.

В неориентированном графе существуют понятия цепи и цикла, аналогичные понятиям, соответственно, пути и контура в орграфе.

Цепь – последовательность ребер, в которой ребра не повторяются, цикл – замкнутая цепь. Цикл называется простым, если в нем нет повторяющихся вершин. Цикл является элементарным, если он не содержит внутри себя других циклов. Цикл называется максимальным (минимальным), если содержит максимальное (минимальное) число ребер.

Примеры циклов для графа, приведенного на рис. 1.2:

(а_1, а₈, а_7, а₆₎, иначе (х₁, х₅, х_3, х_4,  х₁₎ – простой цикл, содержащийся в нем цикл (а₅, а₇, а₆), иначе (х₅, х₃, х_4, х₅), - элементарный; цикл (а₁, а_2, а₃, а₇, а₆) – максимальный, цикл (а₂, а₃, а₈) – минимальный.

Маршрут – понятие, справедливое для обоих типов графов. Это последовательность дуг (ребер) такая, что каждые две соседние дуги (два соседних ребра) имеют общую вершину, причем дуги (ребра)  и вершины могут повторяться. Пример маршрутов для графа рис. 1.,2: (а₂, а₄, а₇, а₃, а₄, а₆), (а₈, а₁, а₆, а₇, а₄), для графа рис. 3.1: (а₁, а₄, а₁₀, а₈, а₆), (а₄, а₁₀, а₈, а₇, а₉).

В практических задачах часто встречаются особые виды циклов: цикл Эйлера и цикл Гамильтона.

Цикл называется циклом Эйлера, если он содержит все ребра графа. Необходимым и достаточным условием существования цикла Эйлера является для неориентированного графа четность степеней всех его вершин, для ориентированного – равенство для каждой вершины полустепеней исхода и захода. Графы, изображенные на рис. 1.1, 1.2, 3.1, эйлерова цикла не содержат, т.к. не отвечают этим условиям.