Определения, формы представления графов. Матричное представление графов. Матрица инциденций неориентированного графа

1. ОПРЕДЕЛЕНИЯ, ФОРМЫ ПРЕДСТАВЛЕНИЯ ГРАФОВ

Граф G  задается множеством точек или вершин х₁, х₂,…х_n (которое обозначим через Х) и множеством отрезков а₁, а₂,…а_n (которое обозначим символом А) соединяющих между собой все или часть этих точек. Математически граф G полностью задается парой (Х, А): G = (Х, А).

Если отрезки из множества А ориентированы, что обычно показывается стрелками в геометрическом представлении графа, то они называются дугами, а граф называется ориентированным графом (орграфом) (рис.1.1). Если отрезки не имеют ориентации, то они называются ребрами, а граф –  неориентированным (рис. 1.2).

Часто употребляется другое, аналитическое описание орграфа [2]. Задается множество вершин Х и соответствие Г, которое показывает, как связаны между собой эти вершины. Соответствие Г называют отображением множества Х в Х, а граф тогда обозначается парой G = (Х, Г). Соответствие Г(х_i) – множество таких вершин х_j Î Х, для которых в графе G существует дуга (х_i, х_j). Дуга, отображающая вершину в саму себя, называется петлей (дуга а₄ на рис.1.1). Например, для вершин х₁, х₂, х₆ графа рис. 1.1  имеем :

Г(х₁) = {х₅, х₆},

Г(х₂) = {х₂, х₄},

Г(х₆) = Æ

Соответствие Г^-1(х_i) называют обратным (инверсным) соответствием, понимая под ним множество вершин х_к Î Х, для которых в G cуществует дуга (х_к, х_i). Для графа рис.1.1 Г^-1(х₁) = {х₅}, Г^-1(х₂) = {х₂,х₃},Г^-1(х₆)={х₁,х₅}.

В случае неориентированного графа или смешанного (содержащего и т.д. и дуги, и ребра) предполагается, что соответствие Г задает такой эквивалентный орграф, который получается из исходного заменой каждого ребра двумя противоположно направленными дугами, соединяющими те же самые вершины. Так, для вершин х₁ и х₂ графа на рис.1.2 имеем:

Г(х₁) = Г^-1 (х₁) = {х₂, х₄, х₅};  Г(х₂) = Г^-1 (х₂)  = {х₁, х₃, х₅}.

Отображение Г множества вершин Хк = {х₁, х₂,..., х_к} есть объединение отображений этих вершин:

Г(Х_к) = Г(х₁) U Г(х₂) U...U Г(х_к).

Например, для графа рис. 1.1 Г({х₁, х₂, х₆} ) = {х₂, х_4, х₅, х₆}; Г({х₃, х₄, х₅}) = {х₁, х_2, х_3,х₄, х₆ }.

Матричное представление графов осуществляется в виде матриц смежности и инциденций (инцидентности).

Две вершины х_i и x_j являются смежными, если есть дуга (ребро), соединяющая обе вершины. Дуга a называется инцидентной вершине х, если заходит в эту вершину или исходит из нее, и вершина х называется инцидентной такой дуге а.

          Матрица смежности А = [a_ij] орграфа G(Х, А) с n вершинами имеет размерность n ´ n и определяется следующим образом:

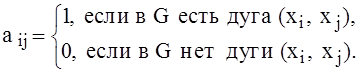
Матрица смежности для орграфа, изображенного на рис. 1.1, представлена на рис. 1.3.

   

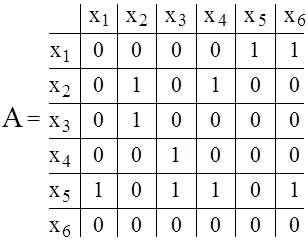
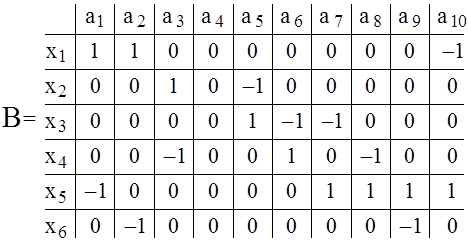
Рис. 1.3                                                            Рис. 1.4

Для неориентированного графа матрица смежности определяется так:

1, если вершины x_i  и x_j смежные,

0, в противном случае, т.е. матрица смежности неориентированного графа всегда симметрична. Матрица смежности графа рис. 1.2 представлена на рис. 1.5.

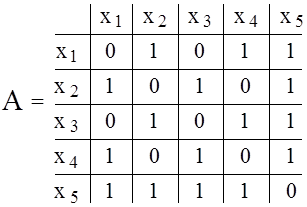
     Рис. 1.5

Матрица инциденций В = [b_ij]  орграфа G(Х, А) с n вершинами и m дугами имеет размерность n x m и определяется так:

1, если х_i является начальной вершиной дуги а_j,

-1, если х_i является конечной вершиной дуги а_j,

0, если а_j не инцидентнах х_i начальной вершиной дуги а_j.

Матрица инциденций для графа рис. 1.1 представлена на рис. 1.4. Для неориентированного графа матрица инциденций составляется так же, как и для орграфа, только все элементы, равные –1, заменяются на +1. Для графа рис.1.2 матрица инциденций приведена на рис. 1.6.

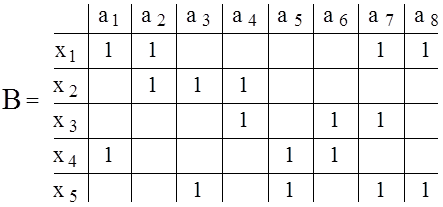
Рис. 1.6

Степень d вершины x_i  неориентированного графа есть число ребер, инцидентных этой вершине. Для графа рис. 1.2

d(x₁) = d(x₂) = d(x₃) = d(x₄) = 3;  d(x₅) = 4.

В ориентированном графе степень вершины х_i характеризуется двумя числами: полустепенью исхода, равной числу дуг, исходящих из х_i, и полустепенью захода, равной числу дуг, входящих в х_i.

Упражнения

1. Чему равна сумма элементов i-й строки в матрице смежности орграфа , i – го столбца?

2.  Изменится ли матрица смежности орграфа, если пренебречь ориентацией дуг?

3.Что представляет собой  матрица инциденций неориентированного графа:  сумма элементов i-й  строки, i-го столбца?

4. Неориентированный  граф  G(X, A) задан матрицей смежности А.

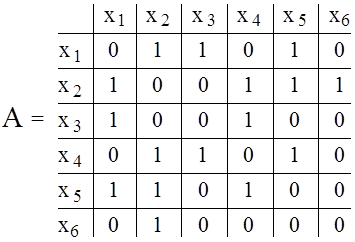
Привести геометрическое и аналитическое представление графа, построить матрицу инциденций.

5. Чему равна сумма степеней всех вершин неориентированного графа?

6. Что определяет сумма полустепеней исхода всех вершин орграфа, сумма полустепеней захода?

7. Доказать, что в неориентированном графе число вершин с нечетной степенью четно (нуль – четное число).

8. Можно ли из полного графа с 17 вершинами удалить некоторые ребра так, чтобы степень каждой вершины равнялась пяти?

2.ЧАСТИ ГРАФОВ

Граф G¢(X,¢ A¢) называется частью графа G(X, A), если Х¢ Í Х, А.

Рассмотрим два вида частей: подграф (порожденный подграф) и суграф (остовный подграф).

Подграфом G графа  G(Х, Г) называется граф (Х_s, Г_s), в который входит лишь часть вершин графа G, образующих множество Х_s, вместе с дугами, соединяющими эти вершины, т.е. Х_s Ì Х и для каждой вершины х_i Î Х_s Г_s(х_i) = Г(х_i) Õ Х_s