Оптимальная фильтрация сигналов. Спектральная функция детерминированного аналогового сигнала

МОПО                                                                                                                                                       РФ

РГРТА

КАФЕДРА ТОР

КУРСОВАЯ  РАБОТА

“Оптимальная фильтрация сигналов”

Выполнил:       

Проверил:                    

Рязань 2000г.

Цель курсовой работы: Определение и расчет по заданному сигналу характеристик согласованого фильтра, построение структурных схем и вычисление отношения исгнал/шум на входе и выходе оптимального фильтра. 

Задание:Вариант 9;

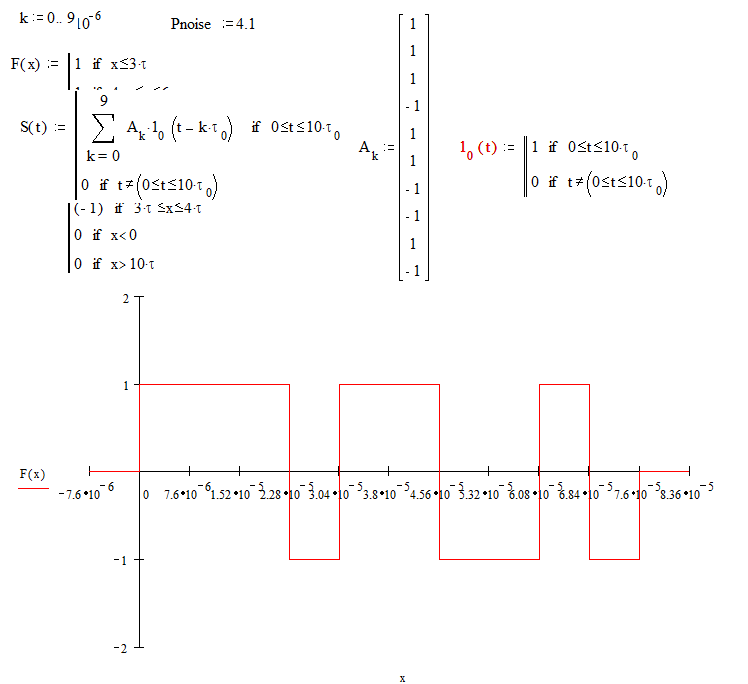
1₀(t)-Единичный импульс.  A_k-Амплитуда k-го импульса

I. Задание на курсовую работу.

При выполнении курсовой работы должны быть определены, вычислены и графически построены следующие параметры и характеристики сигнала и согласованного фильтра.

1.  Аналитические выражения спектральной функции S(w), амплитудного ½ S(w)½ и фазового ½Y(w)½ спектров заданного сигнала.

2.  Численное значение величины шага частоты Df при вычислениях на ЭВМ спектров сигнала.

3.  Численные значения ½ S(w)½ и ½Y(w)½, при 2..3 значениях частоты f для контроля дальнейших вычислений с помощью ЭВМ.

4.  Рассчитанные на ЭВМ амплитудный ½ S(w)½ и фазовый ½Y(w)½ спектры и их графические диаграммы.

5.  Значение верхней граничной частоты f_в спектра сигнала, определенное из условия                    ½ S(2pf)½£0.1·½ S(2pf)½_max при f ³f_в

6.  Дискретный аналог (в узловых точках) АКФ Ks(n) заданного сигнала S(t) и его график.

7.  Дискретный аналог ВКФ Ksu(n) заданного сигнала S(t) и сигнала U(t), у которого два любых единичных импульса изменили полярность на противоположную, его график.

8.  Аналитические выражения комплексного коэффициента передачи согласованного фильтра Нопт(w), его АЧХ и ФЧХ, импульсной характеристики согласованного фильтра g(t).

9.  Графики АЧХ и импульсной характеристики согласованного фильтра.

10.  Варианты структурных схем согласованного фильтра [С1] .

11.  Эпюры колебаний на выходе каждого элементарного блока структурной схемы согласованного фильтра при воздействии на его вход дельта функции.

12.  Аналитическое выражение энергетического спектра случайного процесса Fвых(f) на выходе согласованного фильтра при воздействии на его вход квазибелого шума с заданной мощностью, результаты расчетов значений Fвых(f) в зависимости от значений частоты f при заданном шаге Df : график Fвых(f).

13.  Эффективная (энергетическая) ширина спектра сигнала Dfэф и его база m.

14.  Значения отношения сигнал/шум на входе и выходе согласованного фильтра.

15.  Дискретное представление входного сигнала и импульсной характеристики в соответствии с теоремой Котельникова (временные диаграммы).

16.  Спектральная диаграмма дискретного сигнала с ограниченным спектром.

17.  Численные и графические результаты расчета на ЭВМ сигналов на выходе дискретного согласованного фильтра при воздействии на его вход:

1) дискретного сигнала в соответствии с п.15;

2) дискретного сигнала, у которого два любых единичных импульса изменили полярность на противоположную.

II. Краткие теоретические сведения.

Спектральной функцией детерминированного аналогового сигнала S(t) называется функция S(w), вычисляемая с помощью прямого преобразования Фурье:

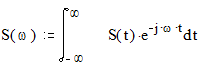Задание спектральной функции S(w) однозначно определяет сигнал как функцию времени через обратное преобразование Фурье:

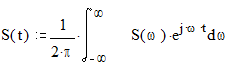Т.о. имеет место пара преобразований Фурье S(t)«S(w).

Спектральная функция S(w) в общем, является комплексной функцией и может быть представлена в виде

где

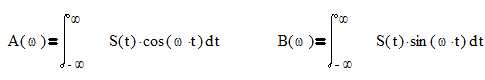Модуль и аргумент спектральной функции определяются выражениями

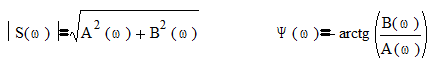Выражение (3.5) определяет амплитудный и фазовый спектры сигнала S(t). Выражения (3.2) можно преобразовать к виду

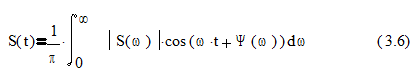откуда следует, что импульсный сигнал S(t) допустимо рассматривать в виде суммы бесконечно большого числа гармонических составляющих с непрерывно изменяющейся частотой и бесконечно малыми амплитудами. При этом ½ S(w)½ является спектральной плотностью распределения амплитуд гармонических составляющих по частоте, а Y(w) показывает распределение начальных фаз гармонических составляющих по частоте. Из (3.5) следует, что при w=0 S(0)=A(0) и B(0)=0 т.е А(0) равен площади под кривой S(t). Энергия сигнала S(t) определяется равенством Парсеваля.