 |
Где ½ S(w)½2 есть энергетический спектр сигнала S(t), показывающий распределение сигнала по частоте.
Важную роль в описании детерминированных сигналов S(t) играет её автокорреляционная функция (АКФ) определяемая в виде:
 |
Здесь Еs энергия сигнала S(t) . АКФ связана с энергетическим спектром ½ S(w)½2 преобразованием Фурье:
 |
Отклик S2(t) линейной стационарной системы (фильтра) на воздействие S1(t) может быть найден следующим образом:
 |
S1(t)«S1(w) ; g(t) «H(w)
H(w) и g(t) есть комплексный коэффициент передачи и импульсная характеристика линейной системы.
При воздействии на линейный фильтр аддитивной смеси известного сигнала и белого шума S(t)+X(t) можно получить на выходе наибольшее возможное отношение пикового значения сигнала к среднеквадратическому значению шума, если комплексный коэффициент передачи такого фильтра определяется выражением:
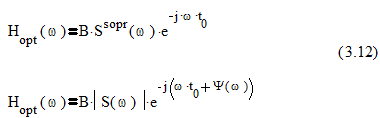 |
Здесь S*(w)=Ssopr(w) – комплексно-сопряженный спектр входного сигнала,
B- постоянный коэффициент, учитывающий размерность,
t0- время при котором отношение с/ш становится максимально возможным.t0³tи.
где tи-длительность входного сигнала.
Фильтр, коэффициент передачи которого определяется выражением (3.12), называется оптимальным или согласованым.Импульсная характеристика ОФ определяется как функция gopt(t)=B*S(t0-t); (3.13)
т.е. импульсная характеристика ОФ по своей форме должна совпадать с зеркальным отображением сигнала.
Форма сигнала на выходе ОФ может быть найдена в соответствии с выражениями (3.10) и (3.11), что в результате даёт:
Итак, сигнал на выходе ОФ с точностью до постоянного коэффициента B совпадает с АКФ входного сигнала S(t). В момент времени t=t0 ,т.е при t=0 выходной сигнал имеет пиковое значение Sвых(t0)=B*Ks(0)=B*Es
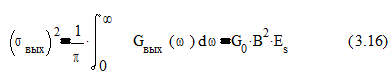 |
 |
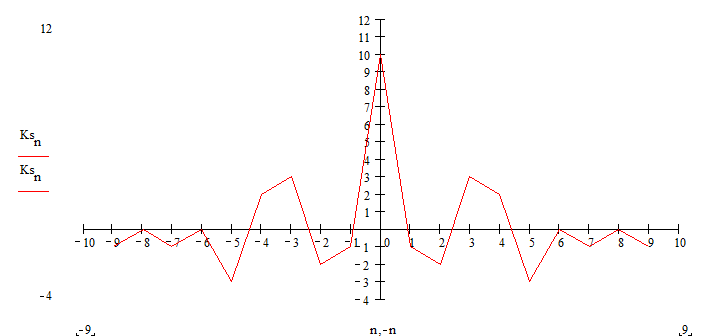
При использовании сложных сигналов, в частности бинарных кодовых последовательностей (рис 1), их АКФ имеет один узкий центральный пик и боковые лепестки более низкого уровня (рис 2).
Под базой сигнала m понимают произведение эффективной ширины спектра сигнала на его длительность:
Под эффективной (энергетической) шириной спектра
сигнала обычно подразумевают диапазон частот, в котором сосредоточена основная
доля энергии сигнала. Для рассматриваемых ФКМ сигналов можно считать, что:
Если на входе ОФ действует квазибелый шум ограниченной мощности Pш=4.1 В2
со спектром, распределенным равномерно в полосе Dfэф , то спектральная плотность мощности шума определяется в виде:
 |
Тогда, используя формулу (3.17), получаем
Энергию сигнала можно выразить в виде Es=Ps*tи , где Ps-средняя мощность входного сигнала.
Окончательно отношение с/ш на выходе ОФ будет равно:
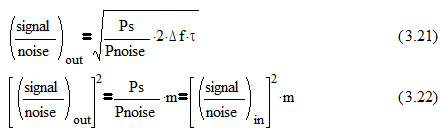 |
III. Выполнение расчета.
1. Аналитические выражения спектральной функции ![]() , амплитудного спектра
, амплитудного спектра ![]() , и фазового
, и фазового ![]() спектров
заданного сигнала.
спектров
заданного сигнала.
Путем дифференцирования сводим исходный ФКМ (рис. а) сигнал к линейной комбинации дельта-функций (рис. б):
S’(t) 2d(t-4t0) 2d(t-8t0)
d(t) d(t-10t0)
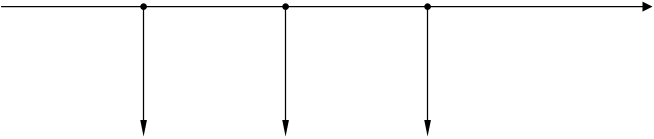 |
0 t0 2t0 3t0 4t0 5t0 6t0 7t0 8t0 9t0 10t0 t,мкс
-2d(t-3t0) -2d(t-6t0) -2d(t-9t0)

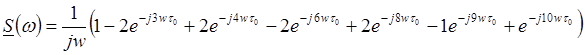
Так как ![]() , имеем:
, имеем:
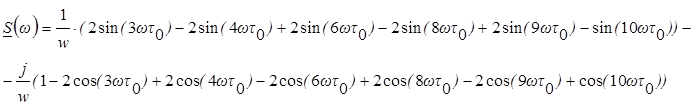
Определим A(w) и B(w):
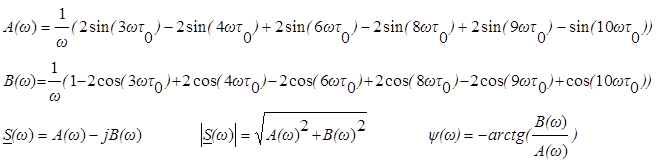
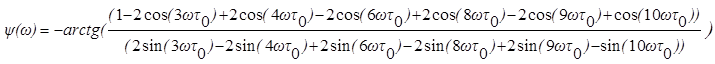
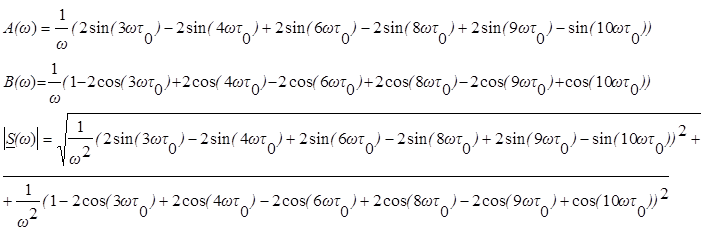
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.