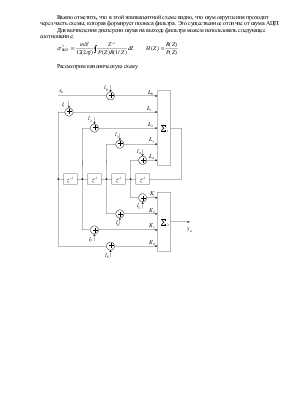





Важно отметить, что в этой эквивалентной схеме видно, что шум округления проходит через часть схемы, которая формирует полюса фильтра. Это существенное отличие от шума АЦП.
Для вычисления дисперсии шума на выходе фильтра можем использовать следующее соотношение:
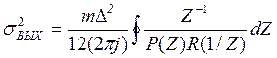
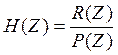
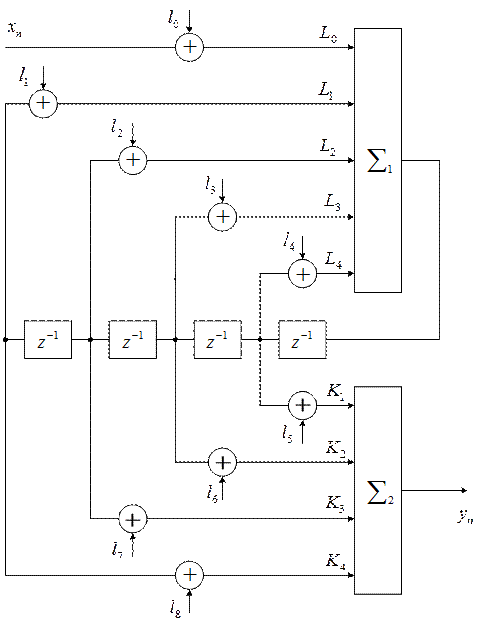
Рассмотрим каноническую схему
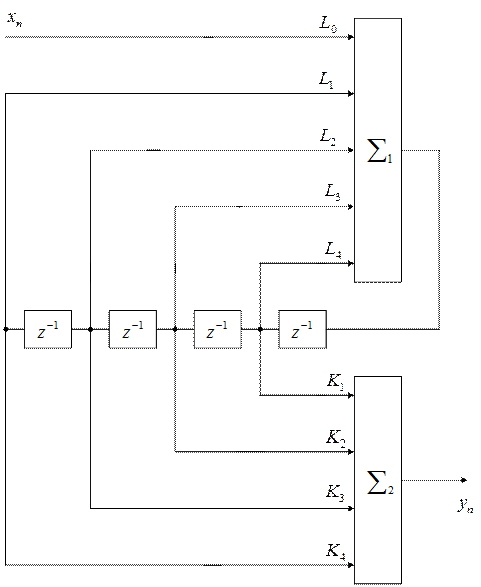
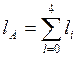
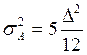 и
и 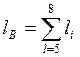
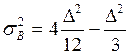
![]() , где
, где 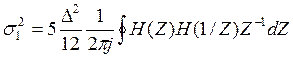
В 1-ой и во 2-ой схеме коэффициент усиления для сигнала и для шума различны, т.к. сигнал проходит обе части схемы, а шум имеет свой путь.
В ФНЧ и ПФ эффект, вызванный нулями передаточной функции в полосе заграждения, уменьшает шум, а полюсы в полосе пропускания увеличивают шум. Поэтому может показаться, что прямая форма вводит больше шума, чем каноническая, т.к. в прямой форме шум проходит через часть схемы, формирующей полюсы. А в канонической как через полюса, так и через нули. Но все не так просто, наличие нулей с малым коэффициентом усиления в прямой форме реализации означает, что и уровень сигнала тоже уменьшится. А т.к. при проектировании фильтров основной задачей является уменьшение разрядности регистров, то необходимо сопоставлять не только величину шума, но и уровень сигнала.
Эффект мертвой зоны.
До сих пор мы полагали, что ошибки, вызываемые каждым округлением, некоррелированные случайные величины, но это бывает не всегда. Факт коррелированности ошибок округления может приводить в различным неприятным эффектам.
Рассмотрим фильтр 1-го порядка.
![]()
![]()
Будем считать, что на входе
фильтра ![]() , шаг округления до ближайшего целого
, шаг округления до ближайшего целого ![]() , начальные условия
, начальные условия ![]() .
Если для этих величин посчитать без округления, то
.
Если для этих величин посчитать без округления, то ![]() .
.
|
N |
0 |
1 |
2 |
|
|
|
До |
264,4 |
263,44 |
263,48 |
261,52 |
|
|
После |
264 |
263 |
262 |
262 |
Теперь будем считать ![]()
|
N |
0 |
1 |
|
|
|
До |
245,2 |
245,5 |
245,2 |
|
|
После |
245 |
245 |
245 |
![]() то
такое значение и будет установившееся независимо то входного сигнала. Это и
называется мертвая зона.
то
такое значение и будет установившееся независимо то входного сигнала. Это и
называется мертвая зона.
Если сигнал станет равен нулю, сигнал на выходе не упадет, а останется в этой мертвой зоне. У фильтров более высокого порядка возможны более сложные эффекты. Например, будут возникать стационарные колебания. Рассмотрим фильтр 2-го порядка:
![]()
![]()
|
N |
0 |
1 |
2 |
|
|
|
До |
-1,6 |
1,6 |
-1,6 |
1,6 |
|
|
После |
-2 |
2 |
-2 |
2 |
Возникают колебания с частотой ![]() . Их смысл в том, что каждый раз после
итерации появляется шумовой отсчет и фильтр усиливает этот шум отсчет на частоте
. Их смысл в том, что каждый раз после
итерации появляется шумовой отсчет и фильтр усиливает этот шум отсчет на частоте
![]() до тех пор пока не будет достигнут уровень
квантования
до тех пор пока не будет достигнут уровень
квантования ![]() .
.
Цифровая обработка случайных сигналов
С обработкой случайных сигналов приходится иметь дело в любой РЭС. Обработка таких сигналов производится с самыми различными целями. Наиболее типичной задачей обработки является оценка различных характеристик случайного сигнала (мат ожидание, дисперсия, корреляционная функция, законы распределения, спектральная плотность мощности и т.д.).
Оценка моментов.
Здесь ограничимся рассмотрением стационарного эргодического процесса.
Оценка мат ожидания
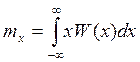 , где
, где ![]() - функция плотности распределения
вероятности.
- функция плотности распределения
вероятности.
Для стационарного эргодического процесса может быть записано:
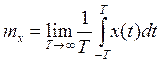 , для
дискретного сигнала:
, для
дискретного сигнала: 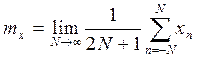
В качестве оценки мат ожидания ![]() обычно используют
обычно используют
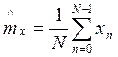 -
выборочное среднее. N - должно быть достаточно велико
-
выборочное среднее. N - должно быть достаточно велико ![]() является случайной величиной, которая
имеет свой закон распределения и свои моменты.
является случайной величиной, которая
имеет свой закон распределения и свои моменты.
Если ![]() - это
мат ожидание оценки, то оценка несмещенная. Мат ожидание, дисперсия и скорость
сходимости оценки являются ее главными характеристиками.
- это
мат ожидание оценки, то оценка несмещенная. Мат ожидание, дисперсия и скорость
сходимости оценки являются ее главными характеристиками.
Качество оценки определяется степенью ее разброса от истинного значения.
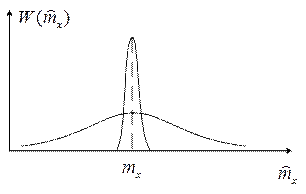
Оценка в зависимости от того как ведет себя ее дисперсия при увеличении объема выборки бывает состоятельной и несостоятельной. Если при росте объема выборки дисперсия оценки стремится к нулю, то она является состоятельной, если же этого не наблюдается, то это несостоятельная оценка
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.