.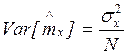
На практике часто используют оценки максимального отношения правдоподобия. Эта оценка основана на анализе совместно закона распределения, рассмотрим этот закон:
![]() .
.
Оценка максимума правдоподобия
–это такое значение ![]() , при котором
, при котором ![]() становиться максимальным.
становиться максимальным.
Уравнение максимума правдоподобия имеет вид:
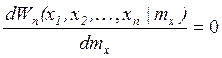 , где
, где
![]() - оценка max правдоподобия.
- оценка max правдоподобия.
При вычислении этой оценки
предположим, что ![]() - независимые случайные величины,
тогда
- независимые случайные величины,
тогда
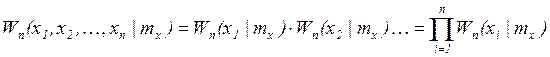
Отношение правдоподобия равно ![]() .
.
Если этот метод применить к нормальному закону распределения, то
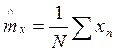
Оценка дисперсии
Для оценки дисперсии нормального стационарного случайного процесса:
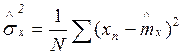 Мат
ожидание для этой оценки имеет вид
Мат
ожидание для этой оценки имеет вид 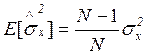 , т.е. оценка дисперсии
является смещенной, но при росте N это смещение
стремиться к нулю, поэтому эту оценку называют асимптотически не смещенной.
Т.к. нам известен коэффициент искажений, то оценку можно скорректировать:
, т.е. оценка дисперсии
является смещенной, но при росте N это смещение
стремиться к нулю, поэтому эту оценку называют асимптотически не смещенной.
Т.к. нам известен коэффициент искажений, то оценку можно скорректировать:
 - это
уже несмещенная оценка.
- это
уже несмещенная оценка.
Дисперсия оценки дисперсии имеет вид:
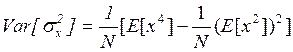 она
состоятельная.
она
состоятельная.
При численной оценке мат
ожидания и дисперсии могут возникнуть дополнительные погрешности в том случае,
если вычислительное устройство работает с небольшим числом разрядов. При
большом объеме выборок N начиная
с некоторого номера отсчета порядок, т.е. число разрядов суммы будет
существенно больше числа разрядов слагаемых. В результате произойдет потеря
точности. Это происходит из-за того, что при суммировании чисел происходит
выравнивание порядков. Т.е мантисса числа с меньшим порядком сдвигается вправо
на количество разрядов равное разности порядков суммируемых чисел. Если эта
разность велика, то часть или все разряды слагаемого могут выйти за разрядную
сетку вычислителя. Поэтому при цифровой обработке, чтобы избежать этого
эффекта, можно использовать более сложные алгоритмы вычисления. Этот алгоритм
используется если ![]() . Введем новую функцию
. Введем новую функцию 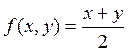 .
.
Есть массив чисел ![]()
Алгоритм имеет вид:
1. ![]()
2. ![]()
3. если ![]() идти на (2)
идти на (2)
4. ![]()
5. ![]() ,
,![]()
6. ![]()
7. если ![]() идти на (6)
идти на (6)
8. если ![]() идти на (5)
идти на (5)
9. ![]()
В этом алгоритме мы все время складываем два числа, порядки которых близки, поэтому потери точности не происходит. Кроме того есть особенности при вычислении дисперсии:
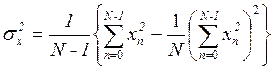
Однако слагаемые в скобках при
вычислении могут оказаться близкими по порядку. При небольшом числе значащих
цифр и при N ![]() оба числа
будут одного порядка и при вычислении число которое представляет дисперсию
будет содержать мало значащих цифр т.о. происходит потеря точности.
оба числа
будут одного порядка и при вычислении число которое представляет дисперсию
будет содержать мало значащих цифр т.о. происходит потеря точности.
Исходная формула менее чувствительна к этому эффекту, но вычисления по ней требуют большего объема памяти и времени.
Оценка законов распределения.
Рассмотрим оценки дифференциальных законов распределения (ФПВ). Для их оценки используется параметрические и непараметрические оценки. Не параметрический подход используется когда нет никакой априорной информации о типе закона распределения. Но некоторые предположения должны быть, например, что он непрерывный. Методы:
1. Гистограммный
2. Метод Парзена
3. Метод разложения по базисным функциям
4. Метод полиномов Смирнова
5. Метод К-ближайших соседей
Гистограммный метод получил самое большое распространение. Применяется для априорно непрерывных законов распределения плотности вероятности и отличных от нуля на всем рассматриваемом множестве значений аргумента x.
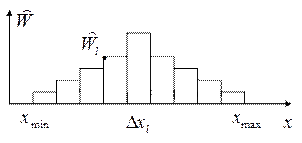
![]() -
площадь под гистограммой.
-
площадь под гистограммой.
Этот признак используется для
проверки правильности. На выбор величины интервалов есть практические
рекомендации. Обычно их число 10, 12, 15 при ![]()
Достоинством гистограммного метода является простота оценивания и ясный физический смысл оценки. Здесь не нужно никакой априорной информации о ФПВ. Используется два допущения: отсутствие скачков и положительная определенность ФПВ.
Недостатки: если N велико, а количество интервалов неизменно, то оценка
сходится не самой ФПВ, а интегралу от нее 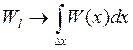 .
.
Т.е. эта оценка не состоятельная, однако есть методы позволяющие обойти эту неприятность. Для того, чтобы оценка сошлась к точному значению ФПВ, должны выполниться три условия:
1. ![]()
2. ![]()
3. 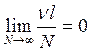
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.