Спектральный анализ непериодических сигналов. Непериодические управляющие сигналы. Сигнал – треугольный видеоимпульс

1. Введение.

Среди разнообразных систем ортогональных функций, которые могут использоваться в качестве базисных для представления радиотехнических сигналов, особое место занимают гармонические функции. Важность гармонических сигналов для радиотехники обусловлена рядом причин. В частности, гармонические сигналы инвариантны относительно преобразований, осуществляемых линейными электрическими цепями. Если на входе такой электрической цепи действуют гармонические колебания, то сигнал на ее выходе также остается гармоническим, отличаясь от входного лишь амплитудой и начальной фазой. Кроме того, техника генерирования гармонических сигналов относительно проста.

Если какой-либо сигнал представлен в виде суммы гармонических колебаний с различными частотами, то говорят, что осуществлено спектральное разложение этого сигнала в базисе гармонических функций. Сумма отдельных гармонических компонент сигнала образует его спектр.

Спектральное представление сигнала можно получить, используя разложение в ряд Фурье:

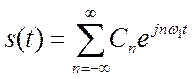       (1)

с коэффициентами

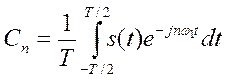  (2)

2. Спектральный анализ непериодических сигналов.

Использование разложение в ряд Фурье, легко перейти от периодического сигнала к одиночным импульсам. Для этого следует устремить к бесконечности период повторения T. При этом частоты соседних гармоник nw₁ и (n+1)w₁ окажутся сколь угодно близкими, так что в формулах (1) и (2) дискретную переменную nw₁ можно заменить на непрерывную переменную w – текущую частоту. Амплитудные коэффициенты С_n становятся неограниченно малыми    из-за наличия величины T в знаменателе формулы (2).

В результате получим величину

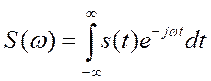     (3), которая носит название спектральной плотности сигнала s(t). Формула (3) называется преобразованием Фурье данного сигнала.

2.1. Непериодические управляющие сигналы.

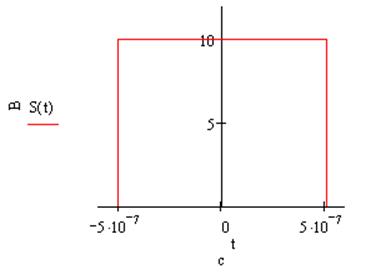
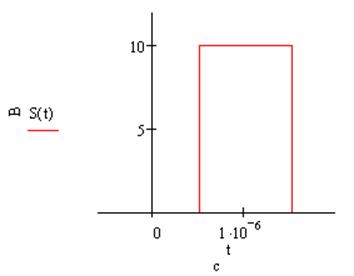
2.1.1. Сигнал – прямоугольный видеоимпульс (рис. 1).

Используя формулу (3), можно получить спектральную плотность прямоугольного видеоимпульса:

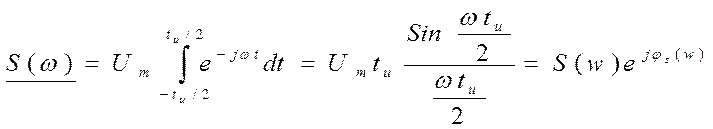, где

Фазовый спектр

Амплитудный спектр

 

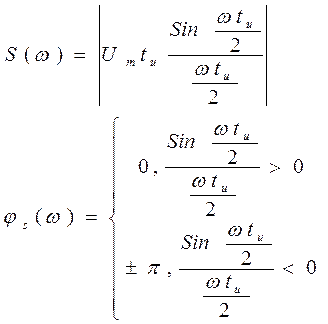
Для записи аналитического выражения такого сигнала необходимо использовать функцию включения:

u(t) = U_m 1(t + t_u/2) - U_m 1(t - t_u/2)

Параметры:

U_m=10В, t_u=1,01 мкс

1)Записать аналитическое выражение для сигнала s(t). Рассчитать и построить сигналы s(t), - s(t), s(0.5t), s(2t), s(t-t_u) и их амплитудные и фазовые спектры.

s(t) = 10[ 1(t + 0.505×10^-6) - 1(t - 0.505×10^-6)]

-s(t) = -10[ 1(t + 0.505×10^-6) - 1(t - 0.505×10^-6)]

s(0.5t) = 10[ 1(0.5t + 0.505×10^-6) - 1(0.5t - 0.505×10^-6)]

s(2t) = 10[ 1(2t + 0.505×10^-6) - 1(2t - 0.505×10^-6)]

s(t-t_u) = 10[ 1(t – 0.505×10^-6) - 1(t - 1.515×10^-6)]

Амплитудные и фазовые спектры данных сигналов:

s(t):

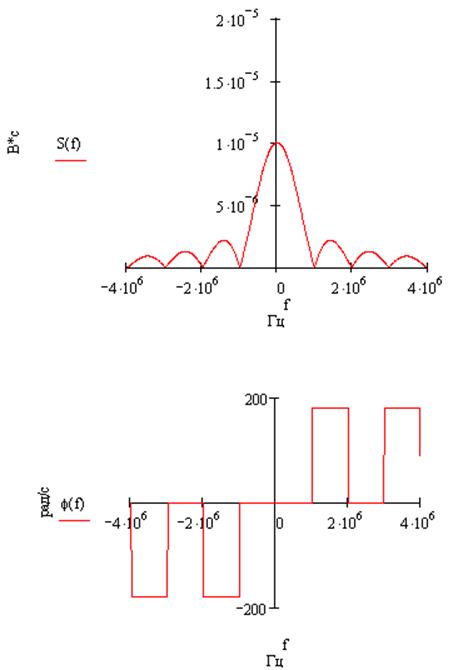
-s(t):

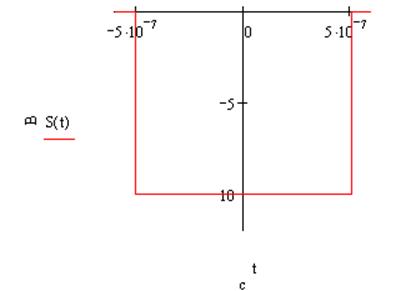
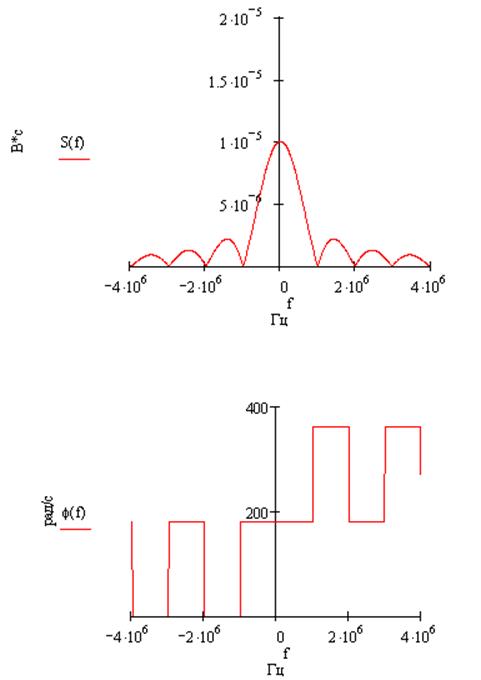
s(0.5t):

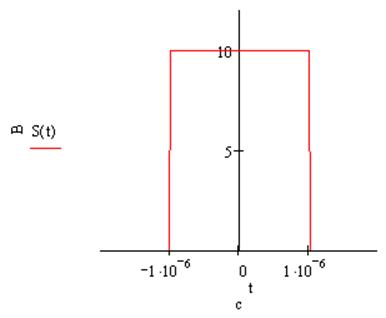
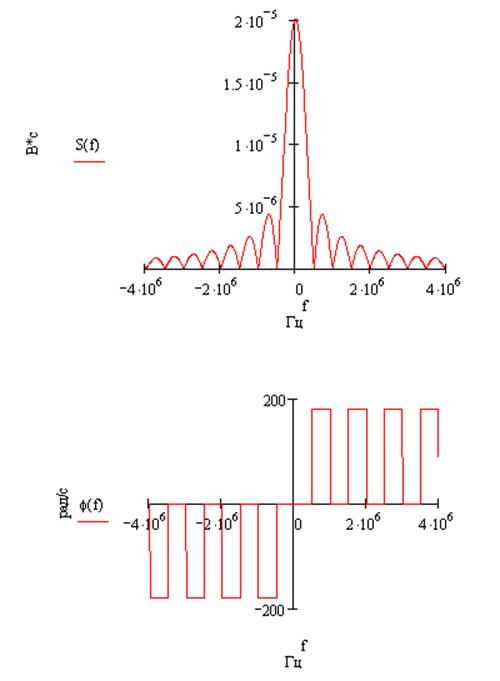
s(2t):

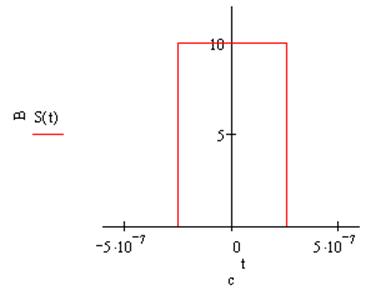
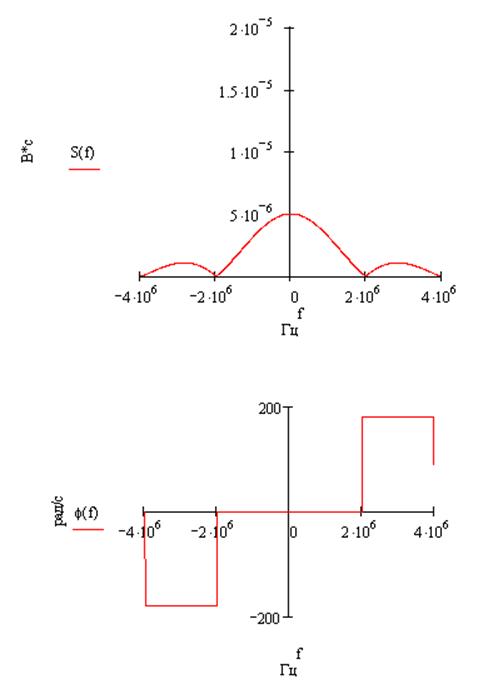
s(t-tи):

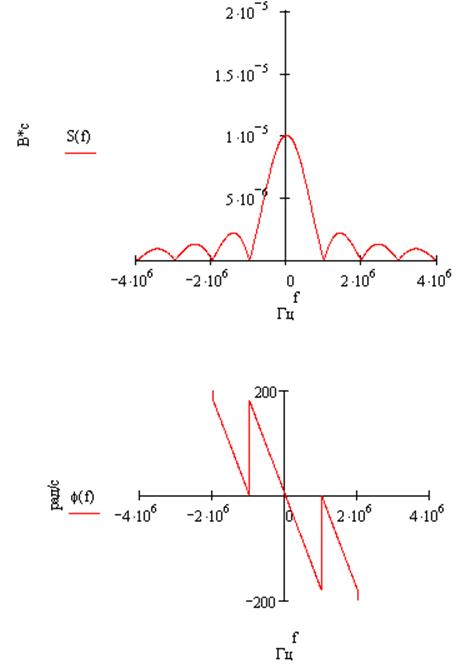
Рассчитаем энергию и максимальную мгновенную мощность колебания s(t) в сопротивлении 1 Ом.

p(t)_max=s²(t)_max

p(t)= 10²=100 Вт

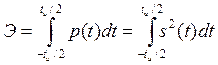
Э=100× t_u=101×10^-6 Дж

Выводы: на основе графиков сигналов, амплитудных и фазовых спектров можно сделать выводы, что при s(t)=-s(t) изменение амплитудного спектра не происходит, зато фазовый спектр смещается на  вверх относительно оси абсцисс. При уменьшении сигнала во временной области в 2 раза амплитудный спектр становиться уже в 2 раза и его максимум возрастает в 2 раза, фазовый спектр становиться уже в 2 раза. При увеличении сигнала во временной области в 2 раза амплитудный спектр становиться шире в 2 раза и его максимум уменьшаеться в 2 раза, фазовый спектр становиться шире в 2 раза. При смещении сигнала на величину -tи изменение амплитудного спектра не происходит, зато происходит смещение фазового спектра на величину -.

2.1.2.Сигнал – треугольный видеоимпульс (рис. 8).

 

Продифференцируем данный сигнал:

 

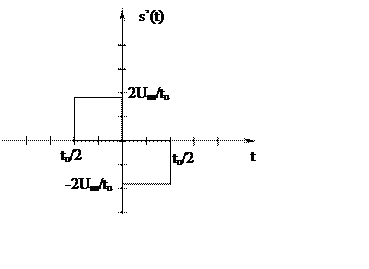Тогда на основе формулы (3) и свойств преобразований Фурье получим:

S_пр(w)=S₁(w)+S₂(w)

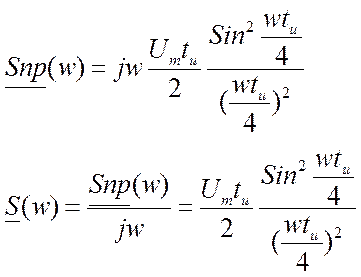
Аналитическое выражение для треугольного видеоимпульса выглядит следующим образом:

u(t)=(2U_m/t_u ) × (t+t_u/2) ×1(t+t_u/2)- (2U_m/t_u ) ×(t+t_u/2) ×1(t) - (2U_m/t_u ) × (t-t_u/2) ×1(t)+

+(2U_m/t_u ) ×(t-t_u/2) ×1(t-t_u/2)

u(t)= (2U_m/t_u ) ×{(t+t_u/2) × [1(t+t_u/2)- 1(t)]+ (t-t_u/2) × [ 1(t-t_u/2)-1(t)]}

Параметры:

U_m=10В, t_u=1,01 мкс

1) Записать аналитическое выражение для сигнала s(t). Рассчитать и построить сигналы s(t), -s(t), s(0.5t), s(2t), s(t-t_u) и их амплитудные и фазовые спектры.

s(t)= 19.8×10⁶ ×{(t+0.505×10^-6) × [1(t+0.505×10^-6)- 1(t)]+ (t-0.505×10^-6) ×                                  × [ 1(t-0.505×10^-6)-1(t)]}

-s(t)= -19.8×10⁶ ×{(t+0.505×10^-6) × [1(t+0.505×10^-6)- 1(t)]+ (t-0.505×10^-6) ×                      × [ 1(t-0.505×10^-6)-1(t)]}

s(2t)= 19.8×10⁶ × {(2t+0.505×10^-6) × [1(2t+0.505×10^-6) - 1(2t)] + (2t-0.505×10^-6) ×                    × [ 1(2t-0.505×10^-6) - 1(2t)]}

s(0.5t)= 19.8×10⁶ × {(0.5t+0.505×10^-6) × [1(0.5t+0.505×10^-6) - 1(0.5t)] + (0.5t-0.505×10^-6) ×     × [ 1(0.5t-0.505×10^-6) - 1(0.5t)]}

s(t-t_u)= 19.8×10⁶ × {(t-0.505×10^-6) × [1(t-0.505×10^-6) - 1(t-1.01×10^-6)] + (t-1.515×10^-6) ×                × [ 1(t-1.515×10^-6) - 1(t-1.01×10^-6)]}

Амплитудные и фазовые спектры данных сигналов:

s(t):

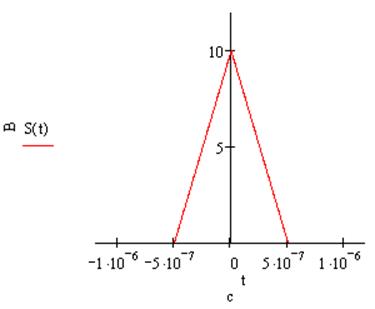
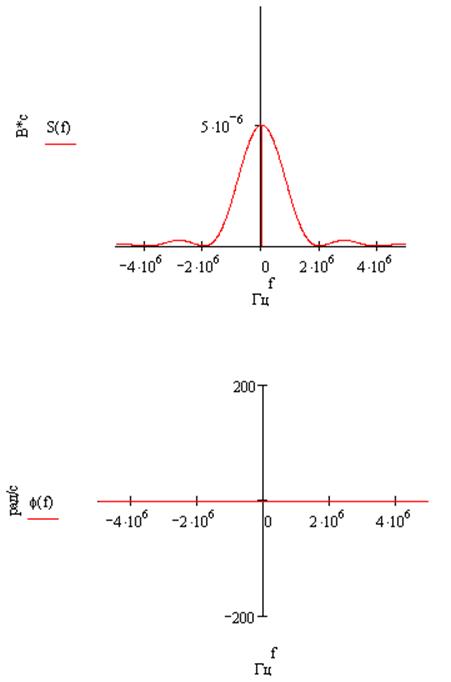
-s(t):

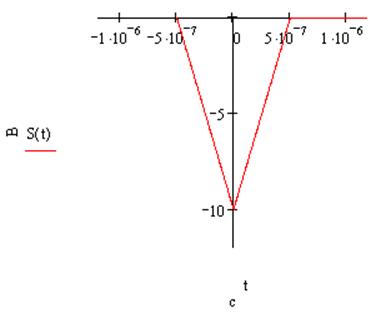
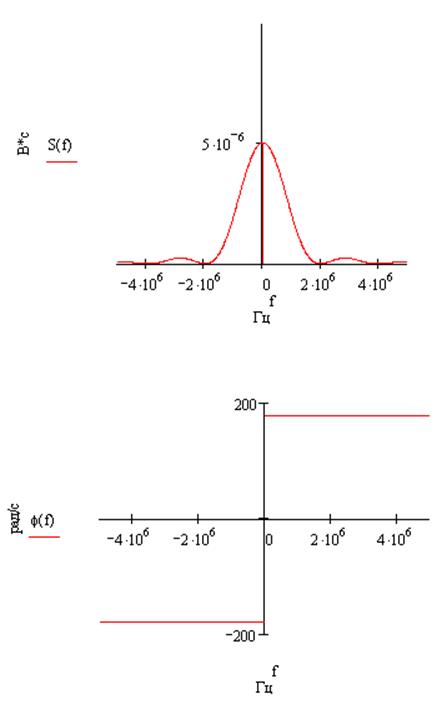
s(0.5t):

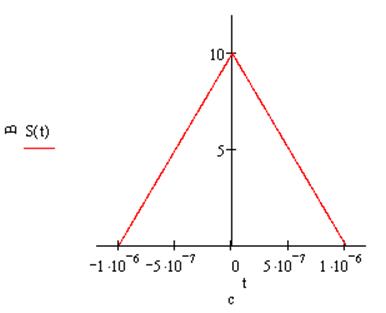
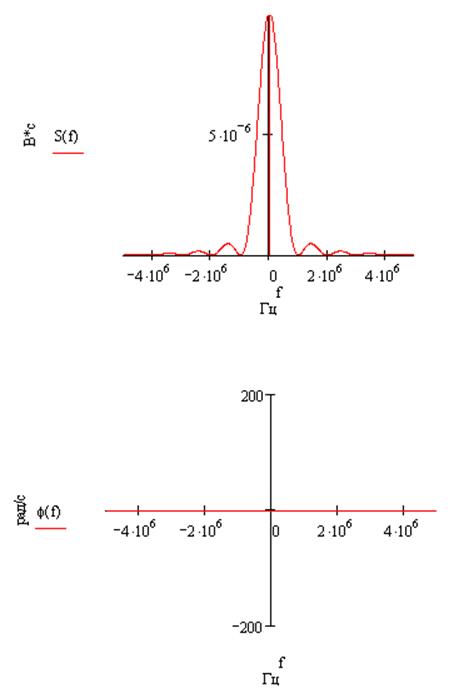
s(2t):

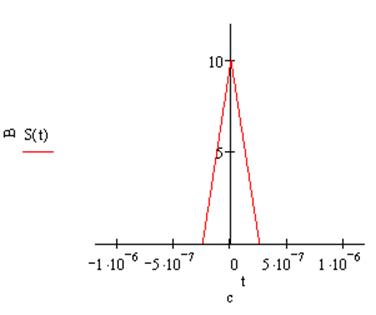
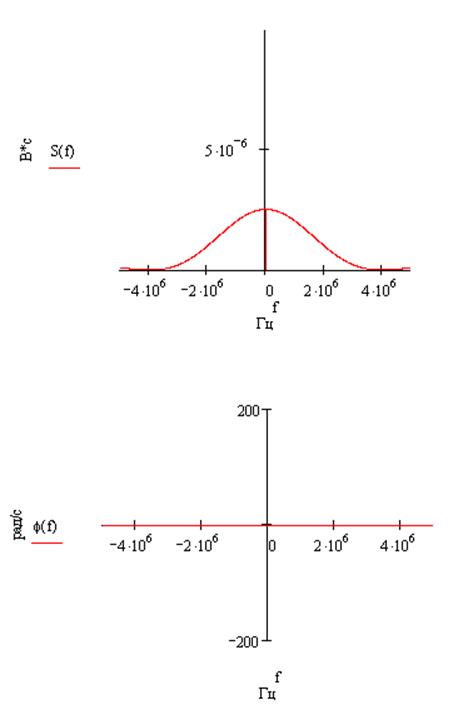
s(t-tи):

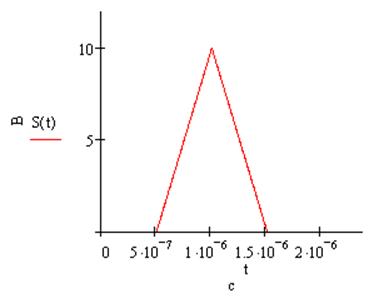
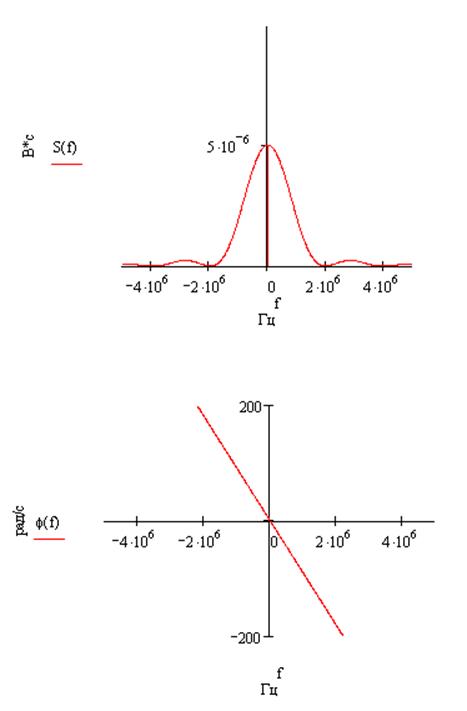
Рассчитаем энергию и максимальную мгновенную мощность колебания