Главные и побочные определители. Алгебраические дополнения элементов транспонированной матрицы

КОНТРОЛЬНАЯ РАБОТА 1

1.       Вычислить определитель а)  разложив по 1 строке

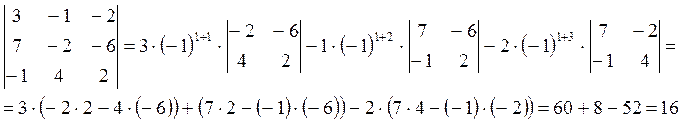
б)  используя основные свойства

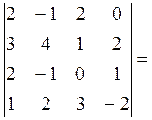
Поменяем местами первую и четвертую строки (при этом знак определителя сменим на противоположный):

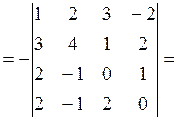
Элементы первой строки умножим на (-3) и прибавим их к соответствующим элементам второй строки. Элементы первой строки умножим на (-2) и прибавим их к соответствующим элементам третьей и четвертой строк:

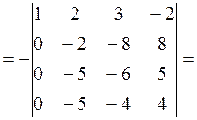
Из второй строки вынесем множитель (-2), при этом каждый элемент данной строки делим на (-2):

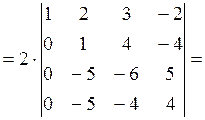
Элементы второй строки умножим на 5 и прибавим их к соответствующим элементам третьей и четвертой строк:

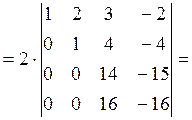
Поменяем местами третью и четвертую строки (при этом знак определителя сменится на противоположный):

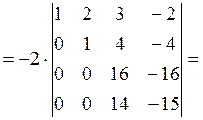
Из третьей строки вынесем множитель 16, при этом каждый элемент данной строки делим на 16:

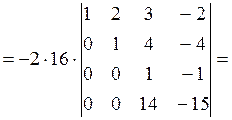
Элементы третьей строки умножим на (-14) и прибавим их к соответствующим элементам четвертой строки:

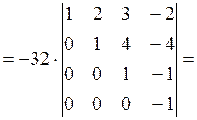
Определитель матрицы треугольного вида (под главной диагональю стоят только нули) равен произведению элементов главной диагонали. Окончательно получим:

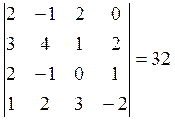
12.     Выполнить действия над матрицами:

, , ,

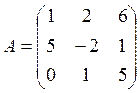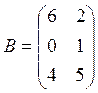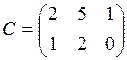
Решение:

Выполним указанные действия по шагам:

1) 

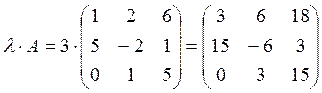
2) 

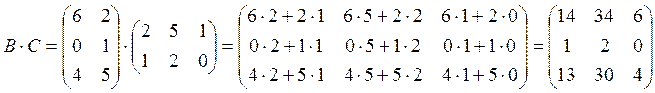
3) 

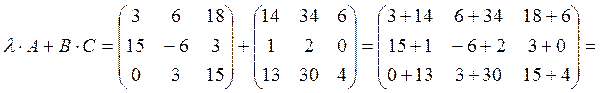
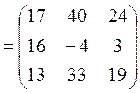
21.     Решить систему уравнений а)  используя формулы Крамера б)  матричным способом

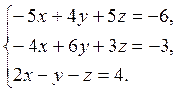
Решение:

а)  Решим систему с использованием формул Крамера

Вычислим главный определитель (определитель матрицы системы, составленной из коэффициентов при неизвестных):

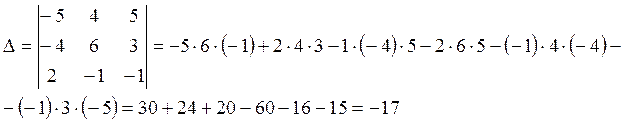
Поскольку , то для решения данной системы можно использовать формулы Крамера.

Вычислим побочные определители (которые получаются из главного при замене столбца коэффициентов при соответствующей переменной столбцом свободных членов):

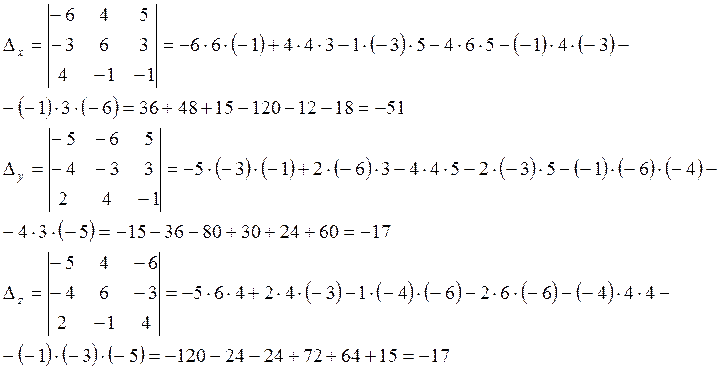
Тогда , , .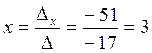

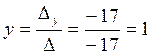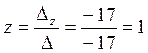Выполним проверку найденного решения. Для этого подставим полученные значения в исходную систему:

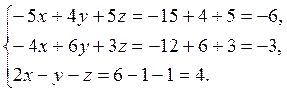
Поскольку при подстановке все уравнения обратились в тождества, то решение найдено верно.

б)  Решим систему матричным способом

Запишем систему в матричном виде , где

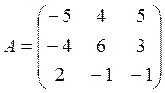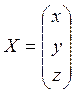 – матрица системы,  – вектор-столбец неизвестных,  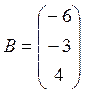– вектор-столбец свободных членов.

Тогда , т.е. для решения системы необходимо найти матрицу, обратную матрице  и умножить ее на столбец свободных членов.

Поскольку определитель матрицы системы отличен от нуля (), то обратная матрица существует. Найдем ее.

Транспонируем матрицу  (т.е. строки делаем столбцами, столбцы – строками):

.

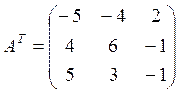Вычислим алгебраические дополнения элементов транспонированной матрицы:

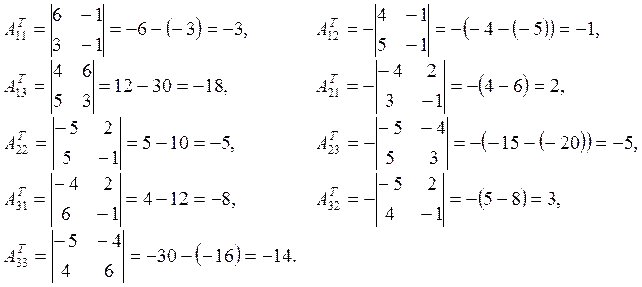
Запишем присоединенную матрицу:

.

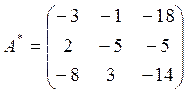Тогда

.

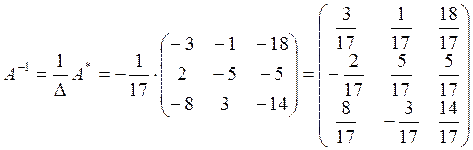Найдем решение системы:

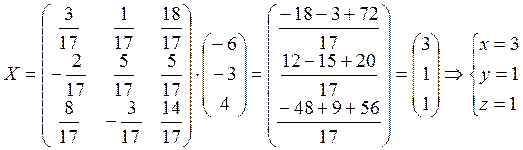
32.     Решить систему уравнений методом Гаусса.

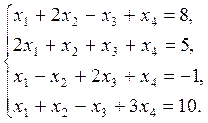
Решение:

Прямой ход метода Гаусса: запишем расширенную матрицу системы и путем эквивалентных преобразований приведем ее к трапецеидальному виду:

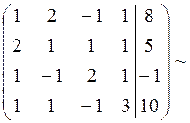
Элементы первой строки умножим на (-2) и прибавим их к соответствующим элементам второй строки. Из элементов третьей и четвертой строк вычтем соответствующие элементы первой строки:

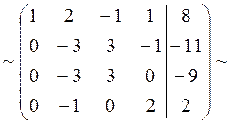
Поменяем местами вторую и третью сроки:

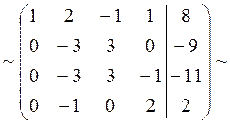
Элементы второй строки разделим на (-3):

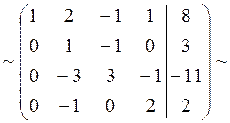
Элементы второй строки умножим на 3 и прибавим их к соответствующим элементам третьей строки. Элементы второй строки прибавим к соответствующим элементам четвертой строки:

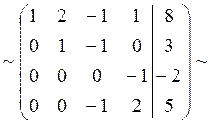
Поменяем местами третью и четвертую строки:

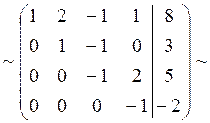
Элементы третьей и четвертой сток разделим на (-1):

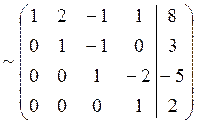
Обратный ход метода Гаусса: по полученной эквивалентной матрице восстановим и решим систему уравнений

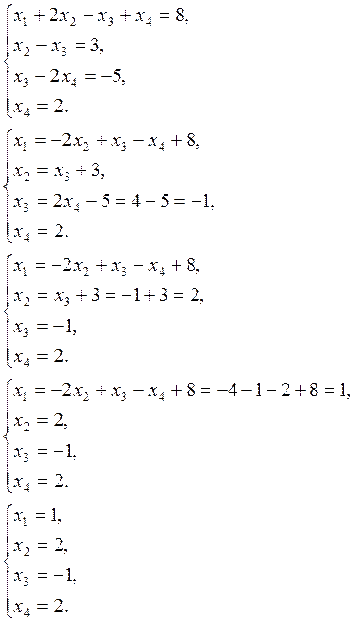
Выполним проверку найденного решения. Для этого подставим полученные значения в исходную систему:

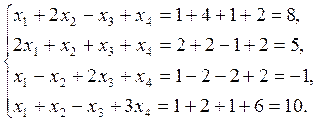
Поскольку при подстановке все уравнения обратились в тождества, то решение найдено верно.

41.     Выполнить действия в алгебраической форме. Результат записать в тригонометрической и показательной форах.

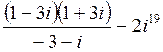
Решение:

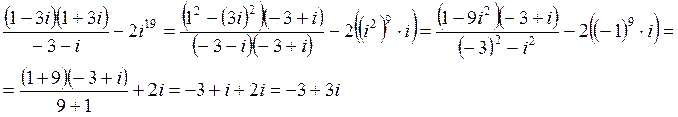
Запишем полученный результат в тригонометрической форме. Для этого найдем модуль комплексного числа и его главный аргумент.

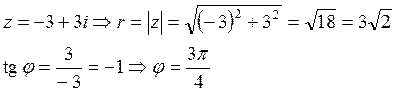
Тогда

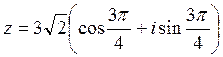 – тригонометрическая форма записи комплексного числа

 – показательная форма записи комплексного числа

КОНТРОЛЬНАЯ РАБОТА 2

1.       Доказать, что векторы , ,  образуют базис и найти координаты вектора  в этом базисе.

, , , .

Решение:

Составим и вычисли определитель из координат векторов , , :

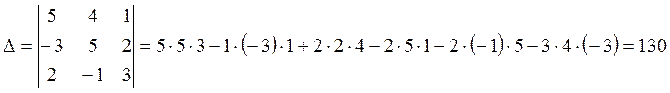
Поскольку , то векторы , ,  линейно независимы, т.е. образуют базис.

Запишем разложение вектора  по базису , , :

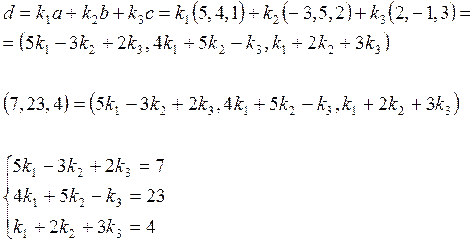
Решим полученную систему по формулам Крамера. Главный определитель вычислен выше: .

Вычислим побочные определители:

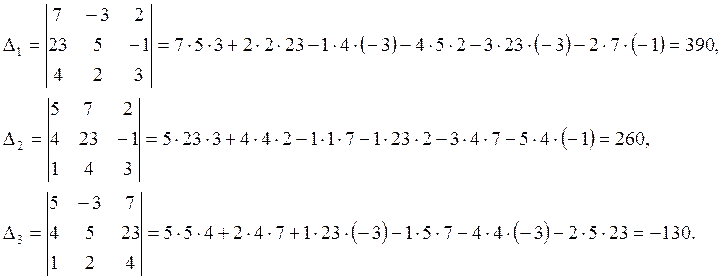
Тогда , , .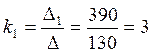

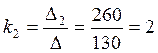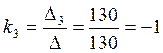Таким образом,

12.     По координатам точек ,  и  для указанных векторов найти:

а)  модуль вектора

б)  скалярное произведение векторов  и

в)  проекцию вектора  на вектор

г)  координаты точки , делящей отрезок  в отношении 2:3

, ,

Решение:

а)  Найдем координаты векторов  и :

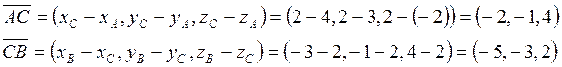
Найдем координаты вектора :

Находим его модуль:

б)  Найдем координаты вектора :

Находим скалярное произведение векторов  и :

в)  Вектор , .

Для нахождения проекции вектора  на вектор  воспользуемся формулой

.

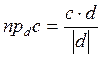Для этого вычислим скалярное произведение векторов  и  и модуль вектора :

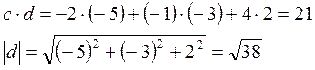
Тогда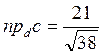

г)  Для нахождения координат точки , делящей отрезок  в отношении 2:3 воспользуемся формулами:

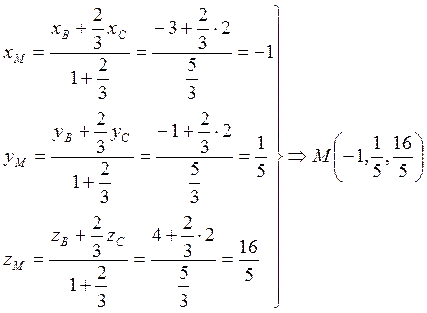
21.     Даны вершины треугольника , , . Найти:

а)  уравнение стороны ;

б)  уравнение высоты ;

в)  уравнение медианы ;

г)  точку  пересечения медианы  и высоты ;

д)  уравнение прямой, проходящей через вершину  параллельно стороне ;

е)  расстояние от точки  до прямой .

, ,

Решение:

а)  Найдем уравнение стороны  как уравнение прямой, проходящей через две заданные точки:

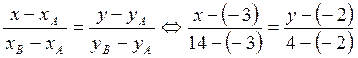
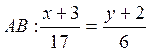 – каноническое уравнение стороны

б)  Найдем уравнение высоты . Поскольку  перпендикулярно , то вектор нормали к прямой  будет параллелен высоте , т.е. можно рассматривать его в качестве направляющего вектора для высоты .

Найдем вектор нормали к стороне , для этого преобразуем найденное в п. а) уравнение:

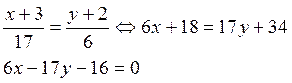
Тогда вектор нормали имеет координаты: .

Искомое уравнение высоты  напишем как уравнение прямой, проходящей через заданную точку параллельно заданному вектору:

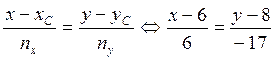
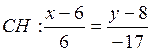 – каноническое уравнение высоты

в)  Найдем уравнение медианы . Поскольку точка  – середина противолежащей стороны , то найдем ее координаты по формулам: