Описание алгоритма. Постановка решения конкретного примера. Исходный код программы

ФЕДЕРАЛЬНОЕ АГЕНСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ МОРСКОГО И РЕЧНОГО ФЛОТА

ИМЕНИ АДМИРАЛА С.О. МАКАРОВА»

Факультет информационных технологий

Кафедра комплексного обеспечения информационной безопасности

АЛГОРИТМ ПОИСКа В ГЛУБИНУ

Выполнил:

студент ИП-21,

Проверил:

заведующий кафедрой, д.т.н., профессор

Санкт-Петербург

2015

Оглавление

Оглавление. 2

Описание алгоритма. 3

Постановка решения конкретного примера. 7

Исходный код программы.. 10

Скриншот выполнения программы.. 12

Описание алгоритма

Поиск в глубину (англ. Depth-first search, DFS) – рекурсивный алгоритм обхода вершин графа. Данный метод предполагает продвижение вглубь до тех пор, пока это возможно. Невозможность дальнейшего продвижения, означает, что следующим шагом будет переход на последнюю, имеющую несколько вариантов движения (один из которых исследован полностью), ранее посещенную вершину. Отсутствие последней свидетельствует об одной из двух возможных ситуаций: либо все вершины графа уже просмотрены, либо просмотрены все те, что доступны из вершины, взятой в качестве начальной, но не все (несвязные и ориентированные графы допускают последний вариант).

Пошагово алгоритм выглядит следующим образом:

1.  Берем некоторую вершину в качестве начальной. Помечаем каким-нибудь образом, что она является начальной вершиной.

2.  Идем по порядку в первую смежную с нею вершину. Отмечаем, что мы в ней были.

3.  Повторяем пункт 2 до тех пор, пока:

a.  Можем перейти в следующую смежную вершину, то есть, до тех пор, пока не дойдем до конца текущей ветви графа. В этом случае возвращаемся на предыдущую и выполняем пункт 3.b.

b.  Не дойдем до помеченной вершины. В этом случае:

  i.  Проверяем, можем ли мы перейти в следующую смежную НЕ помеченную вершину; если можем – повторяем пункт 2.

  ii.  Если же переход в следующую смежную НЕ помеченную вершину невозможен, то, в виду рекурсивности DFS, завершаем выполнение алгоритма для текущей вершины, после чего возвращаемся в предыдущую вершину и выполняем пункт 2.

c.  Не дойдем до вершины, помеченной как начальная. В этом случае смотрим можем ли мы пройти в другую непомеченную вершину. Если можем, то выполняем п.2; в противном случае граф (по крайней мере, связный) считается пройденным.

Рассмотрим действие этого алгоритма на простом примере.

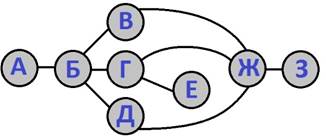
Обход будем совершать в порядке следования букв русского алфавита.

·  Начнем обход с вершины «А». Пометим её как начальную.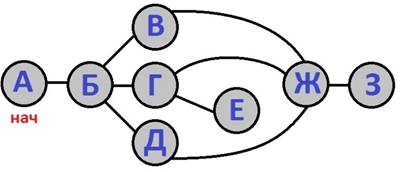

·  Следуя п.2, идем в вершину «Б». Пометим её.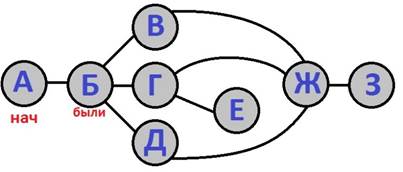

·  Следуя п.2, идем в вершину «В». Пометим её.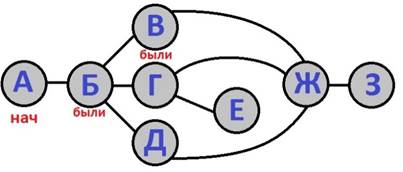

·  Следуя п.2, идем в вершину «Ж». Пометим её.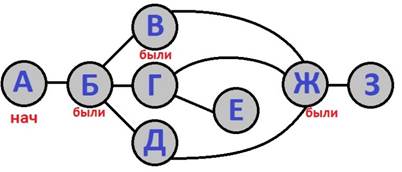

·  Следуя п.2, идем в вершину «З». Пометим её.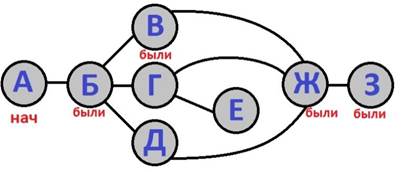

·  Из вершины «З» не попасть в непомеченную вершину. Следуем п.3. Возвращаемся в предыдущую и смотрим, куда мы можем попасть из вершины «Ж». В Данном случае мы можем пойти либо в вершину «Г», либо в вершину «Д». Так как мы следуем порядку следования букв в русском алфавите, то идем в вершину «Г», поскольку буква «г» идет раньше буквы «д» (хотя, в конкретно этом случае это не столь важно).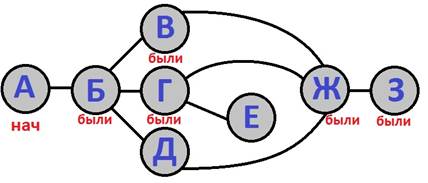

·  Следуя п.2, идем в вершину «Е». Пометим её.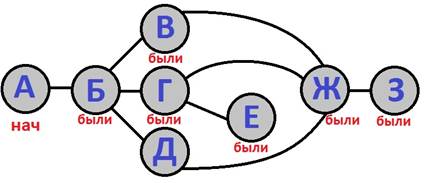

·  Из вершины «Е» не попасть в непомеченную вершину. Следуем п.3. Возвращаемся в предыдущую и смотрим, куда мы можем попасть из вершины «Г». В данном случае непомеченных смежных вершин вершине «Г» нет. Следуя п.3, возвращаемся в вершину «Ж». Из вершины «Ж» можем попасть в непомеченную вершину «Д». Следуя п.2, идем в вершину «Д». Пометим её.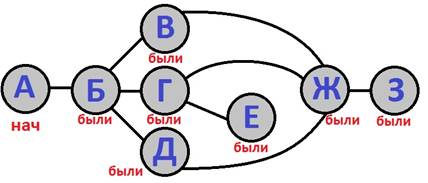

·  Из вершины «Д» не попасть в непомеченную вершину. Следуя п.3, мы сделаем серию следующих обратных переходов:

o  «Д» -> «Ж»

o  «Ж» -> «В»

o  «В» -> «Б»

o  «Б» -> «А»

·  Вершина «А» помечена как начальная. Из неё больше не ведут непомеченные вершины.

·  Конец.

Постановка решения конкретного примера

Постановка решения будет реализована в виде выполнения алгоритма вручную и программным образом.

В программе граф будет представлен в виде матрицы смежности.

Матрица смежности – квадратная матрица размерности n, где n – количество вершин графа. Матрица заполняется следующим образом:

·  Если возможно перейти из вершины «1» в вершину «2», то элемент матрицы «1»-ой строки и «2»-ого элемента будет равен единице.

·  Если переход невозможен, то элемент матрицы равен нулю.

·  Если индексы элемента равны, это значит, что мы рассматриваем возможность перейти из текущей вершины в саму себя. В таком случае, элемент матрицы будет равен нулю (исключение составляют петли, но в данной работе они не используются).