




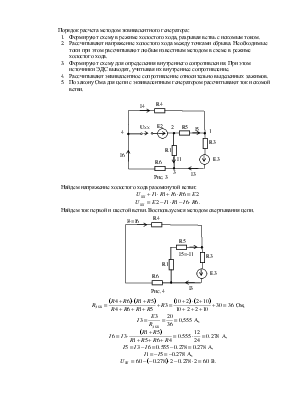














методе контурных токов уравнения составляют только по второму закону Кирхгофа для условных контурных токов. Количество контурных токов, как и количество уравнений должно быть равно числу независимых контуров рассматриваемой цепи.
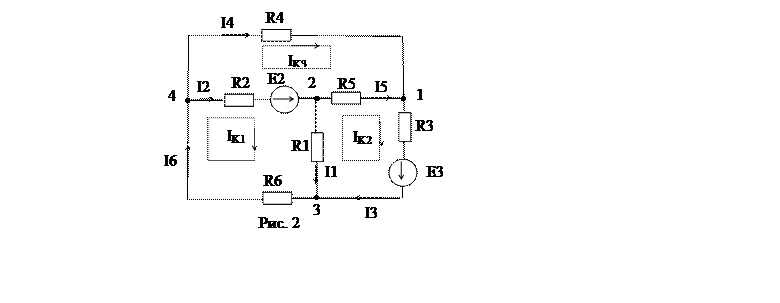
Порядок расчета методом контурных токов:
1. Произвольно задают УНП неизвестных реальных токов в ветвях цепи.
2. Произвольно задают УНП фиктивных контурных токов.
3. Составляют уравнения по второму закону Кирхгофа относительно контурных токов.
4. Решают эти уравнения.
5. Проверяют расчет.
Составим систему уравнений для данной электрической цепи:
![]()
![]()
![]() .
.
Подставим в систему значения сопротивлений и ЭДС:
![]()
![]()
![]() .
.
Решаем данную систему уравнений методом Крамера:
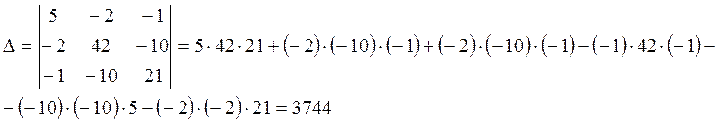
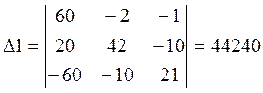
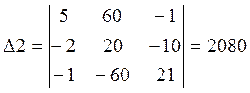
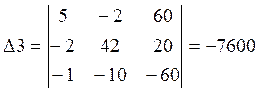
![]()
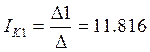 А;
А;
 А;
А;
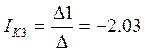 А.
А.
Выражаем реальные токи через известные контурные токи:
![]() А;
А;
![]() А;
А;
![]() А;
А;
![]() А;
А;
![]() А;
А;
![]() А.
А.
3. Сделать проверку по первому закону Кирхгофа.
Сделаем проверку по первому закону Кирхгофа:
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
Проверка по первому закону сошлась. Токи ветвей рассчитаны правильно.
4. Составить баланс мощностей.
Энергетический баланс мощностей составляют на основании закона сохранения энергии, согласно которому, энергия, выделившаяся в единицу времени в сопротивлениях схемы в виде тепла, должна быть равна энергии, вырабатываемой источниками за тот же промежуток времени.
![]() .
.
Найдем мощность, вырабатываемую источником:
![]() Вт.
Вт.
Найдем мощность, выделившуюся на нагрузке:
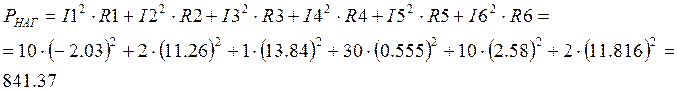
Найдем относительную погрешность нахождения баланса мощности:
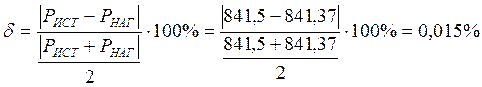
Погрешность нахождения баланса мощности получилась меньше 2%, что соответствует условию нахождения баланса мощности.
5. Рассчитать ток во второй ветви методом эквивалентного генератора.
В основе метода эквивалентного генератора лежит теорема об активном двухполюснике или об эквивалентном генераторе. Согласно этой теореме, сколь угодно сложную цепь относительно зажимов, выделенной ветви, можно представить активным двухполюсником или эквивалентным генератором. ЭДС этого генератора численно равна напряжению холостого хода на зажимах, выделенной ветви, а внутреннее сопротивление - эквивалентному сопротивлению цепи относительно тех же зажимов.
Порядок расчета методом эквивалентного генератора:
1. Формируют схему в режиме холостого хода, разрывая ветвь с искомым током.
2. Рассчитывают напряжение холостого хода между точками обрыва. Необходимые токи при этом рассчитывают любым известным методом в схеме в режиме холостого хода.
3. Формируют схему для определения внутреннего сопротивления. При этом источники ЭДС выводят, учитывая их внутреннее сопротивление.
4. Рассчитывают эквивалентное сопротивление относительно выделенных зажимов.
5. По закону Ома для цепи с эквивалентным генератором рассчитывают ток искомой ветви.
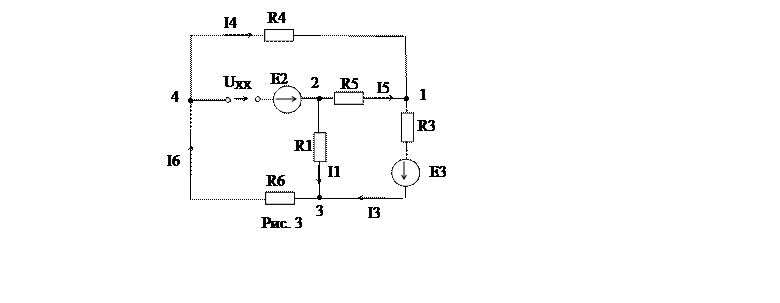
Найдем напряжение холостого хода разомкнутой ветви:
![]()
![]() .
.
Найдем ток первой и шестой ветви. Воспользуемся методом свертывания цепи.

 Ом,
Ом,
 А,
А,
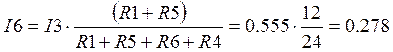 A,
A,
![]() A,
A,
![]() А,
А,
![]() B.
B.
Рассчитаем внутреннее сопротивление генератора. Для чего треугольник (рис. 5)
 R1-R5-R3
преобразуем в звезду. Получим схему рис. 6.
R1-R5-R3
преобразуем в звезду. Получим схему рис. 6.

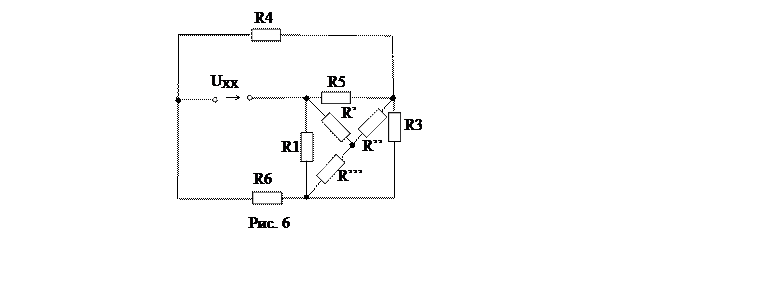
 Ом,
Ом,
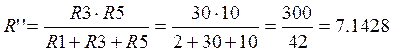 Ом,
Ом,
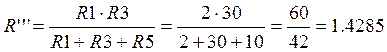 Ом.
Ом.
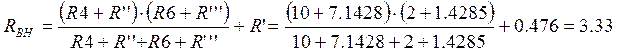 Ом.
Ом.
По закону Ома найдем ток ветви:
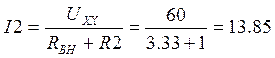 А.
А.
Ток второй ветви, найденный по методу эквивалентного генератора, равняется току второй ветви, найденному по методу контурных токов. Следовательно, расчет методом эквивалентного генератора выполнен, верно.
6. Построить потенциальную диаграмму для любого контура.
Потенциальная диаграмма – это график изменения потенциала вдоль замкнутого контура или участка цепи. Построим потенциальную диаграмму для контура a-b-c-d. Заземлим одну из точек или узлов заданного контура. При этом полагают, что потенциал этой точки равен нулю.
Пусть ![]() , тогда
, тогда
![]() В,
В,
![]() В,
В,
![]() В,
В,
![]() В.
В.
Рассчитаем суммарное сопротивление контура:
![]() Ом.
Ом.
Построим потенциальную диаграмму.
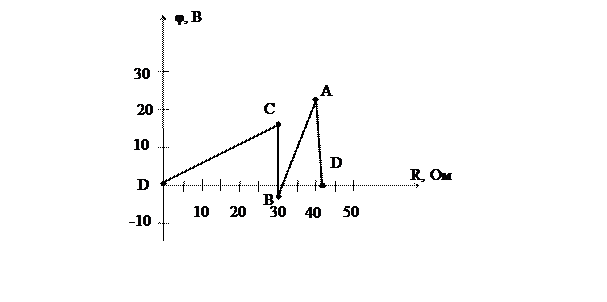
Рис. 7
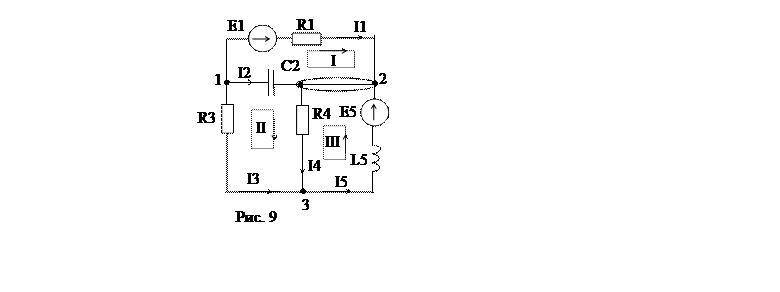
2.2. Расчет электрической цепи переменного тока.
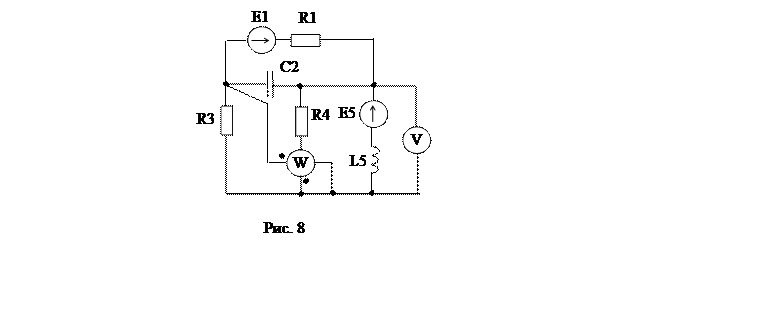
Исходные данные:
R1=10 Ом; C2=127 мкФ; R3=40 Ом; R4=50 Ом; L5=0.143 Гн,
![]() В,
В, ![]() В.
В.
1. Составить систему уравнений по законам Кирхгофа в дифференциальной и комплексной формах (решать систему не надо).
Порядок составления полной системы уравнений по законам Кирхгофа:
1. Произвольно задают УНП неизвестных реальных токов в ветвях цепи.
2. Записывают по законам Кирхгофа систему линейных алгебраических уравнений относительно неизвестных токов.
Дифференциальная форма законов Кирхгофа:
1: ![]() ,
,
2: ![]() ,
,
I: 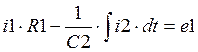 ,
,
II: 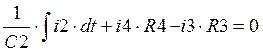 ,
,
III: 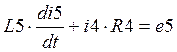 .
.
Законы Кирхгофа в комплексной форме:
1: ![]() ,
,
2: ![]() ,
,
I:
![]() ,
,
II: ![]() ,
,
III: ![]() .
.
2. Составить систему уравнений по методу узловых потенциалов. Решить систему, определить потенциалы узлов и токи ветвей.
Порядок расчета методом узловых потенциалов:
Найдем полные сопротивления ветвей:
![]() Ом,
Ом,
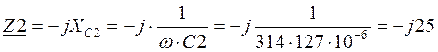 Ом,
Ом,
![]() Ом,
Ом,
![]() Ом,
Ом,
![]() Ом.
Ом.
Заземлим 3 узел, полагая потенциал этого узла равным нулю:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.