Определим эквивалентный момент по формуле:
Мэкв = (М2сум + М2к)1/2.
Для сечения 4 Мэкв = (3,452 + 1,842)1/2 = 3,91 кН·м.
Из условия прочности |σ| > σэкв = Мэкв / W, учитывая, что
W = π·d3 / 32, d ≥( Mэкв ·32 / |σ|·π)1/3 = (3910 · 32 / 259 · 106 · π)1/3 = 0,0536 м = 53,6мм.
3.5.2 Коренная шейка
Для коренной шейки вала опасным является сечение 6 согласно третьей теории прочности. Мэкв = (2,562 + 2,022)1/2 = 3,26 кН·м.
Воспользовавшись формулой, получим d ≥ ((3260·32):(259·106· π))1/3 =
= 0,0504 м = 50,4м.
Как видно из полученных значений диаметров шеек можно принять одинаковый диаметр d = 55 мм для коренной и шатунной шеек.
3.5.3 Щека
Поперечное сечение щеки вала определяем по конструктивным соображениям. Рекомендуемая толщина щеки δ = (0,45… 0,85) d.
Принимая среднее значение коэффициента, получим δ = 0,58 · 55 = 32 мм. Принимаем δ = 32 мм. Ширину шейки возьмем в 2 раза больше: h = 2δ = 2·34 = = 64 мм.
Осуществим проверку прочности принятых размеров щеки вала. В наиболее неблагоприятных условиях находится правая щека вала – участок
5 – 6 . Необходимо рассмотреть наиболее напряженные точки A, B и С сечения щеки.
Напряжение в характерных точках сечения определим по формуле сложного сопротивления
σ = ± N / F ± My / Wy ± Mz / Wz.
Определим геометрические характеристики сечения:
F = δh = 0,032 · 0,064 = 2,0 · 10-3 м2;
Wy = δh2/6 = 0,032 · 0,064 / 6 = 2,18 · 10-5 м3;
Wz = hδ2/6 = 0,064 · 0,0322 / 6 = 1,09 · 10-5 м3.
Из эпюр имеем : Мк = 1,07 кН · м;
Мy = 0,9 кН · м;
Мz = 2,33 кН · м;
N = - Q1y – Ay = 3,55 - 4,23 = - 0,68 кН · м,
где знак минус означает, что щека подвергается сжатию осевой силой N. Используя формулу, для точки A, поучим
σA = - N / F – Мy /Wy – Mz / Wz = - 680 : (2,0 · 10-3) – 900 : (2,18 · 10-5) –
– 2330 : (1,09 · 10-5) = - 172,14 МПа.
Определим нормальное напряжение в точки В
σВ = - N / F– Mz / Wz= - 680 : (2,0 · 10-3) – 2330 : (1,09 · 10-5) = 214,1 МПа
Касательные напряжения для точки B найдем для прямоугольного сечения по формуле
τ = Мк / Wt,
где Wt = αhδ2 – условный полярный момент;
α – коэффициент, зависящий от соотношения h / δ.
При h / δ = 2, α = 0,246. Тогда
Wt = 0,246 · 0,064 ·0,0322 = 1,6 · 10-5 м3;
τB = Мк / Wt = 1070 : (1,6 · 10-5) = 66,88 МПа.
Эквивалентное напряжение в точке B согласно третьей теории прочности
σэкв В = (σ2В + 4τ2B)1/2 = (214,12 + 4 · 66,882)1/2 = 252 МПа < 259 МПа.
Таким образом, имеем недонапряжение менее 5% , что приемлемо.
Определим нормальное напряжение в точке С (рис.2.5), используя выражение
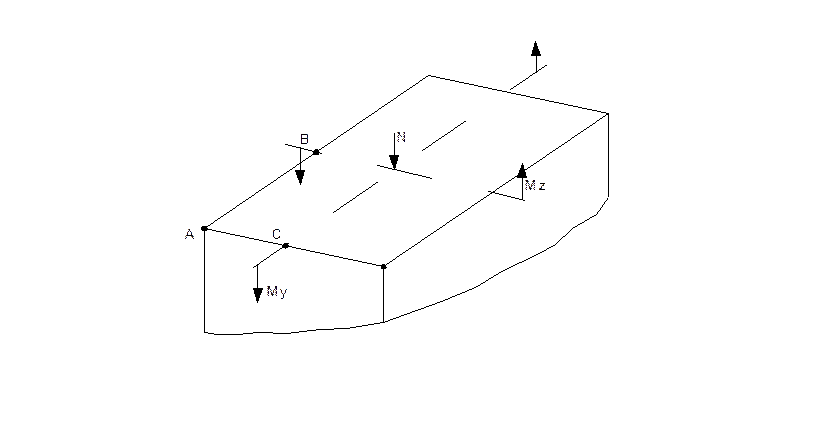Рисунок 2.5 –
К расчету щеки вала
σС = - N / F – My / Wy = - 680 : (2,0 · 10-3) – 900 : (2,18 · 10-5) =
= - 42 МПа.
Касательное напряжение получим по формуле τС = γ τB, где γ – коэффициент, который при h / δ = 2 равен γ = 0,796. Тогда τС = 0,796 ·66,88 = 53,2 МПа.
Эквивалентное напряжение в точке С
σэкв с = (σ2с + 4τ2с)1/2 = (- 422 + 4 · 53,22)1/2 = 114,4 МПа < 259 МПа.
Принятые размеры щеки 32 × 64 мм, как показывает расчет, удовлетворяет условиям прочности.
4 Надежность коленчатого вала по отдельным критериям
4.1 Оценка надежности коленчатого вала по критериям сопротивления усталости
Учитывая, что шатунная шейка вала находится в наиболее тяжелых условиях работы, произведем оценку ее надежности.
4.1.1 Оценка параметров распределения главных напряжений
Определим напряжения от суммарного изгибающего и крутящего моментов:
σ = М / W = М / (d3·π / 32) = 3450 / (0,0553·π / 32) = 211 МПа;
τ = М / Wρ = Мк / (2W) = Мк / (d3· π / 16) = 1840 / (0,0553· π / 16) = 56 МПа.
Определим главные напряжения по известной формуле:
σ5-6 = (1/2) [σ ± (σ2 + 4τ2)1/2].
Следовательно, σ5 = (1/2) [211 + (2112 + 4·562)1/2] = 225 МПа;
σ6 = (1/2) [211 - (2112 + 4·562)1/2] = -14 МПа.
Учитывая, что σ6 « [σ], можно считать, что шатунная
шейка вала работает в условиях линейного напряжения (ЛНС) при σ1 = 
= 225 МПа. Будем считать
это значение средним, т.е. = 225
МПа
Принимаем коэффициент вариации главного напряжения υσ =
0,05, найдем его квадратическое отклонение: Sσ = υσ=
0,05· 225 = 11,25 МПа.
4.1.2 Оценка параметров распределения предела выносливости шейки вала
Для стали 18ХГТ найдем среднее значение предела выносливости по результатам испытаний образцов диаметром d = 10 м: σ-1d = 235МПа.
Оценку параметров функции распределения предела выносливости шейки вала с диаметром D > d произведем по следующей методике.
Будем строить функцию распределения пределов выносливости P(σ-1d) образцов диаметром d = 10 мм по двум точкам, полагая, что распределение σ-1 подчиняется нормальному закону. В качестве первой точки
А (рис.3.1) выбираем среднее значение предела выносливости 
= 235 МПа, которое соответствует
вероятности Р = 0,5. В качестве второй точки В принимаем минимальное σ-1min значение пределов выносливости, которое определяют из
соотношения
σ-1min = 0,5·235 = 117,5 МПа.
Оно соответствует вероятности Р = 0,001. Таким образом, точка В имеет координаты (117,5;0,001) (рис.3.1).
Построим теперь функцию распределения пределов выносливости P(σ-1d) шейки коленчатого вала диаметром D = 55 мм. Чтобы иметь
масштабный эффект, используем экспериментально установленный факт, согласно
которому функции распределения пределов выносливости образцов различных
диаметров имеют общую нижнюю границу рассеяния σ-1min (точка В). теперь следует найти среднее
значение предела выносливости шейки вала, используя ту или иную теорию
масштабного эффекта в сопротивлении усталости. Наиболее простую оценку 
получаем по формуле = Кd. где Кd – масштабный коэффициент.
Рис.3.1. К оценке параметров функции распределения пределов выносливости шатунной шейки шейки вала
Для D = 65 мм имеем Кd = 1 – 0,243·(lgD – lg10) = 0,82. Тогда =
0,8·235 =193 МПа.
Тем самым получим точку С для функции распределения пределов выносливости шейки вала (рис.3.1). Изобразим функции P(σ-1d) и P(σ-1D). Среднеквадратическое отклонение пределов выносливости Sσ-1D вычислим по формуле
Sσ-1D = ( - σ-1min) / 3,09 = (193 – 117,5) / 3,09 = 24,43
МПа, где квантиль нормального распределения Zp = 3.09 соответствует вероятности Р =
0,001.
Таким образом, для шатунной шейки вала найдены следующие параметры функции распределения пределов выносливости:
= 193 МПа;
Sσ-1D = 24 МПа.
4.1.3 Расчет вероятности усталостного разрушения шатунной шейки
Вероятность разрушения вала при ЛНС рассчитывают по формуле
Р = 1 – Ф [ - (
- ) / (S2σ + S2σ – 1)1/2],
где Ф(х) – табулированная функция Лапласа. Подставляя в эту формулу найденные параметры, получим
Р = 1 – Ф [ - (193 – 225) / (24,432 + 11,252)1/2] = 1 – Ф (1,19) = 1 – 0,883 = 0,117
Это означает, что за период эксплуатации, соответствующий базе, на который определено значение предела выносливости вала, из одной сотни коленчатых валов ожидается усталостное разрушение одного-двух валов.
4.1.4 Оценка надежности шатунной шейки вала по коэффициенту запаса прочности
Вероятностный коэффициент запаса прочности при ЛНС вычислим по формуле
=
/ 
= 193 / 225 = 0,86.
Для того, чтобы определить, будет ли иметь место разрушение вала, найдем критический коэффициент запаса прочности
nk = [1 + t(ασ, γσ) υσ] / [1 – t(ασ - 1,γσ - 1)(Sσ-1 / σ-1)],
где t(α, γ) = Z(1 – α) [1 + Zγ / (2n0)1/2 + (5 Zγ2 + 10) / 12n0].
Здесь Zγ, Z(1 – α) – квантили нормального распределения, соответсвующие доверительным вероятностям γ и (1 – α); α – коэффициент значимости; n0 – число испытаний, по которому установлены параметры распределения предела выносливости вала. Для нашего случая принимаем: γ = 0,99; α = 0,001; следовательно , (1 – α) = 0,999; n0 = 300.
Тогда по таблице квантилей находим Zγ = 2,33; Z(1 – α) = 3,09.
Толерантный коэффициент вычисляем по формуле
t(α, γ) = 3,09 [1 +2,33 / (2·300)1/2 + (5·2,332 + 10) / (12·300)] = 3,42.
Находим значение nk = [ 1 +3,42·0,05] / [1 – 3,42 · 24,43 / 193] = 2,06.
Сравнивая значения nk и 
, устанавливаем, что nk > .
Это означает, что существует некоторая вероятность Р разрушения вала, которую
оценивают по формуле
np = [1 + (1 – [1 – (k / рf)υ2σ-1] [1 - (k / рf)υ2σ)1/2] / [1 - (k / рf)υ2σ-1],
где k и f – коэффициенты, известные априори.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.