1. Исходные данные
Расчету подлежит простой коленчатый вал, лежащий на двух опорах (рис. 1.1).
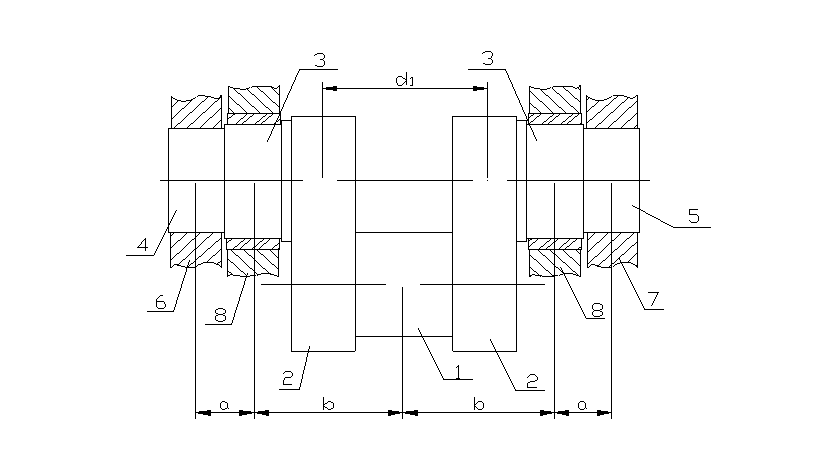Рисунок 1.1–Схема
простого коленчатого вала
Обозначения:
1 – шатунная шейка;
2 – две щеки;
3 – две коренных шейки;
4 и 5 – цапфа;
6 – шкив;
7 – маховик;
8 – подшипники.
На вал действуют нагрузки (рис. 1.2).
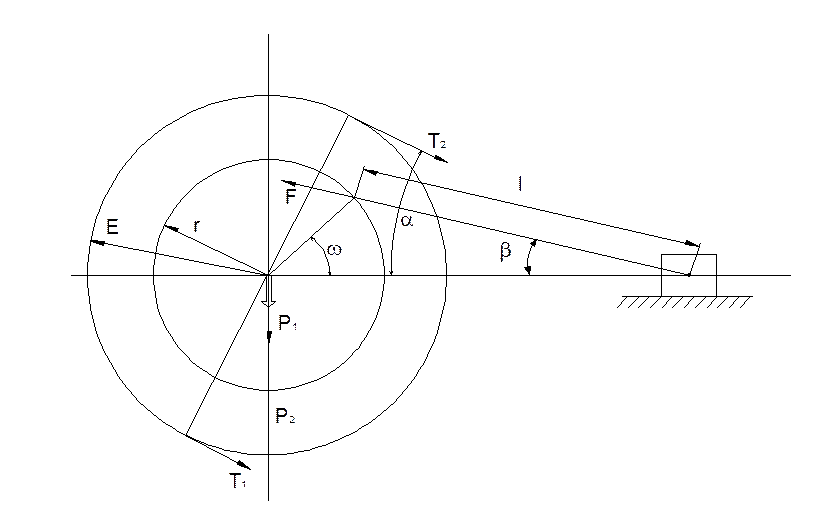
Рисунок 1.2–Нагрузки действующие на вал
Обозначения:
Р1 и Р2 – вес шкива и маховика соответственно;
F – сила , действующая на шатунную шейку со стороны поршня ;
Т1 и Т2 – натяжения соответственно сбегающей и набегающей ветвей ременной
передачи, посредством которой крутящий момент передастся
исполнительному механизму.
Коленчатый вал двигателя передает мощность N = 200 л.с. при п = 1500 об/мин через ременную передачу. Вал имеет одно колено с плечом кривошипа r = 160 мм; заданы размеры (см. рис.1.1): а = 180 мм; b = 170 мм; с = 150 мм и d1= 90 мм. На одном конце вала посажен шкив массой m1= 380 кг, а на другом - маховик массой m2 = 1100 кг. Шкив передает мощность через ременную передачу под углом α = 500 к горизонту. Натяжение набегающей ветви примем равно двойному натяжению сбегающей ветви. Радиус шкива Rш = 450 мм. Наибольшая нагрузка на нал будет при угле наклона кривошипа к горизонту φ= 41°. Отношение длины шатуна к длине плеча кривошипа l/r = 4,7. Материал вала – сталь 40. Коэффициент запаса к=1,45.
Вычислим мощность:
N = 736∙N (л.с) (1)
N = 736∙200 = 1,47∙105 Вт.
Найдем угловую скорость вращения вала двигателя:
ω= πn / 30 (2)
ω= (π∙1500) : 30 = 157 с-1,
где п - частота вращения , об/мин.
Определим массовые силы по формуле
Р = mg , (3)
где g - ускорение свободного падения. Тогда
P1 = m1g (4)
P1= 380∙9,81 = 3728 Н = 3,73 кН;
Р2 = m2g (5)
P2= 1100∙9,81 = 10791 Н = 10,8 кН.
Линейные размеры вала: г = 160 мм = 0,16 м; а=180 мм = 0,18 м; b=170 мм = 0,17м; с = 150 мм = 0,15 м; d1 = 90 мм = 0,09 м ; R = 450 мм = 0,45 м.
2. Определение расчетных нагрузок на вал
Крутящий момент, возникающий на валу двигателя:
Мк = N / ω, (6)
Mk= 1,47∙105 : 157 = 0,9 кН∙м.
Натяжение сбегающей ветви ременной передачи находим по крутящему моменту
Т1= Мк / R ш , (7)
Т1 = 0,9·103 : 0,45 = 2кН.
Натяжение набегающей ветви Т2 = 2T1 = 2∙2= 4кН.
Со стороны шкива под углом α = 50° к горизонту на вал действует изгибающая сила (рис.1.3) Т = Т1 + Т2 = 2 + 4= 6 кН.
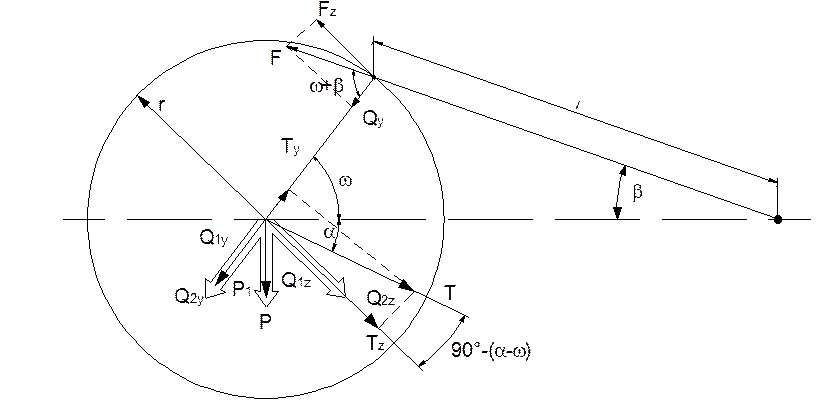
Рисунок 1.3 – Разложение сил на составляющие по двум направлениям
Кроме того, здесь действует вертикальная изгибающая сила от веса шкива
Р1=3,73 кН. На противоположном конце вала действует вертикальная изгибающая сила от веса маховика Р2 = 10,8 кН.
Определим окружную силу :
Fz = Мк / r , (8)
Fz = 0,9∙103 : 0,16 = 6 кН.
Определим угол β
sin β = 1/r∙sin φ=1/4,7∙ sin 41°= 0,1396, β=8°01' (10)
Определим радиальную силу
Qу = Fz ctg ( φ + β), (11)
Qу = 6· ctg (41°+8°01') = 5,21 кН.
Силы, действующие в плоскости кривошипа:
– на левом конце вала
Q1y = Р1 sin φ–Т cos ( α + φ) = 3,73 sin 41° –6 cos 91° = – 3,55 кН
– на правом
конце вала 
Q2y = Р2 sin φ = 10,8 sin 41° = 7,08 кН.
Рисуем схему систем сил плоскости колена (1.4) и плоскости, перпендикулярной колену (рис. 1.5).
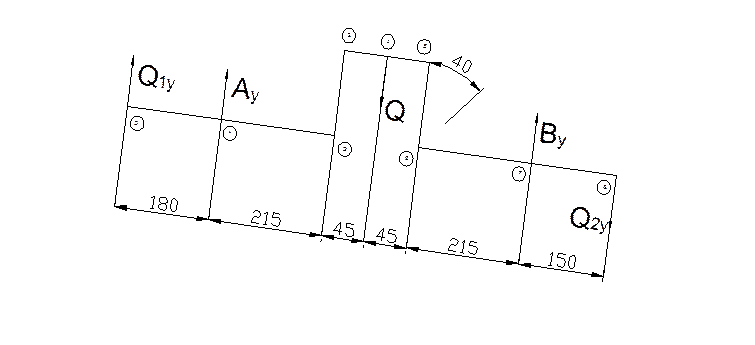
Рисунок 1.4 – Система сил в плоскости колена.
Найдем реакции опор Aу и Bу , действующие перпендикулярно плоскости кривошипа (рис. 1.4), используя уравнения моментов относительно этих точек:
Σ MВj = 0 ; 0,26∙Qy−Q2y∙0,15 – Ay∙0,52−Q1y∙0,70=0; (12)
Ay=4,23 кН ;
Σ МАi = 0; 0,52∙By −Q1y∙0,18−Qy∙0,26−Q2y∙0,67=0 (13)
Bу = 12,95 кН.
Σ Yi = 0 ; Qу + Q2у –Bу+Aу–Q1у = 0;
5,21+7,08–12,95+4,23–3,55=0.
Правильность решения уравнений (12) и (13)
проверим, используя условие равновесия: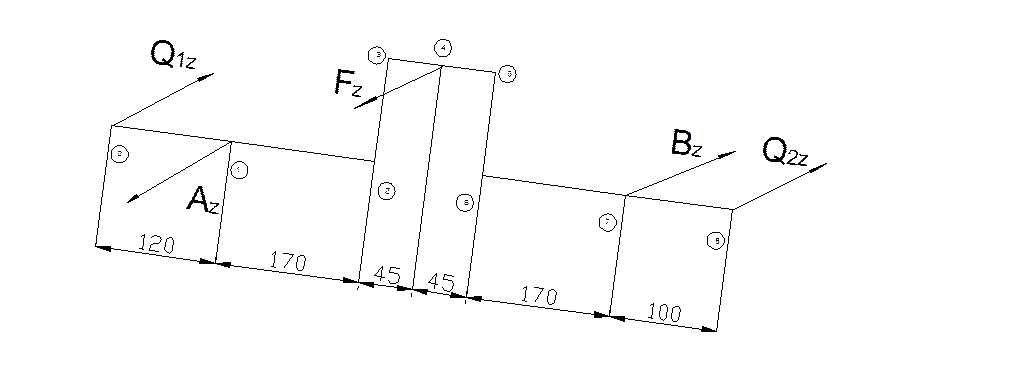 
Рисунок1.5 Система
сил в плоскости, перпендикулярной колену
Сила, действующая перпендикулярно к плоскости кривошипа:
– на левом конце вала:
Q1z = Р1 cos φ+ Tsin ( α + φ) = 3,73 cos 41o + 6sin 91° = 8,81 кН;
– на правом конце вала:
Q 2z = Р2 сos φ = 10,8 cos 41° = 8,15 кН.
Найдем реакции опор Аz и Bz, используя уравнения моментов относительно этих точек:
ΣMA=0;0,18Qlz+ 0,26 Fz + 0,52 Вz – 0,67 Q2z = 0; (14)
Bz = ( 0,67·8,15–0,18·8,81–0,26·6 ) : 0,52 = 4,45 кН;
ΣМв=0;0,70Q1z – 0,52Az – 0,26 Fz –0,15 Q2z = 0; (15)
Az = (0,70·8,81–0,26·6–0,15·8,15 ) : 0,52 =6,51 кН.
Правильность решения уравнений (14) и (15) проверим, используя условие равновесия:
Σ Zi = О : Fz + Bz –Аz – Q2Z –Qlz = 0 ;
6 + 4,45 + 6,51 –8,15 –8,81 = 0.
3 Построение эпюров изгибающих моментов
3.1 Изгибающие моменты Mz
Для построения эпюры изгибающих моментов определим ординаты эпюр моментов в характерных сечениях (рис. 1.6):
М0=М8 = 0;
М1= 0,18∙Q1y = 0,18∙3,55 = 0,64 кН.м;
М2 = М3 = Q1y∙0,395+Ay∙0,22= 3,55∙0,395+4,23∙0,22 = 2,33 кН.м :
М4 = Q1y∙0,44+Ay∙0,26 = 3,55∙0,44 + 4,23∙0,26 = 2,66 кН.м :
М5 = М6 = Q1y∙0,485+Ay∙0,31-Qy∙0,045 = 3,55∙0,38+4,23∙0,26 –5,21∙0,045 = 2,22кН.м ;
М7 = -Q2y∙0,15 = -7,08∙0,15 = – 1,06кН.м.
По полученным значениям строим эпюру моментов Mz
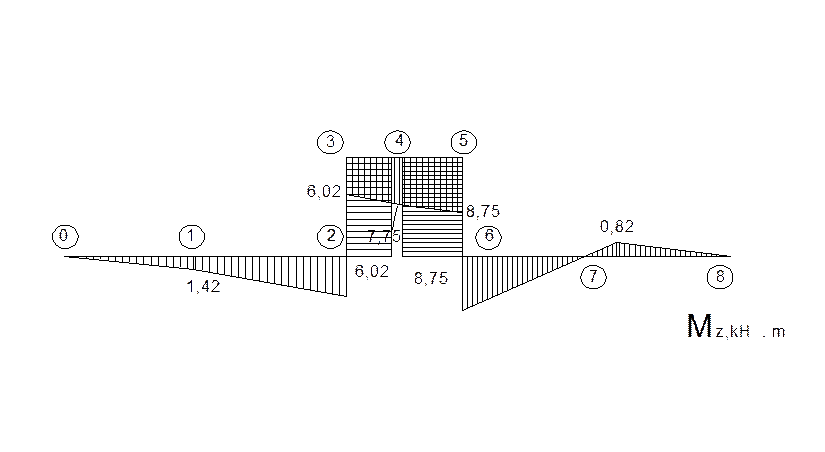
3.2. Изгибающие моменты My
Ординаты эпюр моментов в характерных сечениях
М0 = М8 = 0;
М1 = Q1z·0,18=8,81·0,18=1,59кН.м;
Вал: М2 = Q1z·0,395 - Az·0,215=8,81·0,395 – 6,51·0,215=2,08кН.м ;
Щека: М2 = - Мк = - 0, 9кН-м ,
Вал: М3 = М2 = 2,08кН.м ;
Щека: М3 = - Мк + Q1z·0,17 - Az·0,17= -0,9 + (8,81 – 6,51) 0,16 =- 0,53кН.м ;
Вал: М4 = Q1z·0,44 - Az·0,26 = 8,81 0,44 – 6,51 0,26 =2,19кН.м ;
М5 = М6 = Q2z·0,275 - Bz·0,215 = 8,15·0,275 – 4,45·0,215=1,28кН.м ;
Щека: М5 =Q2z·0,16 - Bz·0,16 = 8,15·0,16 – 4,45·0,16=0,59кН.м;
М7= Q2z·0,15=8,15·0,15=1,22кН.м.
По полученным значениям строим эпюру моментов My
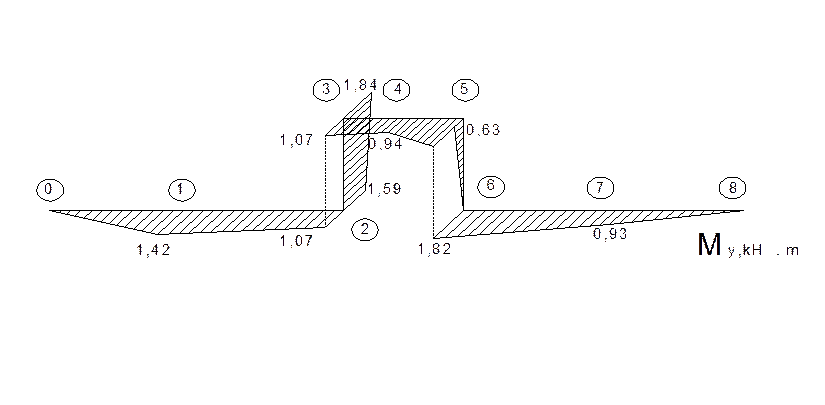
3.3. Суммарные изгибающие моменты Мсум
Суммарные моменты определяем в характерных точках для элементов круглого поперечного сечения (шейки и цапф вала) по формуле
Мсум = 
Получаем:
М1сум = 
=
= 1,71 кН.м;
М2сум = М3сум,
= 
=
=
3,12 кН.м ;
М4сум = 
= 
=
3,45 кН.м ;
М5сум = М6сум
= 
= 
=2,56
кН.м ;
М7сум = 
=
=
1,62 кН.м;
М8сум = М0сум=0 кН.м;
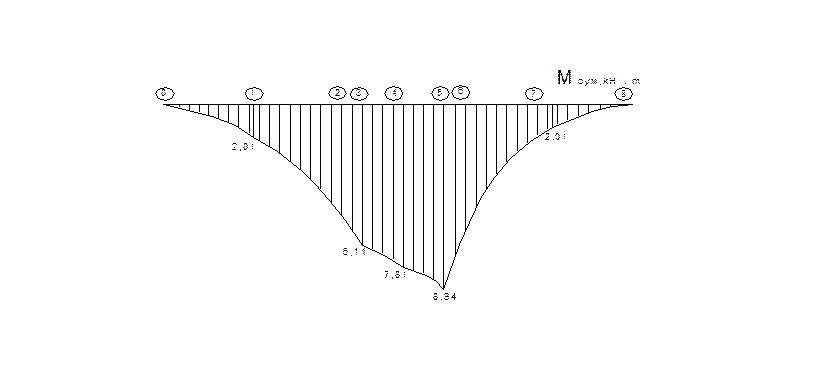
3.4. Крутящие моменты Мк
Используя (рисунок 1.) построим эпюры крутящих моментов. Ординаты этой эпюры в характерных сечениях будут:
М0 = М1 = М2 = Мк = 0, 9 кН.м ;
М23 = Q1z·0,395 - Az·0,215= 1,07 кН.м ;
М35 = Mk+Az·0,16 – Q1z·0,16 = 0,9+6,51·0,16 – 8,81·0,16=1,84 кН.м ;
М56 = Az·0,305 – Q1z·0,485+Fz·0,045= 6,51·0,305 – 8,81·0,485+0,045·6,00=2,02 кН.м ;
М7 = М8 = 0.
По полученным значениям строим эпюру крутящих моментов
.
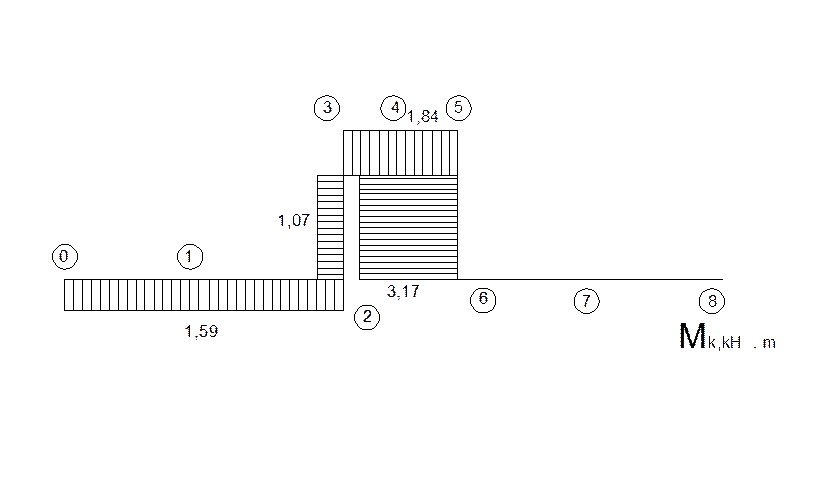3.5 Подбор размеров поперечных сечений
3.5.1 Шатунная шейка
Для шатунной шейки, как видно из построенных эпюр суммарных изгибающих Mсум и крутящих Мк моментов, опасным является сечение 4. Согласно исходным данным для стали 40 σт = 375МПа; к = 1,45. Тогда допустимое напряжение |σ| = σт / к = 375 / 1,45 = 259 МПа.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
