Метод утрированного плана - применение различных масштабов для наглядности и возможности графоаналитического проектирования плана

Метод утрированного плана

Сущность метода утрированного плана

для наглядности и возможности графоаналитического проектирования плана целесообразно применение различных масштабов: более мелкого для измерения расстояний и более крупного - для измеpения сдвижек. Для этогo и применяется метод утрированного плана.

Сущность метода заключается в следующем

 

 

КПК

 

IцIK

нIК

 

 

~ график

~

НормаЛей~

^F

I II"                                                   ()                                                 kK_/,

I?L1~                                      Г~,,._г

Для некоторой расстроенной кривой меюдом угловых диаграмм подбирается                                                                                                                           _у

кривая радиуса р и вычисляются сдвиги Лр между расстроенной кривой и кри­вой радиусa p. Дaлее предполагается, что запроектированная вместе c переход­ными кривыми кривая радиуса R соответствует проектным требованиям по величине и направлению сдвигов. Окончательные сдвиги глежху расстроенной кривой и кривой ра1ниуса R c учетом усгройсгва персходной кpивoй определя­ются по формуле

А=пр-N,

где N- нормаа1ь, г. е. расстояние:

- между т<риво радиуса р и касательными на участках НК_р - НПК, и НПК_г -

КК_р (1);

64

- между кривой радиуса р и кривой радиуса R- на участке КПК, - КПК_г (2); - между кривой радиуса р и переходными кривыми - на участках ННК, -

КПК,, НПК_г - КПК_г (3).

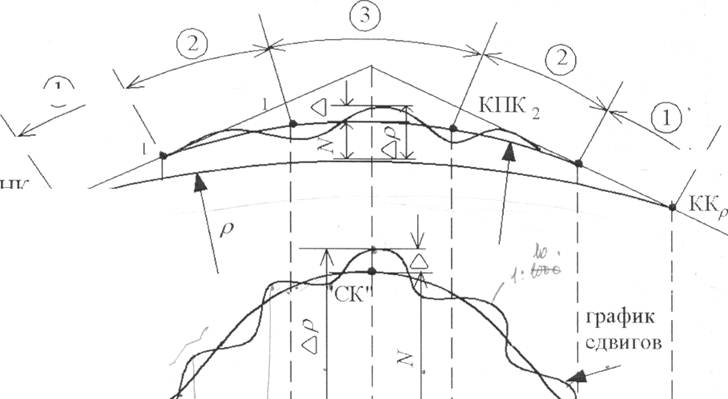
Графическое определение сдвигов 4 негюсредственно по плану в обычной системе координат не может быть осуществлено. Поэтому реальпый план заме­няется его моделью - утрированным планом. Для построения утриронанного плана вводится специальная система координат. Для этого кривая радиуса р разворачивается н нрямую и ггринимается за ось абсцисс (или ОСЬ р). Начало координат совмеiцается с серединой кривой радиуса р. На оси р откладываются длины кривых К, по оси ординат - сдвиги 4р и нормали N. Если сдвиги и нор­мали расположены снаружи кривой рациуса р, то они считаются положитель­ными и откладываются на утрированном плаiге вверк от оси р и наоборот. Это правило знаков согласуется с правилом знаков метода угловых диаграмм.

Далее, на оси р наносятся точки делеиия кривой. F3 точках деления кривой откладываются в виде ординат величины 4р и дэiя наглядности соединяются ломанной линией. Эта линиsг называется «графиком едвигоВ». В тех же точках деления кривой i-ia оси р отклады ваются в виде ординат величины N, получен­ная линия называется «графиком нормалей». Совмещенные графики сдвигов и нормалей называrотся «угрированным п.ланом» (УП).

«УП» лредставляет собой своеобразкую модель плана кривой в новой систе­ме координат. Мс>кду оригинальным планом и отображением «УП» сущесгвует однозначное соответствие. Отображением кривой радиуса р является ось абе­цисс; отображением г сущесгвуюн~ей кривой - график сдвигов; отображением проектной кривой - график нормалсй. На «YII» окончательныс сдвиги 4 опре­деляiотся графически как разность ординат rрафика сдвигов 4р и графика нор­малей, цто соответсгвует ньнiiеприведei-lной формуле.

Оиределение нормалеЙ и посТроеНие их гРафика

В метоце «УП» в качесгве нормали между двумя кривыми принимается отре­зок, равный разносги эвольвент дуг кривьlх равной длины. Величины нормалей Nопределяются различно в зависимости от зоны.

65

1 Оnределение нормалей между кривой радиуса р и касательны,ми - зона (1). В

ОСЬ р

В точках Нк~~и кК_р нормаль N= 0. 1{а « УП» эти точки растlоложеньl на оси р на расстоянии К,/2 тзправо и влево от начала коорцинат (точки « СК» ). Длпi-iа кривой радиуса ~

19=

ра_рдд.

В соответствии с принятьlм раныilе допущением о равенстве нормали N эвольвенте ab дуги ad уравнение нормали между кривой радиуса р и правой касательной в(• ) а, расположенной на расстоянии К от (• ) «СК» имеет вид

N= ад²/2р,

так как ad = к l2 - к, го

N= (к l2-К)²12Р. р

Постоянная величина q = 112р назып3ается уr^,ловым коэффициентом. С уче­том углового коэффициента

N = q (К_Р/2 - К)².

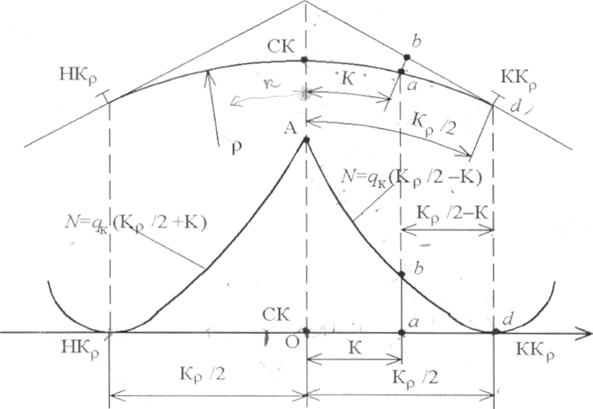
Полученное уравнение нормали является уравнением парабольl, верlцина тсо­торой расrтоJlожена па оси р и сметrzена втlраво па 13еличину К_p/2, т. е. в точке кК_р. Ордината парабольl представляет собой расстояние между кривой радиуса р и правой касательной. Аналогично уравl-iение нормали между кривой радиуса р и правои касательlои

 

66

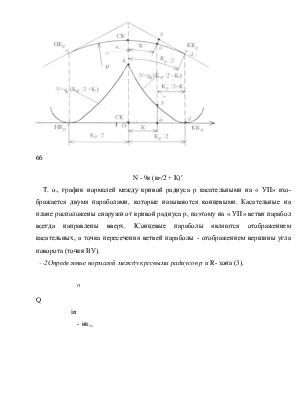
N - 9к (к_Р/2 + К)^г­

Т. о., график нормалей между кривой радиуса р касательными на « УП» изо­бражается двумя параболами, которые называются концевыми. Касательные на плане расположены снаружи от кривой радиуса р, поэтому на « УП» ветви пара­бол всегда направлены вверх. IСонцевые параболы являются отображением касательных, а точка пересечения ветвей параболы - отображением вершины угла поворота (точки ВУ).

--2Оnределение нормалей между кргсвыми радиусов р и R- зона (3).

_О

Q

in

- нк,,

 

 

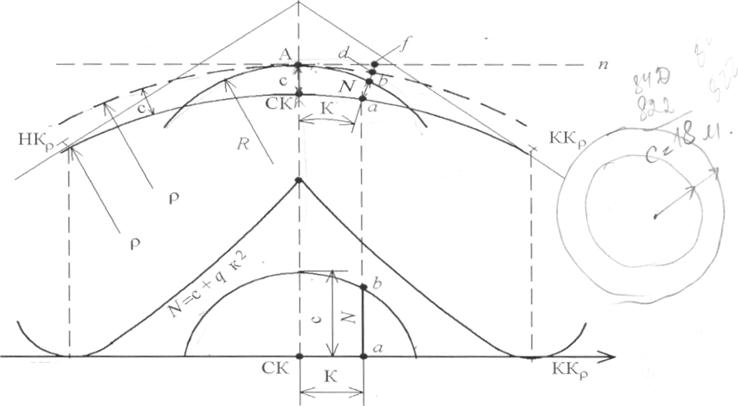
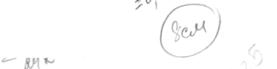
На рисунке переходньlе кривьlе не показаньl, чтобьl не загромождать рису­нок.

Расстояние по биссектрисе межцу кривыми радиусон р и R обозначим через «е». Для вывода уравнения нормали между этими кривыми выпотtним вспомога­тельные построения. Через (•) А проведем кривую радиуса р+ с концентрично кривой радиуса р и через (•) А проведем касательную т- п.

Нормаль в точке а, расположенной на расстоянии К от середины кривой СК (с практически приелллемой точi-тостыо)

N=c-bd.

Как следует из рисунка bd = 6f - df. Полагая величины 6f и df равными

эвольвентам кривых Ab и Ad имеем в

67

Тогда нормаль

6f = К²/2R и clf = К²/2р.

N= с-(К²/2R - К²/2р) = с- К^г/2(1/R - 1/р),
или

N= с+ U2 (1/р - 1/R) К²;

 

введем обозначение

q_n =112 (¹/p_i/R)

и получим

N=c+ n q _К2_.

Уравнение нормали N между кривьlми радиусов р и R является уравнением парабольl. На « УП» эта парабола расположена симметрично относительно оси ординат. Ее вершина находится на расстоянии е от начала координат и назьlва­

ется она проектной. При р> R величина q_n < 0, поэтому ветви парабольl на­

правленьl вниз, что соответствует взаимному расположению кривьlх радиусов р

и R на плане. При р< R ветви проектной парабольl направленьl вверх. На « УП»

проектная парабоJlа является..,.Q:г~а.бражние-м проектнойгкривой радиуса R.

3 определение нормалей между кривой радиуса р и переходньlми кривьlми -

Определению о нормалей в этой зоне предшествует определение элементов переходной кривой - длиньl l и сдвижки - р. Т. к. будем рассматривать симмет­ричную проектную кривую с равньlми длинами переходньlх кривьlх, то все

.,

рассуждения приведем к одной из них, например, левои.

Сдвижка р от переходной кривой на пlrане равна расстоянию между кривой радиуса R и касательной в точке начала кривой радиуса R (НКЮ, отстоящей от «Cк» на расстоsпнии к_Rl2.

На «УП» отображением кривой радиуса R является проектная парабола, а отображением 1<асательной - конlzевая тlарабола. Учитывая эти соответствия, можно на « УП» определить сдвижку р сJlедующим образом. Длина кривой K_R

K_R = Rа_рдд.

зона (2).

____-----­

68

/

 

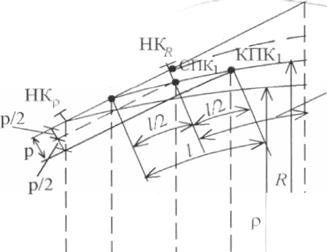
НПК

K_R /2

НК_р

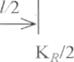
По оси р влево от начала координат откладьlвается величина K_R!2. Через эту точку проводится вертикаль. Отрезок этой вертикали, заключенной между концевой и проектной параболами и есть сдвижка р от переходной кривой. Из изложенного следует, что величина р может бьlть определена графически. При известньlх R и р длина переходной кривой l

I(I/ ∎Rр.

Далее находятся главньlе точки переходной кривой - начала (НПК ₁), середи­на (СПК ₁) и конец (KГIК₁).

На плане НПК ₁ лежит на касательной на расстоянии С/2 влево от начала кри­вой радиуса R (точки H K_R). Чтобьl получить эту точку на «УГI» , откладьlвается на оси р влево от точки с абсциссой K_R12 величина l/2 и проводится через эту точку вертикаль. Точка пересечения этой вертикали с концевой параболой определит точку НПК₁ на « УП».

Конец переходной кривой (КПК₁) на « УП» определяется аналогично. На плане точка КПК₁ лежит на кривой радиуса R вправо от (•) HK_R на расстоянии C12. Для того, чтобьl получить зту точку на «УП» , оттсладьlвается по оси р вправо от точки с абсциссой K_Rl2 величина 112 и через полученную точку проводится

.

 

 

 

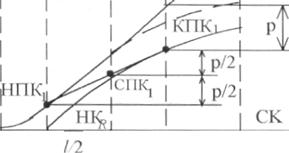
69

вертикаль. Точка пересечения этой вертикали с rlроектной параболой и опреде­лит положение КПК ₁ на « уП» .

Середина переходной кривой как и на плане, на «УП» лежит на середине от­резка р.

Ординатьl переходной кривой относительно касательной b в соответствии с

рисунком определяются

 

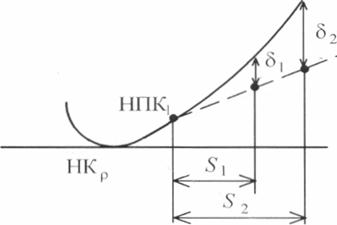
где s - расстояние от начала

.,

переходнои кривои до точки, в которой определяется ё.

На плане величина b откладывается от касательной. На «YII» величиньl b от­кладьlваются от отображения касательной (концевой парабольl) вниз.

График нормалей для правой переходной кривой строится аналогично.

Определение сдвигов и построение графика сдвигов

Определение сдвигов ар суЩествуюЩей кривой относительно кривой радиу­са р может бьlть произведено любьlм способом, наиболее часто - метод угловьlх диаграмм. ВеJтичипа радиуса может бьrть назначена произвольно, желательно, чтобьl К _p > К~, т. к. в противном случае при построении графика сдвигов и переходной кривой имеются некоторьlе неудобства.

При k _р > К_с график сдвигов на всем протяжении К_с строится от оси р. Концьl суЩествуюlцей кривой () А₁ и Г ₁ в этом случае лежат на внутренних ветвях концевьlх парабол.

При К_р < К~ сдвиги ар в интервале НК_р КК _Р строятся от оси также, как и в предьlдуЩем случае. На участках А₂ - НК_р и КК_Р Б₂ сдвиги представляют собой расстояния между касатеJlьньlми и существующей кривой. На « УП» отображе­ниями касательньlх являются концевьrе rlарабольl. Поэтому на участках А₂ - НК_р и КК_Р Г~ расстояния откладьlваrотся по оси р, а сдвиги на «УП» должньl

откладьlватыя вниз от внешгlих вствеи концевьlх парабол. .

70