Термодинамика. Термодинамические процессы, виды энергии и их особенности, теплообмен, страница 2

Учитывая, что эти формы независимы:

“+” - если теплота подводится; “-“ - если отводится.

Прежде всего в качестве работы учитывают работу изменения объма:

Р     F

dx

                                                    

Работа тела против внешней среды: ,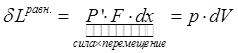

где  - это условие справедл., если проц. равновес. (нет диссип. и проц. протек. очень медленно). Это предельный случай действит. проц. В реал. проц., когда скорость проц. конечна  за счет вязкого трения внутри системы работа будет производится меньше.

Работа по преодол. трения:

В действит. проц. давление внутри тела будет в каждой точке различно. Поэтому вводят среднее давление .

При работе расширения: 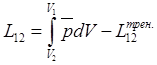. По этому ур-ю можно ввести в рассмотрение - координаты:                      Р    

Работу трения представить в                      1

  - координатах невозможно.

Штриховой линией показан соответств.

равнов.

 проц.                                                                                                          

                                                                                                        2’

                                                                                                                    2

                                                                                                                    V

Если учитывать только работу изменения объема, то 1-й з-н в квазиравновесном приближении для закрытой системы (при ):

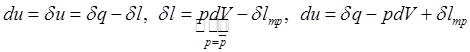
Работа от трения предст. собой частный случай энергии диссип. : .

Энергия диссип. проявл-ся всегда в виде теплоты диссип. Поэтому в квазиравн. приближ.:  - аналитическое выражение 1-го з-на т/д для неподвижного тела или движущегося тела при .

Часто удобно вместо внутр. эн. использовать энтальпию:

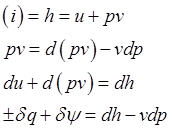,  - это означ., что тепл. может подв. или отвод-ся.

Энергия диссипации всегда положительна.

5. Энтропия как критерий теплообмена и внутренних диссипативных проц-в. Аналитич-е выраж-е 2-го з-на т/д в квазиравн. приближ. Перенос и произв-во энтропии.

Причина необратимости реал-х проц-в явл-ся конечная скорость этого процесса, кот-я всегда связана с наличием разности предельных величин ( и т.д.). Т.к. любая система стремится к равновессию, то очевидно стремление системы выровнять давление, темпер. и др. параметры. Принято вводить естественные (положит-е) процессы и отриц-е (которые сопровожд. затратой дополн-й энергии). Критерием, который хар-ет необратимость процесса явл-ся энтропия.

2-й з-н т/д: Любые реал-е процессы в природе протекают неравновесно, необратимо, т.е. всегда сопровожд-ся диссипацией энергии.

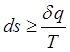- 2-й з-н.

При этом всегда энтропия увеличивается.

                                                        теплоизолир. оболочка

А

В

                                                       

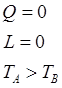
Для данной сист. 1-й з-н: , , , .

Теплота, кот-я от гарячего тела передается холодному:  .

Теплота, кот-я воспринимается: .

Энтропия: .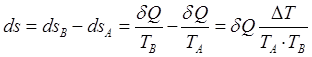

Общее изменение энтропии равно сумме изменений энтропий тел. Энтропия системы будет возрастать. Из последней формулы видно, что повышение энтропии будет тем больше, чем меньше температурный уровень тела.

1-й з-н не может показать направление процесса (это просто баланс энергий). Поэтому он должен быть дополнен 2-ы з-ном, кот-й хар-ет направление процесса:

, поделим лев. и прав. части на Т: 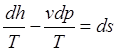, 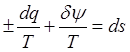- энтропия может меняться за счет теплообмена и диссип-и внутри системы.

Если проинтегрировать 2-й з-н: 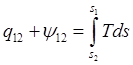. Если теплообменом можно пренебречь . Энтропия не меняется – изоэнтропный процесс. Из последнего ур-я следует, что теплота  равна по модулю энергии диссипации. Для предельного процесса идеального .

2-й з-н позволяет рассчитать изменение энтропии системы, как функции состояния.

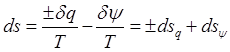, - энтропия системы может изменятся за счет подвода теплоты через границу (теплообмена).

6. Идеально-газовое состояние вещества. Определение термических и калорических параметров. Удельная теплоемкость и показатель изоэнтропы.

Идеально-газовое состояние вещества – состояние вещества, при котором можно пренебречь (не учитывать) взаимодействием молекул, что приводит к упрощениям.

Если мы для идеального газа находим изменение функции, которое не зависит от пути процесса, поэтому можно использовать модель равновесного процесса.

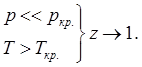 Калорические параметры идеального газа не зависят от р. Для идеального газа прежде всего зависимость от температуры. Теплоемкость иногда зависит от температуры.

	Исключение составляют одноатомные газы. Для двух и трех атомных молекул:  показатель изоэнтропы (меняется с ростом температуры).

 

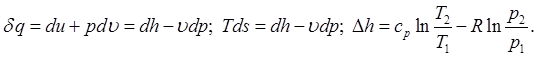
Для смеси ид газов справедлив принцип аддетивности (необходимо знать состав газа)

Закон Дальтона: сумма парц давл всех компонентов смеси составляет давл всей смеси.

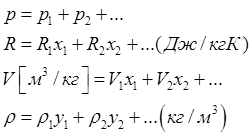  у-объемная концентрация, х- массовая.

- зависимость между масс и объемными концентрациями.

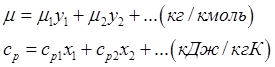
Отличие от принципа аддетивности представляет определение энтропии смеси газов. Энтропия смеси всегда выше, чем энтропия компонентов в отдельности до смешивания. При смешивании каждый компонент оказывается при более низком давлении равном парциальному давл в смеси, т.е. происходит дросселирование каждого компонента от первоначального давления до парциального. Энергия не меняется, а происходит резкое падение эксэргии.  

При дросселировании (адиабатном) (течение через сопротивление) большие потери на трение (большое )