Математическое моделирование горизонтальных придонных ярусов, выметаемых под углом к течению

УДК 639.2.081.001.57.681.3

, Л. А.  

Дальрыбвтуз, Владивосток

Математическое моделирование горизонтальных придонных ярусов,

выметаемых под углом к течению

На  Дальнем Востоке используются донные ярусы, которыми  ловят таких гидробионтов, как треска  и палтус. Причём выметка ярусов осуществляется параллельно течению. При выметке ярусов параллельно течению запаховые поля отдельных наживок перекрываются, и общий объём запаховых полей всех наживок минимальный, а значит, минимальна и уловистость яруса. В Японии [14] и на Северном бассейне России [11] для получения максимальной уловистости ярусов их выметку осуществляют перпендикулярно течению. При этом общий объём запаховых полей всех наживок будет максимальным.

Поэтому актуальна задача формирования математических моделей, алгоритмов и программных комплексов, позволяющих моделировать горизонтальные ярусы, выметаемые  под углом к течению.

Попытки решить эту проблему для придонных ярусов методом проб и ошибок, предпринятые в своё время РК «Восток-1», не увенчались успехом. Что показало невозможность решать многие практические задачи промышленного рыболовства, без использования методов математического моделирования.

Крючковые снасти являются классическими орудиями рыболовства. Их совершенствованием занимаются многие исследователи: ВНИРО [8 - 10], ПИНРО [11], КамчатНИРО [1].

Большой импульс исследованию ярусов дала монография Н.В. Кокорина [8]. По существу с выходом этой монографии начались глубокие исследования механики ярусов на Дальнем Востоке, выполняемые в  Дальрыбвтузе [3-7]. Оптимизация параметров любых орудий рыболовства, в том числе и крючковых, возможна только с помощью математического моделирования. Математическое моделирование предполагает разработку триады:

 математическая модель (ММ) - алгоритм (А) - прикладной программный комплекс (ППК).

Основными элементами любых ярусных систем являются канаты, поэтому в основе исследования ярусов лежит математическая модель (ММ)  каната. Используются три математические модели каната:

1.  ММ на основе цепной линии при отсутствии течений;

2.  плоская ММ при наличии течений;

3.  пространственная ММ при наличии течений.

До последнего времени многие исследователи рыболовных систем использовали ММ цепной линии, разработанной выдающимися классиками Г. Лейбницем, Х. Гюйгенсом, И. Бернулли [12]

В данной работе содержится общая постановка и решение задачи моделирования  придонных горизонтальных ярусов с одним буём посередине каждого участка, устанавливаемых как параллельно течению, так и под любым углом к течению, в том числе и перпендикулярно. Приводятся также результаты экспериментального исследования отрезков ярусов, выполненные в аэродинамической лаборатории НБАМР.

На рис. 1 показан  горизонтальный придонный ярус с буем посередине каждого участка, выметаемый под углом  к течению.

Если ось земной системы координат совместить с осью  поточной системы координат , то форма хребтины яруса будет описываться системой дифференциальных уравнений:

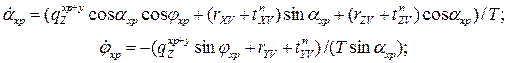
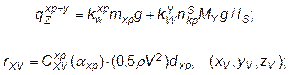                                        (1)

,

;

;

 (xp, n), где  – проекция на ось  веса в воде 1 м хребтины с узлами крепления к ней крючковых поводцов;  – масса узла крепления поводца к хребтине;  – диаметры хребтины и поводца;  – длина поводца;

 – проекции на оси x, y, z земной системы координат натяжений крючковых поводцов, приходящихся на единицу длины хребтины; ,(x, y, z) – проекции гидродинамических сил поводца и наживки с крючком; – угол атаки поводца;  - натяжение, угол атаки хребтины и угол крена плоскости потока хребтины в текущей точке; - проекции гидродинамических сил, приходящихся на 1 м хребтины, на оси поточной системы координат; – веса в воде поводца и наживки с крючком соответственно;  - линейные плотности поводца и хребтины.

Так как каждый участок яруса состоит из двух секций, то при расчёте характеристик яруса на участке   приходится дважды решать задачу Коши для системы (1).

Вначале рассчитывается первая секция хребтины яруса . Начальные данные для этой секции – это параметры хребтины в точке :

·   угол атаки хребтины в точке  -

·   угол крена плоскости потока хребтины в точке  - ;

·   натяжение хребтины в точке  - .

Здесь , - натяжение хребтины при заданной скорости течения V и натяжение  при скорости течения, равной нулю (); - проекции на оси x и z натяжения хребтины в точке  при скорости течения равной нулю. Для яруса с промежуточным буём посередине они определяются по формулам: