Розробка комплексу рекомендацій по удосконаленню аналізу зменшення витрат на підприємстві агрофірмі «Зоря» ТОВ

3. РОЗРОБКА КОМПЛЕКСУ РЕКОМЕНДАЦІЙ ПО УДОСКОНАЛЕННЮ АНАЛІЗУ ЗМЕНШЕННЯ ВИТРАТ НА ПІДПРИЄМСТВІ АГРОФІРМІ «ЗОРЯ» ТОВ.

3.1. Побудова економетричної моделі

За допомогою економетричної моделі розглянемо вплив на матеріаломісткість (У) таких факторів як: зменшення витрат на корми та добрива (Х2) та врожайність сільськогосподарських культур і продуктивність худоби (Х1). Оскільки матеріаломісткість є одним з ключових показників ефективності використання матеріальних витрат, доля яких у сукупних витратах підприємства є найзначущую. Тому розгляд моделі буде надзвичайно актуальним для підприємства. Використаємо метод множинної кореляції.

Дані для аналізу представлено у таблиці 3.1.

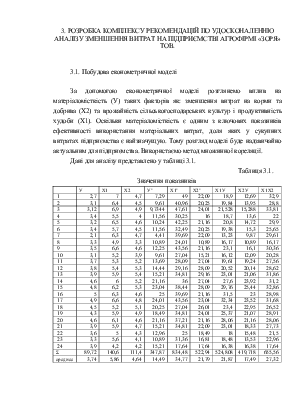
                                                                                                  Таблиця 3.1.

Значення показників

Отже, за отриманими даними побудуємо економетричну модель та всебічно оцінимо вплив факторів на матеріаломісткість.

 У = b0+b1X1+b2X2

 D (X) = Х²-Х², σ(X) = √ D (X)

 D (X1) = 0,45,  σ(X1) = 0,63

 D (X2) =0,24,  σ(X2) = 0,49

 D (Y) = 0,52,  σ(Y) = 0,72

Рівняння в стандартизованих змінних:

ty = β1tx1+β2tx2, где ty – нормована випадкова величина

Складемо систему нормальних рівнянь відносно β-коефіціенту

β1+β2 rх1х2= rух1

β1 rх1х2 + β2 = rух2

Розрахуємо коефіцієнт регресії, за допомогою якого розрахуємо щільність зв’язку.

 r = (ХіУ-Хі*У)/ σхі σу

rух1 = 0,07

rух2 = 0,39

rх1х2 =0,42

Спостерігається мультіколініарність, оскільки зв’язок між показниками х1х2 найщильнший.

β1+0,42β2 = 0,07

0,42β1 + β2 = 0,39

Щоб розрахувати коефіцієнти розрахуємо наступні показники:

∆ = 0,82, ∆1=-0,09, ∆2=0,036

β1=∆1/∆, β1 = -0,11,

β2=∆2/∆, β2 = 0,04.

          Таким чином, ty = 0,04tx2-0,11tx1.

          Це говорить про те, що збільшуючи врожайність с/г культур і продуктивність худоби на 0,63 млн. грн. (при витратах на корми та добрива на середньому рівні) матеріаломісткість збільшилася на 4%. Порівняно з величиною 0,72 млн. грн. При зменшенні витрат на корми та добрива на 0,49 млн грн.. (при врожайності с/г культур і продуктивності худоби на середньому рівні) матеріаломісткість зменшиться на 11%, порівняно з величиною 0,72 млн грн. Таким чином, матеріаломісткість у більшому ступені від зменшення на корми та добрива.

Отримаємо рівняння в натуральних змінних.

У = b0+b1X1+b2X2

bі = βі σу/ σхі,

b0 = у - b1X1 - b2X2.

b1 = -0,13

b2 = 0,06.

b0 = 4,22.

У = 4,22 – 0,13X1  + 0,06X2.

Розрахуємо коефціент детермінації:

R = √ ryх1β1+ ryх2β2

R = 0,11,

R² = 0,3317.

Таким чином,  33,17% змінності матеріаломісткості залежить від факторів, включених до моделі та на 66,83% від факторів, не включених до моделі.

Перевіримо значущість множественного коефіцієнту кореляції по критерію Фішера, тобто адекватність моделі.

F=(R/m)/(1-R²)/(n-m-1),

де m – кількість факторів;

     n – кількість спостережень.

F емп. = 3,75.

F емп > F0,05, тобто, Но відкидається на користь альтернативної Н1: R≠0.

А Отже, модель адекватна.

          Розрахуємо еластичність, а саме часні коефіцієнти еластичності матеріаломісткості.

          Е у/хі = bі*Хі/У,

          Е у/х1 = 0,2.