Лекция № 11. Продолжение. (уч. Одинокова. Стр.75, … , 111).
Приравнивая (2.26) и (2.27), можем записать:
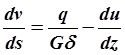 .
.
Подставим в
это выражение 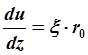 из (2.24) и умножим на
ds:
из (2.24) и умножим на
ds:
получим ![]()
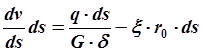 (2.28)
(2.28)
На рис 2.40
легко видно, что ![]() , где dωo – площадь элементарного сектора с вершиной в точке О
и основанием ds (на рисунке
заштрихована). Условимся относительно знака площади ω. Будем
считать площадь ω положительной, если она образуется вращением
радиуса вектора относительно точки О по часовой стрелке, и
отрицательной при обратном вращении. Проинтегрируем теперь выражение (2.28) в
интервале между двумя смежными продольными рёбрами
, где dωo – площадь элементарного сектора с вершиной в точке О
и основанием ds (на рисунке
заштрихована). Условимся относительно знака площади ω. Будем
считать площадь ω положительной, если она образуется вращением
радиуса вектора относительно точки О по часовой стрелке, и
отрицательной при обратном вращении. Проинтегрируем теперь выражение (2.28) в
интервале между двумя смежными продольными рёбрами 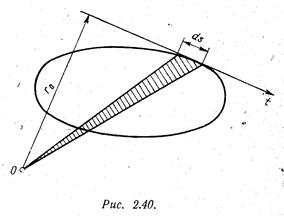
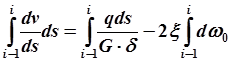 . (2.29)
. (2.29)
Первый интеграл даст, очевидно, разность осевых смещений двух смежных рёбер (vi – vi -1), последний интеграл даст ( ω0i – ω0 i – 1), т.е. площадь сектора, соответствующую дуге обшивки между двумя смежными рёбрами. Рассмотрим третий интеграл:
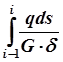 .
.
В интервале между двумя смежными рёбрами G и δ можно считать постоянными (Gi , δi), погонная касательная сила q также не может изменяться по s, так как в этом интервале в соответствии с нашим предположением отсутствуют нормальные напряжения. Действительно, условие равновесия обшивки между стрингерами запишется в виде
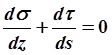 , так как в обшивке между стрингерами σ
= 0,
, так как в обшивке между стрингерами σ
= 0,
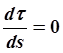 , следовательно,
, следовательно, 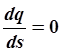 и интеграл запишется так:
и интеграл запишется так: 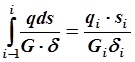 , гдеsi – длина
дуги контура между рёбрами i – 1 и i.
, гдеsi – длина
дуги контура между рёбрами i – 1 и i.
Таким образом, уравнение (2.29) принимает следующий вид
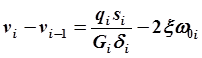 ,
(2.30)
,
(2.30)
где ω0i = ω0i – ω0, i -1 – площадь сектора, ограниченного радиусами-вектрами, проведенными из мгновенного центра в точки i и i – 1, и дугой контура si.
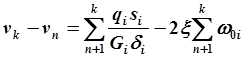 Мы получили выражение для относительного
осевого смещения двух смежных рёбер. Из этой формулы легко получить
относительное перемещение любых рёбер сечения. Для этого достаточно
просуммировать выражение (2.30). Так, например, если мы хотим найти осевое
смещение k-го ребра относительно п-ного, достаточно
просуммировать (2.30) от п+1 до k. Получим
Мы получили выражение для относительного
осевого смещения двух смежных рёбер. Из этой формулы легко получить
относительное перемещение любых рёбер сечения. Для этого достаточно
просуммировать выражение (2.30). Так, например, если мы хотим найти осевое
смещение k-го ребра относительно п-ного, достаточно
просуммировать (2.30) от п+1 до k. Получим
(2.31)
Формулы (2.30) и (2.31) устанавливают связь осевых перемещений рёбер с касательными усилиями в сечении тонкостенной балки и её деформациями.
Если известны погонные касательные усилия, а также прогибы конструкции и относительный угол закручивания, то мы могли бы вычислить осевые смещения всех рёбер и, следовательно, определить депланацию сечений. Действительно, по прогибам и углу закручивания мы определили бы мгновенный центр О, а тем самым и все wо i ,и далее по формуле (2.31) нашли бы депланации.
Особенно легко разрешается эта задача при кручении тонкостенной балки с сечением, имеющим две оси симметрии. Тогда, очевидно, точка О совпадает с точкой пересечения осей симметрии и wо i определяются сразу.
Не будем останавливаться более подробно на исследовании полученной формулы, так как это преждевременно. К этой формуле возвратимся позднее, когда возникнет необходимость изучать депланации сечений конструкции. Здесь воспользуемся этой формулой для получения более простой зависимости, являющейся её следствием.
Пусть сечение конструкции имеет замкнутый контур с п рёбрами (рис. 2.41).
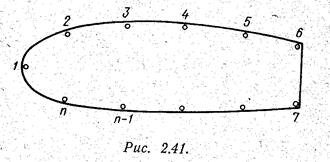 Формула (2.31)
даёт нам осевое смещение любого k-го ребра. Воспользуемся тем, что
контур замкнут, и найдём осевое смещение ребра п по отношению к самому
себе. Это смещение, очевидно, будет равно нулю. Запишем это смещение, пользуясь
формулой (2.31) и приняв во внимание, что в силу замкнутости ребро (п+1)
будет первым
Формула (2.31)
даёт нам осевое смещение любого k-го ребра. Воспользуемся тем, что
контур замкнут, и найдём осевое смещение ребра п по отношению к самому
себе. Это смещение, очевидно, будет равно нулю. Запишем это смещение, пользуясь
формулой (2.31) и приняв во внимание, что в силу замкнутости ребро (п+1)
будет первым
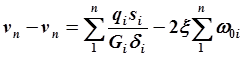 |
.
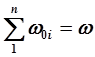 |
Но нетрудно видеть, что , где ω – это площадь. Ограниченная контуром сечения.
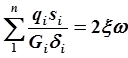 |
Следовательно, (2.32)
Получена, таким образом, зависимость между погонными касательными силами и относительным углом закручивания. Эта зависимость является следствием замкнутости контура и называется поэтому условием замкнутости контура.
Эта формула впервые была получена В.Н. Беляевым для случая чистого кручения энергетическим методом. В действительности, как мы видим, она имеет место в самом общем случае напряжённого состояния конструкции постоянного сечения, если применима гипотеза о неизменности формы контура поперечного сечения. Л.И. Балабух показал, что эта формула с несколько иным толкованием δ применима и к конусным балкам.
Условие замкнутости контура мы широко будем использовать в дальнейшем, избегая, таким образом, необходимости обращаться к энергетическим методам.
Формула (2.31) получена для произвольного контура. Если контур сечения многосвязный, можно, очевидно, получить не одну, а несколько зависимостей типа (2.32), применив тот же приём к каждому замкнутому контуру сечения. Например, для контура, изображённого на рис 2.42, получим три условия замкнутости:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.