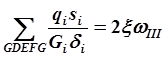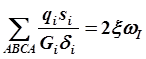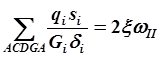Расчет на сдвиг и кручение. Отделение сдвига от кручения, страница 2

 

1)                                   ;    2)                                   ;  3)                                         .

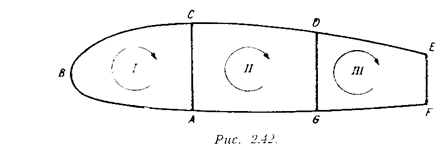
Нетрудно видеть, что выбор замкнутых контуров в сечении можно осуществить в разных вариантах и каждый раз соответственно преобразуются суммы. Так, для того же сечения мы сможем записать условие замкнутости контуров: ABCDEFGA,  ACDEFGA, GDEFG. Соответствующие условия замкнутости запишутся:

                             

                                                                     

         

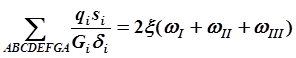
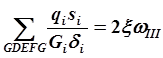
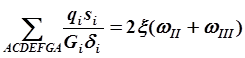
Они, очевидно, представляют собой лишь линейную комбинацию прежних уравнений.

2.  РАСЧЁТ НА СДВИГ

2.5.1. Отделение сдвига от кручения.

В предыдущих разделах курса ознакомились с расчётом крыла на изгиб. В действительном крыле изгибающие моменты вызываются поперечной нагрузкой, расчёт на изгиб должен быть дополнен расчётами на сдвиг и кручение.

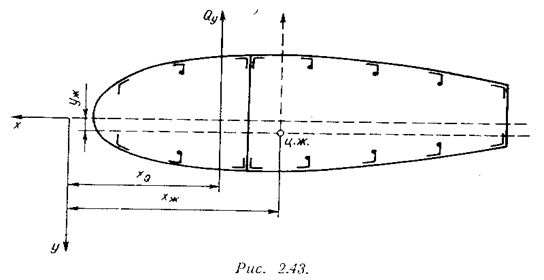Допустим, что в сечении крыла, изображённом на рис. 2.43, действует поперечная сила Q_y ,нормальная к нейтральной оси х. В общем случае, сила  Q_y будет вызывать сдвиг в сечении и закручивание. Степень закручивания данного сечения  (величина угла ξ) будет, очевидно, зависеть от положения силы  Q_y . Ясно, что если мы будем сдвигать силу в сторону носка крыла, сечение будет закручиваться по ходу часовой стрелки и относительный угол закручивания будет возрастать. Наоборот, при смещении силы  Q_y  в другом направлении угол закручивания будет убывать и в какой-то момент сменит знак – сечение будет закручиваться в другую сторону. Отсюда следует, что всегда можно найти такое положение силы Q_y , при котором относительный угол закручивания сечения равен нулю. Отметим соответствующую абсциссу х_ж .

Если введём теперь в рассмотрение вместо силы  Q_y силу  Q_х , направленную по оси х, то аналогично сможем прийти к выводу, что сила  Q_х при каком-то положении по вертикали также не даст закручивания данного сечения. Пусть соответствующая этому положению ордината будет у_ж  (см. рис. 2.43). Пересечение этих двух направлений даст нам точку, которую по аналогии с соответствующей точкой в лонжеронном крыле мы назовём центром жесткости. Пока не известно, как найти такую точку в сечении тонкостенного крыла, не знаем также, зависит положение этой точки от величины нагрузки или нет. В данный момент достаточно очевидно существование такой точки для заданных сил.

Итак, если нам задана сила  Q_y ,мы всегда сможем перемещая её по хорде, найти такое её положение, когда относительный угол закручивания данного сечения будет равен нулю.

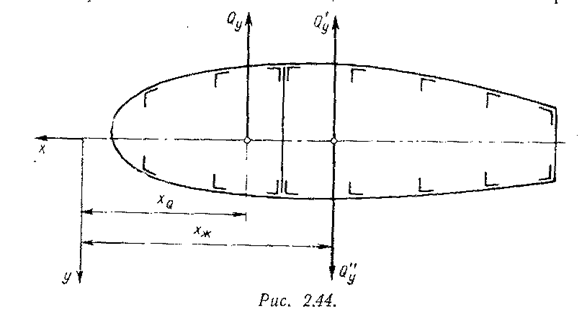
На рис 2.44 отметим эту абсциссу х_ж.  Она пока неизвестна. Приложим к сечению по линии х = х_ж две силы:  Q_y' и  Q_y", параллельные силе  Q_y , причём  Q_y'= -  Q_y"=  Q_y .

Введение этих сил в систему действующих не изменит, очевидно, напряжений и деформаций крыла, так как они взаимно уравновешены в одной точке.

Теперь нетрудно усмотреть, что сила  Q_y' с абсциссой, равной х_ж , даст только сдвиг сечения без закручивания, так как она проходит через центр жёсткости, а силы  Q_y и  Q_y"дадут закручивающую пару М_кр =  Q_y(х_Q – x_ж).

Таким образом, понятие центра жёсткости даёт нам возможность разделит нагружение на:

1. сдвиг силой  Q_y' =  Q_y(ξ = 0);
2. кручение моментом М_кр =  Q_y(х_Q – x_ж). 

При этом для расчёта на сдвиг не требуется знания положения центра жёсткости, так как только крутящие моменты зависят от его координаты. Следовательно, если мы знаем поперечную силу в сечении, мы сразу можем производить расчёт на сдвиг, предполагая, что сила  Q_y нами перенесена, как это мы сделали сейчас, в центр жёсткости сечения.

От поперечной нагрузки на конструкцию крыла в сечении одновременно будет действовать изгибающий момент, вызывающий нормальные напряжения,  и поперечная сила, вызывающая касательные напряжения. Очевидно, что те и другие напряжения в отдельных элементах конструкции должны быть в равновесии. Используем эти условия равновесия для определения касательных напряжений по найденным ранее нормальным напряжениям при изгибе.

При решении будем использовать принятые ранее предположения.

1. Касательные напряжения по толщине обшивки и стенок лонжеронов не меняют своей величины и направлены по касательной к контуру. Это позволяет ввести в рассмотрение вместо касательных напряжений погонные касательные усилия q = τδ.
2. Обшивка и стенки лонжеронов не воспринимают нормальных напряжений. Площади присоединённых полос обшивки отнесём к площади рёбер (стрингеров и полок лонжеронов).
3. Сечение конструкции пока будем считать переменным по длине, но угол наклона образующей к оси z малым, так что косинус угла наклона можно считать равным единице.