Лекция № 12. Расчёт напряжений и деформаций при стеснённом кручении.
Стесненное кручение тонкостенных конструкций открытого сечения.
Расчет напряжений и деформаций.
Стесненным называется кручение, где наряду с касательными напряжениями возникают и нормальные напряжения. Не следует путать с явлениями в замкнутых контурах, где нормальные напряжения являются следствием несовместности деформаций. В данной задаче и касательные, и нормальные напряжения статически необходимы.
Допустим, что тонкостенная балка произвольна, но постоянного по длине сечения нагружается крутящим моментом. Требуется найти напряжения и деформации конструкции.
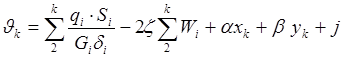
Воспользуемся
гипотезой Власова о ничтожности деформации сдвига в панели, то есть 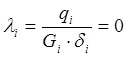 , тогда депланация запишется в виде:
, тогда депланация запишется в виде:
![]()
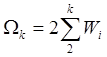 - секторальная координата ребра «к»
отсчитанная от края сечения, (от точки 1 – в нашем случае).
- секторальная координата ребра «к»
отсчитанная от края сечения, (от точки 1 – в нашем случае).
Если известны перемещения по оси z (вдоль контура), то можно найти и деформации ребер, и силы, действующие в них.
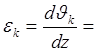
![]()
где: ![]() -
перемещение;
-
перемещение;
z – длина.
![]()
![]()
![]()
![]() (
(![]() )
)
Поскольку внешней нагрузкой сечения является только крутящий момент, внутренние усилия конструкции должны удовлетворять следующим уравнениям равновесия (**):
1. 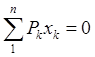 4.
4.
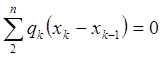
![]()
![]()
2. 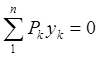 5.
5. 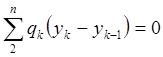
![]()
![]()
3. 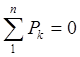 6.
6.
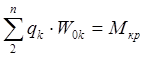
![]() - площадь секторов с вершинами в
центре жесткости.
- площадь секторов с вершинами в
центре жесткости.
Подставляем ![]() из (
из (![]() )
)
![]()
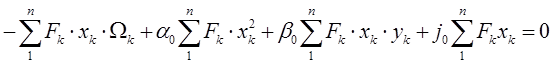
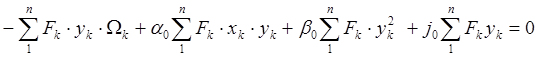
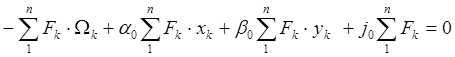
![]()
Если за оси взять главные центральные оси сечения, то
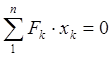
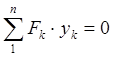
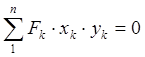
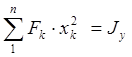
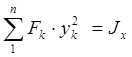
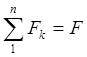
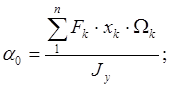
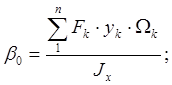
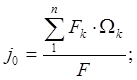
![]()
Тогда:
![]() ;
;
![]()
![]() -
называется главной секториальной координатой ребра «к».
-
называется главной секториальной координатой ребра «к».
Из последней формулы видно, что при кручении тонкостенной балки открытого контурного сечения нормальные напряжения пропорциональны главным секториальным координатам. Главным секториальным координатам удовлетворяют соотношения:
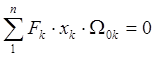
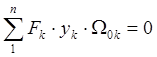
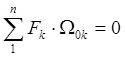
Центром главных секториальных площадей будет центр жесткости сечения.
Центр кручения совпадает с центром жесткости.
Рассмотрим погонные касательные усилия:
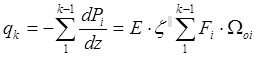 (
(![]() )
)
Подставляем ![]() в 4 и 5 уравнения (
в 4 и 5 уравнения (![]() ):
):
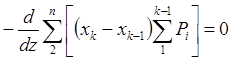
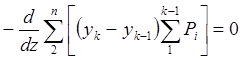
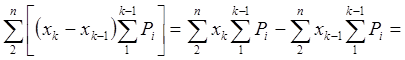
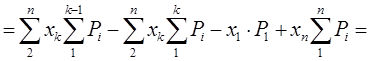
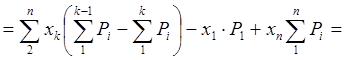
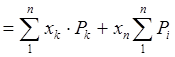
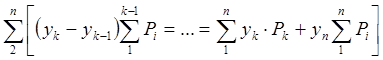
Полученные суммы в силу первых
трех уравнений (![]() ) обращаются в ноль.
Следовательно, эти уравнения тождества.
) обращаются в ноль.
Следовательно, эти уравнения тождества.
Преобразуем последнее уравнение
системы (![]() ):
):
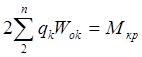
![]()
Подставляем в уравнение (![]() ), получим:
), получим:
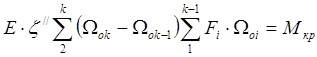
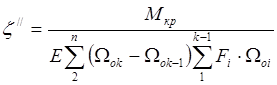
Преобразуем сумму в знаменателе:
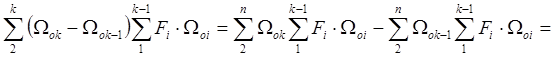
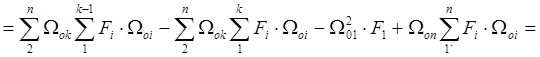
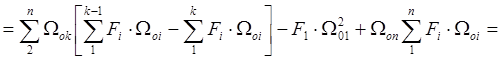
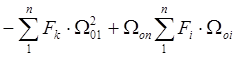
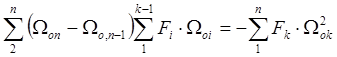
Тогда формула (![]() ) принимает вид:
) принимает вид:
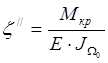
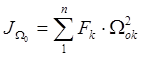
![]() - главный сектор момента инерции
сечения.
- главный сектор момента инерции
сечения.
Проинтегрируем последнее уравнение:
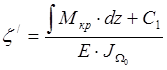
![]() где:
где:![]() - бимомент.
- бимомент.
Так как 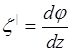 ,
получим:
,
получим: 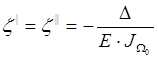
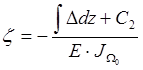 , тогда
, тогда 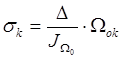
![]() и
и ![]() определяются
из краевых условий для каждой конкретной задачи; депланация сечения примет вид
определяются
из краевых условий для каждой конкретной задачи; депланация сечения примет вид
![]() . Она пропорциональна главной секториальной
координате:
. Она пропорциональна главной секториальной
координате:
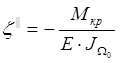 (1)
(1)
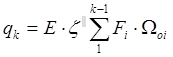 (2)
(2)
Подставляем (1) в (2), имеем 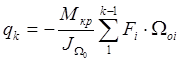
Обозначаем 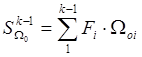 , тогда
, тогда 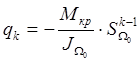 .
.
Где: ![]() -
секториальный статический момент площадей.
-
секториальный статический момент площадей.
Эта формула напоминает формулу определения потоков касательных сил при поперечном сдвиге.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.