Депланация сечений при сдвиге-кручении. Учёт конусности крыла

ПРОЧНОСТЬ  КОНСТРУКЦИЙ

6 – й семестр, 3 – й курс.  2011 г.

Раздел 5. Расчёт элементов крыльев

5.1. Депланация сечений при сдвиге-кручении

Лекция № 11.

(материал излагается на основе уч. Зайцева В.Н. гл. 3. § 8. стр. 112…).

§ 8 Учёт конусности крыла

Конусность крыла создаётся за счёт его сужения и за счёт изменения толщин профилей и обшивки по размаху. Влияние конусности на нагружение элементов каркаса рассмотрим на примере лонжерона (см. рис. 3.25).

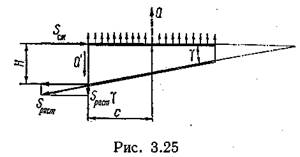От внешней нагрузки в поясах лонжерона возникают осевые усилия, в стенках – сдвигающие. Конусность практически не влияет на значение осевых сил в поясах лонжерона и, в то же время, существенно сказывается на значении касательных усилий в стенках. Из-за наклона поясов часть поперечной силы лонжерона уравновешивается вертикальными составляющими осевых сил, возникающих в поясах. При этом поперечная сила стенки соответственно изменяется.

Из условия равновесия сил в проекции на ось у, полагая sin γ ≈ γ, получим выражение для поперечной силы стенки:

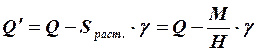,                               (3.26)

где  М = Q·с – изгибающий момент лонжерона в рассматриваемом сечении. Величина 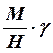- может достигать 20 – 35% от силы Q. Поэтому, определяя касательные усилия в стенках, учитывать конусность необходимо.

Влияние сходимости продольных элементов в плане крыла на величины сдвигающих усилий в обшивке учитывают аналогично.

§ 9. Деформации крыла

От действия внешних нагрузок крыло изгибается и закручивается. Деформации крыла характеризуются прогибами у его сечений и углами закручивания φ.

Крыло рассматривается как балка, защемлённая у борта фюзеляжа, за её упругую ось z принимается ось жёсткости крыла.

9.1. Деформации изгиба крыла – прогибы у и углы поворота поперечных сечений

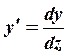 (девиацию) – определяют, интегрируя дифференциальное уравнение упругой оси крыла 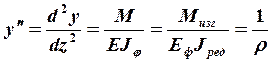          ,                                          (3.27), где М = М_изг. – изгибающий момент в сечении; ЕJ_φ – жёсткость при изгибе; Е_ф – модуль упругости для фиктивной прямолинейной диаграммы ; J_ред – редуцированный момент инерции всего сечения; ρ – радиус кривизны упругой оси.

Если схематизировать крыло как двухпоясную балку с высотой Н и равными редуцированными площадями поясов (панелей) F, то

.

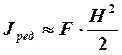Девиация (угол наклона касательной к изогнутой оси, или как угол поворота поперечных сечений), определяется как интеграл функции .

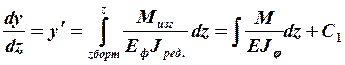 - угол поворота сечения;

и прогибов, как интеграл функции у΄:

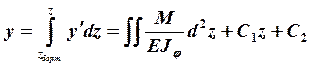                                                    (3.28)

Постоянные интегрирования С₁ и С₂ определяются из граничных условий: при z = 0 (см. рис. 3.26) угол поворота у΄= 0,  при z = l_ф прогиб у = 0. Приближённо крыло можно рассматривать как балку, защемлённую у борта фюзеляжа. В этом случае у борта фюзеляжа z = l_ф, у = у΄ = 0 и  С₁ = С₂ = 0.

Обычно М и EJ_φ  в виде аналитической функции задать не удаётся. Поэтому практически интегрирование уравнения упругой оси осуществляют графоаналитическим способом. За упругую ось z принимают ось жёсткости крыла. Вначале строят эпюру 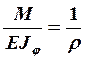 делением ординат эпюры М на соответствующие ординаты эпюры EJ_φ. Последовательное суммирование площадей полученной эпюры от оси самолёта к концу крыла даёт эпюру девиаций у΄, а суммирование эпюры у΄ при выполнении граничных условий в точке z = l_ф – эпюру прогибов у.

Прогибы крыла, кроме того, можно найти, выразив функцию  через напряжения.

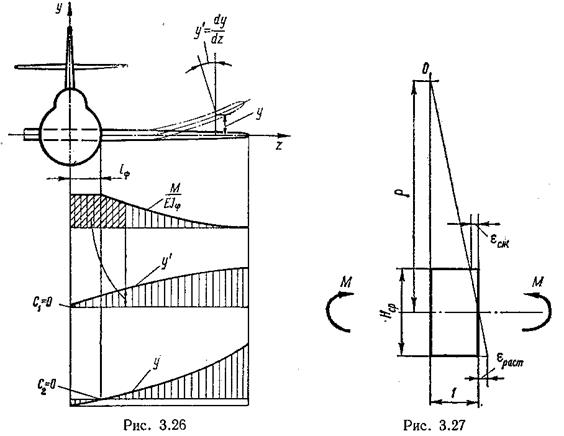
Рассматривая деформированный отсек крыла единичной длины (рис. 3.27) и учитывая, что , найдём:

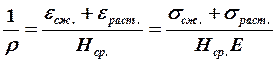, где σ_сж., σ_раст. – напряжения в сжатой и растянутой панелях крыла при действии на крыло эксплуатационного момента.

Для приближённой оценки прогибов можно считать, что крыло имеет призматическую форму и выполнено равнопрочным, т.е. Н = const,  σ_сж. =  const  и σ_раст. =  const.  Тогда, выполняя интегрирование уравнения для консоли крыла, получим формулу для определения прогиба на конце крыла в виде

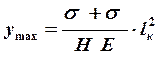,                                    (3.29)

где Н_ср. – средняя высота кессона в корневом сечении крыла;

l_к – длина консоли.

Пример.  Пусть σ_сж. = σ_раст. = 25 кГ/мм², длина консоли l_к = 5 м, высота кессона Н = 25 см, материал – дуралюмин, Е_Д16 = 7· 10⁵ кГ/см². Тогда прогиб конца крыла составляет:

.

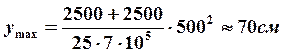Прогибы крыла тем больше, чем больше изгибающий момент и чем крыло тоньше., так как , где Н – толщина крыла. У современных самолётов при эксплуатационной нагрузке прогибы конца крыла могут составлять 5 – 10% его размаха.