Депланация сечений при сдвиге-кручении. Учёт конусности крыла, страница 2

9.2. Деформации кручения крыла. Относительный угол кручения (закручивания) крыла, определяется следующей зависимостью (см. рис. 3.28):

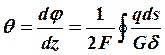,   где F – площадь, ограниченная одним из контуров сечения;

q – поток касательных усилий в элементах этого контура;

δ – толщина элементов контура (обшивки и стенок);

ds – элемент длины периметра контура;

- криволинейный интеграл берётся по длине контура сечения;

2F – удвоенная площадь контура.

G – модуль сдвига (модуль упругости второго рода).

Можно этот относительный угол закручивания определить и так:

    ()

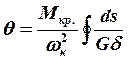При определении относительного угла кручения крыла интегрирование можно вести по одному из замкнутых контуров сечения. Объясняется это тем, что часто расположенные жёсткие в своей плоскости нервюры обеспечивают неизменяемость контура сечения крыла. Поэтому все контуры в сечении имеют одинаковые относительные углы кручения.

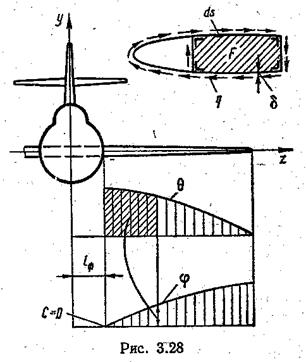
Интегрирование эпюры θ (рис. 3.28) даёт полный угол кручения:

,   где С – постоянная интегрирования, определяемая из следующего граничного условия: при z = l_ф угол кручения крыла у борта фюзеляжа равен нулю и С = 0.

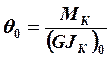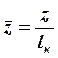Угол кручения тем больше, чем меньше площадь сечения крыла, ограниченная контуром, и чем больше величина крутящего момента. Приближённо угол кручения крыла можно определить. Полагая ,   где  - относительный угол кручения крыла у борта фюзеляжа;  - относительная координата. Тогда

.

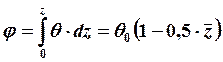При z = l_к   и φ = φ_max ≈ 0,5·θ₀·l_к

…………………………………………………………. (из уч. [В/М], стр. 114…115) ↓

Интегрирование производится численным способом или графически.

Найденные таким образом деформации не учитывают деформаций подфюзеляжной части крыла.

Рассчитывая деформацию стреловидного крыла, следует интегрирование вести вдоль его упругой оси, лежащей в плоскости изгиба.

При определении деформаций кручения нужно учитывать различие значений модуля сдвига G разных элементов крыла.

Рассмотрим некоторые особенности работы корневой части крыла.

При расчёте обычно принимают следующие допущения:

а) крыло (как и другие тонкостенные конструкции каркаса) работает на сдвиг и кручение в условиях свободной депланации сечений;

б) деформации, вызванные действием изгибающих моментов, сами по себе подчиняются закону плоских сечений и на депланацию сечений не влияют.

Эксперименты и теоретические исследования подтверждают справедливость этих допущений для концевой части крыла обычной конструкции.

Что касается корневой части крыла, то на её напряжённое состояние при упругой   работе крыла оказывает влияние стеснение депланаций, приводящее к возникновению в поперечных сечениях дополнительных нормальных напряжений при работе на сдвиг и кручение.

Это положение пояснено схемой на рис. 340, а. На схеме показаны дополнительные нормальные усилия в поясах, возникающие в заделке отсека крыла из-за стеснения депланаций, обусловленных кручением. В таких условиях полного стеснения депланаций находится при симметричной нагрузке крыла сечение крыла по плоскости симметрии самолёта.

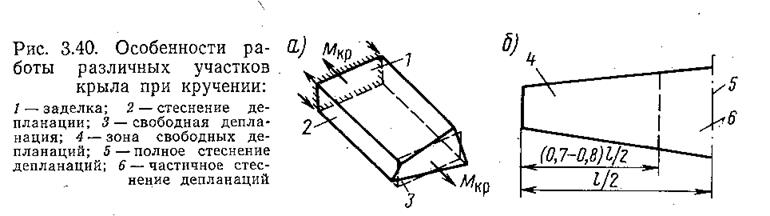Примыкающий участок крыла работает в условиях частичного стеснения депланаций (рис. 3.40, б).

Распределение усилий в элементах сечения крыла в зоне полного стеснения депланаций сходно с распределением усилий между болтами или заклёпками в узловом соединении, метод расчёта которого (метод центра жёсткости) предложении известным русским инженером В.Г.Шуховым. Метод расчёта крыла на стеснённое кручение разработан в 1932 г. В.Н. Беляевым.

Необходимо отметить, что при наступлении пластических деформаций указанные выше дополнительные напряжения в элементах корневой части крыла уменьшаются. На основании этого при расчётах на действие расчётной разрушающей нагрузки в случаях А и А′ можно приближённо не учитывать влияние стеснения депланаций и отклонений от закона плоских сечений.

Как показали исследования, при упругой работе конструкции стреловидного двухлонжеронного или моноблочного крыла вблизи корня возникают значительные дополнительные напряжения из-за отклонения деформаций изгиба от закона плоских сечений.

Эти дополнительные напряжения превышают по величине напряжения от стеснения депланаций настолько, что последними при расчёте стреловидного крыла можно пренебречь.

(Полностью расчёт деформаций при депланации сечений при сдвиге и кручении приводится в уч. Одинокова Ю.Г. Расчёт самолётов на прочность. Учебное пособие. 1973г.).