Функция и их производные. Построение графиков

Задание №1.

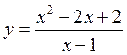
1. О.О.Ф.:

    D(y):

2.Функция чётная т.к.

                                     

3.  Функция не периодична.

4. Определение критических точек:

     

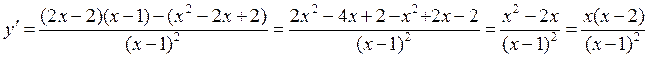
Подозрительные точки   x = 0,   x = 2,   x = 1  

y^’     +           -             -               +                 

y       

            0             1             2 

Т. к. при переходе через точку x = 0 функция меняет свой знак с «+» на «-», то точка х = 0 является точкой максимума (max), а при переходе через точку x = 2 функция меняет свой знак с «-» на «+», то точка х = 2 является точкой минимума (min).

Точка х = 1 – точка разрыва.

5. Найдём 2-ю производную:

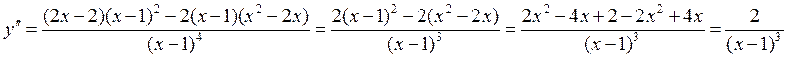
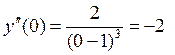 <  0, значит х = 0 – точка минимума (min).

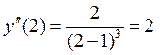>  0, значит х = 2 – точка максимума (max).

6. Участки выпуклости и вогнутости.

          -                   +

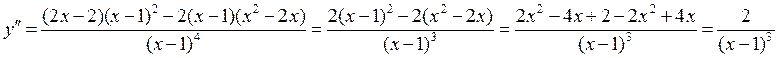
y                      1

При   -  график функции выпуклый вверх.

При  - график функции вогнутый вниз.

Точек перегиба нет.

7. Определение асимптот.

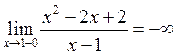
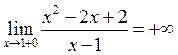
В точке х = 1 разрыв, т.е. – это вертикальная асимптота.

Найдём наклонную асимптоту    y=kx+b

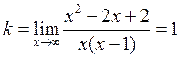
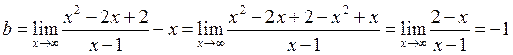
y = x – 1  -  наклонная асимптота.

8. Точки пересечения с осями координат:

                  с осью ОХ: у = 0 – нет пересечений.

                  с осью ОУ: х = 0 – у = - 2.

 9. Построение графика:

                                                                              Y

 

 

                                                                        0                                                            x

Задание №2.

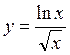
1. О.О.Ф.:

        D(y):

2. Функция чётная т. к.    

                                           

3.  Функция не является периодической.

4. Определение критических точек и интервалов монотонности:

                                                                    +             -

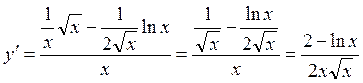
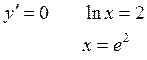
                                                        0                                      

Т. к. при переходе через точку x = е² функция меняет свой знак  с  «+»   на  «-»,   то   точка         х = е² является точкой максимума (max).

5. Найдём 2-ю производную:

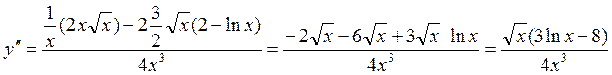
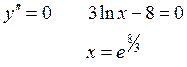
Участки выпуклости и вогнутости:

                                          -                   +

                             0                                               х

при - выпуклый вверх

при - вогнутый вниз

точка - точка перегиба

6. Найдём асимптоты:

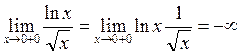
в точке  х = 0 -  вертикальная асимптота.

Найдём наклонную асимптоту   у = kx+b

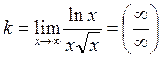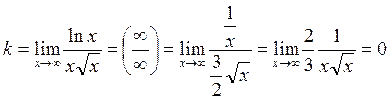
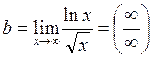, применим правило Лопиталя:

, применим правило Лопиталя:

y=0

7. Точки пересечения с осями координат:

                                           с осью ОХ: х = 1

                                           с осью ОУ пересечений нет.

8. Построение графиа:

                                                                              у

 

                                                                        0                                                                х

Задание 3.

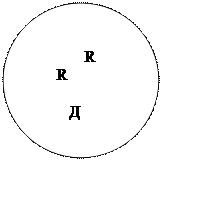
              На окружности дана точка А. Провести хорду ВС параллельно касательной в точке А, так чтобы площадь треугольника АВС была наибольшей.

Решение:

Т.к. ВС по условию      a , и т. к. АД       а => АД       ВС

                      А                      а                           Обозначим АД = Н

 

                                                                            Из треугольника ОВД по теорпме пифагора

                                                                            =

                                                                             =    

    В                                С                                   Получим

                                                                          

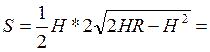
[ 0; 2R ]

         

                   

                   

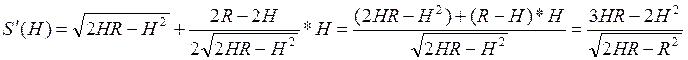
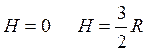
S(0)=0

S(2R)=

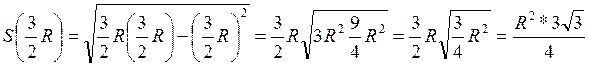
При 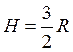 площадь будет наибольшей  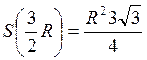чтобы провести хорду ВС, надо из точки А, провести перпендикулярно касательной отрезок равный , конец этого отрезка провести хорду параллельную касательной, получим ВС.