Исследование одномерных законов распределения случайных сигналов

Лабораторная работа №3

ИССЛЕДОВАНИЕ ОДНОМЕРНЫХ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ СИГНАЛОВ

Цель работы: Изучить и экспериментально исследовать одномерные функции распределения и плотности распределения вероятностей случайных сигналов.

Сведения из теории. Случайным процессом называется такая функция времени или какого-либо другого аргумента, значения которой заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью, меньшей единицы. Большинство сигналов, с которыми приходится встречаться на практике, носят в той или иной степени случайный характер.

Примером случайного процесса может служить флюктуационная помеха. Отдельно взятая реализация случайного процесса представляет собой некоторую конкретную функцию времени, полученную в результате одного опыта. Случайный процесс определяется всей совокупностью (ансамблем случайных реализаций).

Предположим, что случайный процесс Х(t) является стационарным и эргодическим. Определение функции распределения вероятностей F(x) основано на измерении относительного времени пребывания мгновенных значений процесса ниже уровня х, а определение плотности вероятностей w(x) – на измерении относительного времени пребывания мгновенных значений процесса в достаточно малом интервале (х - , х + ).

У нормального случайного процесса (например, флюктуационной помехи):

;                                           (1)

,            (2)

Где m – математическое ожидание процесса; 𝛅²- дисперсия процесса (𝛅 – среднеквадратическое отклонение):

– функция Крампа, – интеграл вероятностей, .

Распределения вероятностей гармонического колебания X(t)=Acos(ωt+φ), где А и ω – постоянные величины, а начальная фаза φ – случайная величина, описываются выражениями:

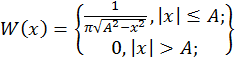                           (3)

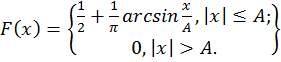                   (4)

Плотность распределения вероятностей огибающей суммы гармонического сигнала и стационарного центрированного гауссовского процесса с дисперсией

  (5)

Описывается выражением (1)

,         (6)

Где X(t) – центрированный гауссовский процесс с диспресией𝛅²и нулевым средним значением; I₀(x)– модифицированная функция Бесселя нулевого порядка.

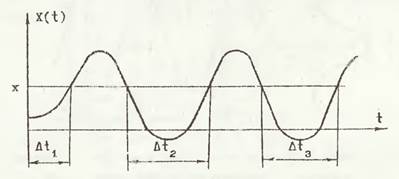
Рисунок 1 – График случайного процесса X(t) для определения функции распределения вероятностей.

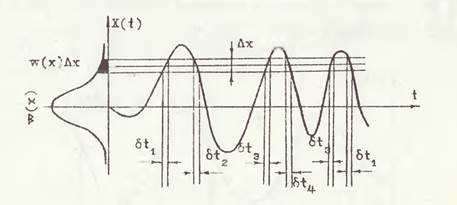
Рисунок 2 – График случайного процесса X(t) для определения плотности вероятности.